3.4 Обход по куче
Мы разобрали основные алгоритмы, однако я приведу ещё один алгоритм: обход по куче. Этот алгоритм необходим для утилизации кучи и для выполнения некоторых функций, например, получение указателей на все вершины.
Обход по куче будем выполнять по аналогии с обходом деревьев рекурсивной процедурой:
Обойти сына
Обойти партнера
Обойти соседа
Выполнить функцию
На сына идем при условии, что он присутствует. На партнера при условии, что он непомеченный (так как мы начинаем обход из корневой вершины, то в первую очередь приходим на помеченного соседа, поэтому рекурсию будем запускать только для непомеченного). С обходом соседа все несколько сложнее. Так как соседи образуют циклическое кольцо, необходимо сначала выделить это кольцо, а затем выполнить обход из каждой вершины кольца. Затем выполнить функцию и для самих элементов кольца.
В завершении шага рекурсии выполняем функцию для текущей вершины при условии, что она не равна вершине захода. Вершина захода устанавливается, когда мы обходим циклическое кольцо соседей для того, чтобы к корню не применялась функция до того, пока не обойдутся все элементы поддерева. Если этого не делать, то при вызове деструктора (деструктор в нашем случае вызывает обход, удаляя каждый элемент) корень дерева удалиться раньше, чем элементы, что приведет к утечке памяти.
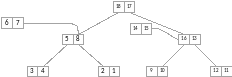
Рисунок 3.12: Пример обхода дерева кучи (вершины помечены в порядке обхода)
4 Сравнительный анализ очередей с приоритетом
Сравнение рассмотренных выше куч приведено в таблице
|
Бинарная куча |
Биномиальная куча |
Фибоначчиева куча |
2-3 куча |
Вставка |
Θ (log n) |
O(log n) |
Θ (1) |
Θ (1) |
Извлечение приоритетного |
Θ (log n) |
Θ (log n) |
O(log n) |
O (log n) |
Поиск приоритетного |
O(1) |
O (1) |
Θ (1) |
Θ (1) |
Изменение ключа |
Θ (log n) |
Θ (log n) |
Θ (1) |
Θ (1) |
Слияние |
Θ (n) |
Ω (log n) |
Θ (1) |
Θ (1) |
Достоинства |
1) Простота реализации 2) Требуют меньше всего памяти |
1) Все операции кроме поиска выполняются за логарифмическое время |
1) Все операции кроме тех, что требуют удаления выполняются за константное время |
1) Все операции кроме тех, что требуют удаления выполняются за константное время |
Недостатки |
|
|
|
|
Таблица 3: Сравнительный анализ рассмотренных куч
В алгоритмах на графах операция слияния как правило не используется, значит биномиальную кучу из дальнейшего сравнения можно исключить. Куча Фибоначчи и 2-3 куча становятся основными соперниками в дальнейшем сравнениями. Бинарная куча также будет присутствовать в сравнении чтобы можно было оценить необходимость использования более тяжелых структур данных.
Анализ производился на машине со следующими характеристиками:
ОС: Windows 7 Максимальная SP1
Процессор: Intel Pentium CPU 2030M 2x2.50GHz
Тип системы: 32-разрядная
Среда разработки и тестирования: Visual Studio Ultimate 2013.
В качестве бинарной кучи будем использовать std::priority_queue из библиотеки шаблонов C++. Фибоначчиева куча и 2-3 куча были реализованы мной.
Важной характеристикой является расход памяти, поэтому сделаем сравнение расходуемой памяти при различных размерах куч
Рисунок 4.1: Анализ занимаемой памяти.
Видно, что Бинарная куча занимает на порядок меньше памяти чем другие кучи. Хуже всего показала себя Фибоначчиева куча (приблизительно на 10% хуже, чем 2-3 куча).
Далее сравним предельные случаи операций вставки-удаления, поскольку это наиболее используемые операции.
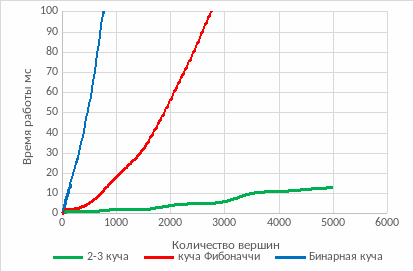
Рисунок 4.2 - Зависимость времени выполнения вставки-удаления от количества вершин (вставка N вершин,затем удаление)
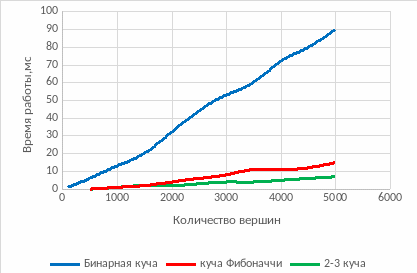
Рисунок 4.3 - Зависимость времени выполнения вставки-удаления от количества вершин (N раз вставка-удаление по одной вершине)
Видно, что при 2000 в первом случае 2-3 куча отработала в 2 раза медленнее чем во втором. Куча Фибоначчи отработала в 9 раз медленнее. Бинарная куча отработала на порядок хуже. По данному тесту 2-3 куча показала наилучший показатель быстродействия. Следовательно, 2-3 куча меньше всего зависит от режима поступления операций.