3.1 Вставка в кучу

Теперь рассмотрим основные операции над кучей, и начнем с операции вставки. Операция вставки определяется как слияние исходной кучи с кучей из одного дерева (если вставляем один элемент, то дерева 0f). В куче не может существовать два дерева одинаковой степени, поэтому пря появлении таковых мы будем их объединять до тех пор, пока все степени не будут различны. Может возникнуть две ситуации при слиянии куч: В самом простом случае при добавлении в кучу дерева может оказаться, что ячейка массива свободна, тогда просто занимаем её. В противном случае, если ячейка уже занята, будем производить слияние. (Рисунок 3.4)

Рисунок 3.4: Схема вставки в кучу

Слияние через партнера возникает, когда оба дерева ненасыщенные. В таком случае, раз оба дерева не имеют партнера, для объединения их достаточно просто связать их как партнеров. Операцию можно выразить формулой: nf + nf = nt (Рисунок 3.5)

Рисунок 3.5: Вставка через партнера

Слияние через сына выглядит несколько сложнее. В самом примитивном варианте, когда деревья степени 0, это выглядит так: из двух корневых элементов выбирается самый приоритетный (в случае если он из насыщенного дерева, мы его меняем местами с корневым элементом из ненасыщенного дерева), к нему добавляет насыщенное дерево как сына. При этом, раз степень дерева увеличилась, его необходимо вставлять заново (так как n+1 ячейка может быть занята). Общая формула: nf + nt = (n+1)f

Рисунок 3.6: Вставка через сына

Но тут возникает одна проблема, а что если деревья не нулевой степени (у каждого из деревьев уже есть сын)? В этом случае нам и пригодиться соседская связь. Мы отделяем сына от самого приоритетного элемента, и добавляем его как соседа к самому приоритетному из насыщенного дерева (помеченное как sl). Данная манипуляция представлена на рисунке 3.7 (на примерах 1f + 1t = 2f и 2f+2t = 3f):

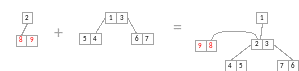
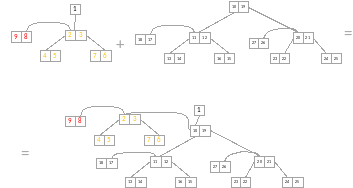
Рисунок 3.7: Пример использования соседской связи

К слову о соседских связях: использование левого соседа было описано выше, зачем же тогда правый сосед? Правый сосед используется как обратная связь, зацикливая переходы через соседей.

Например, для 3f дерева из примера выше самая верхняя соседская связь будет выглядеть так:

10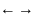 8 3 10. На схеме эти ссылки не указывались, во-первых, чтобы не усложнять рисунок, во-вторых наличие таких связей не обязательно, а лишь элемент моей реализации, который оптимизирует некоторые операции, например, это упрощает рекурсию при обходе кучи, а наличие обратной связи и вовсе позволяет заменить рекурсию циклом в операции изменения ключа. Ещё несколько моментов, связанных с моей реализацией: если необходимо вставить не одно дерево, а несколько, деревья подаются не как массив, а как одно дерево. Для этого все деревья связываются через корневые вершины как соседи. Так как соседская связь корневой вершины всегда не занята, эта манипуляция допустима. Если дерево не имеет соседей, то указатели ссылаются не на NULL, а на само дерево. Благодаря этому становиться проще формировать кольцевые списки соседей.

Существует ещё одна разновидность слияния – делением. Деление применяется в том случае, когда необходимо объединить две насыщенные вершины. При операции вставки не существует такой ситуации, при которой эта операция необходима, однако, данная операция имеет место при удалении. Опишем алгоритм вставки в кучу делением.

Из двух корневых вершин выберем самую приоритетную, и отделим от соседней. Отделенную вершину будем объединять через сына с насыщенным деревом. Таким образом если мы имели два дерева nt, на выходе будем иметь nf + (n+1) f. После этих манипуляций nf дерево оставляем лежать в ячейке, а (n+1) f вставляем заново.

Рисунок 3.8: Вставка Делением

Рисунок 3.9: Пример слияния 2t + 2t = 2f 3f

Теперь, когда все операции рассмотрены, самое время поговорить о реализации. Вставка будет разделена на два блока: интерфейс вставки и слияние. Интерфейс вставки будет отвечать за выборку двух сливаемых деревьев (вставляемое дерево + дерево, занимающее позицию), и обработку результата модуля слияния. В случае, когда позиция свободна модуль будет размещать дерево в нужной ячейке, в обратном же случае он будет отдавать управление модулю слияния. Модуль слияния отвечает за выбор алгоритма слияния, и приведение его в исполнение. На выход будут отдаваться ссылки на вставленное дерево (если нету, то NULL), и дерево, которое необходимо вставить (если нету, то NULL). Второй случай возникает тогда, когда в результате слияния степень дерева изменилась. Вставка через партнера возвращает вставленное дерево. Вставка через сына возвращает дерево, которое необходимо вставить. Вставка слиянием возвращает два дерева.

Вставка не зависит от количества элементов в куче, а зависит от количества деревьев. Но поскольку количество деревьев в куче в данный момент времени не зависит от количества элементов, то операция вставки не зависит от размера кучи, следовательно, операция работает за O(1).