2.2.1 Бинарная куча

Бинарные кучи также называют частично упорядоченными деревьями, поскольку порядок задается только между родителями и детьми, в тоже время как порядок между братьями или другими вершинами может быть выбран произвольно. Пример кучи, построенной на бинарном дереве предоставлен на рисунке 2.4

Рисунок 2.4 – Бинарная куча

Бинарную кучу обычно представляют и реализуют в виде массива. Такой выбор обусловлен тем, что куча сбалансирована, поэтому представление её как массива является тривиальной задачей. Хранение данных в виде массива, очевидно, экономнее, нежели в виде древовидной структуры. Применяется следующее правило для представления кучи в виде массива : если родительская вершина имеет индекс i, то её сыновья имеют индексы 2*i + 1 и 2*i + 2 соответственно ( при индексации с нуля).

Тогда куча на рисунке выше будет выглядеть следующим образом

100 19 36 17 3 25 1 2 7

Для вставки в бинарную кучу применяют следующий механизм:

Помещаем вершину в конец массива, потом сравниваем с родителем. Если родитель менее приоритетный, меняемся с ним местами. Производим данную процедуру до тех пор, пока не восстановим свойства кучи. Этот механизм называется просеивание вверх.

В качестве примера вставим в кучу вершину 43

100 19 36 17 3 25 1 2 7 43 = 100 19 36 17 43 25 1 2 7 3 = 100 43 36 17 19 25 1 2 7 3

Для изменения ключа модифицируем его значение на нужное, после чего при помощи просеивания восстанавливаем свойства кучи. Например, поменяем значение ключа 100 на 14

14 43 36 17 19 25 1 2 7 3 = 43 14 36 17 19 25 1 2 7 3 = 43 25 36 17 19 14 1 2 7 3

Для удаления ключа заменим первый элемент последним, после чего восстановим свойства кучи. Пример:

43 25 36 17 19 14 1 2 7 3 = 3 25 36 17 19 14 1 2 7 = 36 25 3 17 19 14 1 2 7 = 36 25 14 17 19 3 1 2 7

Одной из основных проблем бинарной кучи является отсутствие эффективного алгоритма для слияния куч. В бинарных кучах в качестве слияния можно использовать последовательное добавление всех элементов из кучи b в кучу a.

Следующая куча, которая будет рассмотрена, имеет эффективный алгоритм объединения.

2.2.2 Биномиальная куча

Биномиальная куча - это множество биномиальных деревьев, каждое из которых удовлетворяет свойству кучи (рисунок 2.6).

Биномиальное дерево — это дерево, определяемое по индукции:

B₀ – дерево, состоящее из одного узла.

B_i – дерево, состоящее из двух биномиальных деревьев B_i-1

Если рассмотреть дерево степени n, то на i уровне будет 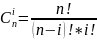вершин. Обычно биномиальные деревья представляются в виде корневого списка в порядке возрастания степеней (Рисунок 2.5)

Рисунок 2.5: Пример биномиальных деревьев

Рисунок 2.6: Пример биномиальной кучи

Для поиска приоритетного элемента достаточно пройти по всем корневым вершинам, и выбрать приоритетное. (Также можно хранить указатель на приоритетную вершины)

Для слияние куч мы сперва объединяем два дерева в одно, при этом вершины должны следовать в порядке возрастания степеней. Деревья одинаковых степеней мы сливаем между собой. Процесс соответствует двоичному сложению, то есть сложение двух деревьев степени n даст дерево степени n+1.

Пример сложения степеней:

1-2-3-5 + 2-3-4 = 1-2-2-3-3-4-5 = 1-3-3-3-4-5 = 1-3-4-4-5 = 1-3-5-5 = 1-3-6

Данная операция корректна, так как согласно структуре Бинома Ньютона дерево степени n имеет 2ⁿ вершин, а 2ⁿ + 2ⁿ = 2ⁿ⁺¹

Таким образом добавление элемента в кучу можно определить, как слияние текущей кучи с кучей из одного элемента (куча степени 0)

Для удаления из кучи приоритетного элемента необходимо сперва найти такой элемент, затем удалить из дерева корневой элемент. В результате дерево степени n распадется на деревья степеней 0,1 .. n-1. Доказать этот факт можно при помощи тождества

2ⁿ – 1 = 2^n-1 + 2^n-1 – 1

2^n-1 – 1 = 2^n-2 + 2^n-2 – 1.

…

2¹ – 1 = 2⁰ + 2⁰ – 1 = 2⁰

Значит 2ⁿ -1 =

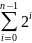
Для уменьшения ключа присваиваем ему новое значение, после чего при помощи просеивания поднимаем его вверх до тех пор, пока не восстановим свойства кучи.

Биномиальная куча дает логарифмическое время для всех основных операций. Однако не смотря на это данная куча не очень популярна. Это вызвано тем, что существуют кучи, которые работают быстрее при тех же затратах памяти (Бинарная куча, например, используется благодаря экономному расходу памяти, простоты реализации, и представления). Следующая куча, которая будет рассмотрена, является модернизированной версии биномиальной кучи, и ускоряет скорость работы некоторых операция до константных.