МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Учреждение образования

«Брестский государственный технический университет»

Республиканский конкурс научных работ студентов

высших учебных заведений Республики Беларусь

Информатика и информационные технологии. Программное обеспечение вычислительной техники и автоматизированных систем. Методы искусственного интеллекта

ОПТИМИЗАЦИЯ АЛГОРИТМОВ НА ГРАФАХ С ПОМОЩЬЮ 2-3 КУЧИ

Выполнил:

Наливко Денис Викторович

Студент 3 курса

Руководитель:

Глущенко Татьяна Александровна

Старший преподаватель

Брест,2016

Реферат

Работа 37 с., 5 ч., 38 рис., 3 табл., 4 источников

ОПТИМИЗАЦИЯ АЛГОРИТМОВ НА ГРАФАХ С ПОМОЩЬЮ 2-3 КУЧИ

Объектом исследования являются структуры для реализации очередей с приоритетом.

Цель работы – Сравнительный анализ наиболее часто используемых структур, данных для работы с очередями с приоритетом. Реализация эффективной структуры данных для работы с очередями с приоритетом и применение этой структуры данных для оптимизации алгоритмов на графах.

В процессе работы были сравнены наиболее используемые реализации очередей с приоритетом. Сравнение проводилось как по скорости выполнения операций, так и по скорости работы оптимизированных алгоритмов. В результате были сделаны выводы о необходимости использования тех или иных реализаций очередей с приоритетом.

Исследования в данной работе показали, что структура данных 2-3 куча является наилучшей реализацией очередей с приоритетом для оптимизации алгоритмов на графах.

СОДЕРЖАНИЕ

Введение

В компьютерных науках и программировании в целом очень важны быстродействие алгоритмов и их надежность, а если излагаться конкретнее, то необходимы оптимизации, которые ведут к ускорению работы алгоритма, уменьшению требования к ресурсам и при этом сохраняя уровень надежности на должном уровне. Вопрос оптимизации алгоритмов очень многогранен, поэтому целью моей работы будет оптимизация алгоритмов на графах, а точнее оптимизация определенного класса задач на графах. Оптимизация, изложенная в этой работе будет существенно ускорять выбор из множества (например, выбор ближайшего города в алгоритме Дейкстры для поиска кратчайшего пути). В этой работе будут кратко описаны некоторые родственные понятия, но описаны они будут на минимальном уровне, чтобы обеспечивать связь между понятиями. Далее будут рассмотрены основные подходы к реализации очередей с приоритетом, описание 2-3 кучи, сравнительный анализ.

1. Задачи на графах

Графы повсеместно используются в информатике для задач, связанных с взаимным расположением объектов, или сводимым к ним задач.

Приведем пример задач, которые решаются на графах:

• Поиск кратчайшего пути между парой вершин

• Поиск Гамильтонова цикла минимального веса в графе.

• Поиск минимального ациклического подграфа, которые включает в себя все вершины (поиск минимального остового дерева).

Мною не случайно были выбраны именно эти алгоритмы. Дело в том, что решение каждой из этих задач подразумевает выбор из множества некоторого самого оптимального решения для следующей итерации.

Например, для первой задачи можно использовать алгоритм Дейкстры и тогда нам будет необходимо на каждой итерации выбирать вершину, которая не была выбрана и ближе всего к начальной.

Для второй задачи (задача Коммивояжера) необходимо определять кратчайший путь между текущей вершиной, и множеством ещё не пройденных вершин при решении задачи алгоритмом выбора ближайшего соседа.

Для последней задачи можно использовать алгоритм Прима, где также необходимо получать минимальные пути от любой вершины из множества выбранных, до ближайшей из множества не выбранных.

Эти задачи (в которых необходимо выбирать оптимальное значение из множества) мы отнесем в отдельный класс. Данная работа направлена на оптимизацию именно этого класса задач на графах.

В каждом случае при решении в лоб мы должны на каждой итерации дополнительно тратить n итераций для определения минимума. Было бы не плохо иметь структуру данных, которая позволила бы получать значение минимума быстрее чем за линейное время (в идеале за константное). И в этом нам помогут очереди, а точнее очереди с приоритетом.

2. Очереди. Очереди с приоритетом.

Повседневно мы часто сталкиваемся с понятием очереди. Покупки в магазине, пробки, ожидание ответа от интернет ресурса – все это так или иначе связано с очередями.

Очередь – абстрактный тип данных с правилам доступа к элементам по принципу «первый пришёл — первый вышел» (FIFO, first-in-first-out). В соответствии с этим принципом у очереди есть начало (точка, откуда происходит удаление) и конец (точка, куда добавляются вершины).

Однако не всегда порядок выхода зависит от порядка входа. В этом случае говорят об очередях с приоритетом. Очередь с приоритетом — абстрактный тип данных, поддерживающий две обязательные операции — добавить элемент и извлечь приоритетный. Предполагается, что для каждого элемента можно вычислить его приоритет — действительное число или в общем случае элемент линейно упорядоченного множества. Очередь с приоритетом для множества элементов из A и заданной функцией 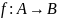представляет собой абстрактный тип данных, в котором элементы расположены согласно приоритету элементов.

Приоритет элемента — это некоторая числовая характеристика, описывающая важность элемента множества относительно других. В общем случае приоритет может задаваться как отображение x y,

где x – идентификатор элемента (значение)

y – Приоритет элемента (ключ).

Порядок следования элементов можно задавать при помощи логической функции f (x, y) которая вернет ИСТИНА если x приоритетнее y, и ЛОЖЬ в противном случае (функция приоритетности).

Таким образом очередь может быть реализована внутри очереди с приоритетом.

Примером очереди с приоритетом может быть очередь на игровой сервер с vip системой, очередь в поликлинику по талонам (Человек может прийти последним, но по талону на данное время, и тогда он пройдет первым) и т.д.