Расчет интерференционной картины от двух когерентных источников а) получение когерентных пучков делением волнового фронта

Для наблюдения интерференции света от реальных (некогерент- ных) источников необходимо свет от одного и того же источника раз- делить на два пучка (или несколько пучков) и затем свести эти пучки вместе. Способов разделения волны от первичного источника на две когерентные между собой волны два: 1) деление волнового фронта (метод Юнга, зеркала Френеля и т. д.) и 2) деление амплитуды (интерференция в тонких пленках). Метод получения когерентных пучков делением волнового фронта (он пригоден только для достаточно малых источников) заключается в том, что исходящий из источника пучок делится на два, а при наложении их друг на друга разность хода между интерферирующими лучами должна быть меньше длины когерентности.

Метод Юнга

Рис. 1.4

Роль вторичных когерентных источников S₁ и S₂ играют две уз- кие щели, освещаемые одним источником малого углового размера S. В более поздних опытах свет пропускался через узкую щель S, равно- удаленную от двух других щелей. Интерференционная картина на- блюдается в области перекрытия (тонированная область BC на левом рисунке) световых пучков, исходящих из S₁ и S_2.

Расчет интерференционной картины от двух когерентных источников

Две узкие щели S₁ и S₂ расположены близко друг к другу и яв-ляются когерентными источниками – реальными или мнимыми изо-бражениями источника в какой-то оптической системе. Результат ин-терференции – в некоторой точке P экрана, параллельного обеим щелям и расположенного от них на расстоянии l (l ≈ d). Начало от-

счета выбрано в точке О, симметричной относительно щелей. Интен-сивность в любой точке экрана, лежащей на расстоянии x от О, опре-деляется оптической разностью хода:

D = s₂ - s_1.

Из рис. 1.5получаем:

= + ; = + ;

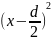- =2xd; D= - =2xd/( + );

=> + ≈2l => D=xd / l.

Из уравнений:

D = xd / l ,

D = ±ml₀

• условие интерференционных максимумов,

D = ±(2m + 1)l₀ / 2

• условие интерференционных минимумов,

(m = 0, 1, 2,…; l₀

находим:

– длина волны в вакууме)

– положение максимумов интенсивности

2.Интерференция света в тонких пленках. Полосы равного наклона и равной толщины. Кольца Ньютона. Интерференция света в тонких пленках

Рис. 1.6

Лучи 1 и 2, идущие от S к Р (точка Р на экране, расположенном в фокальной плоскости линзы), порождены одним падающим лучом и после отражения от верхней и нижней поверхностей пластинки параллельны друг другу. Если оптическая разность хода лучей 1 и 2 мала по сравнению с длиной когерентности падающей волны, то они когерентны, а интерференционная картина определяется оптической разностью хода между интерферирующими лучами.

Оптическая разность хода между интерферирующими лучами от точки О до плоскости АВ:

l

D = n (OC + CB) - OA ± ⁰ ,

2

OC = CB = ^d , n (OC + CB) =

cos r

OA = OB sin i = 2d tg r sin i .

2 nd _, cos

Учитывая закон преломления света sin i / sin r = n / n₀ = n , получим

_

_

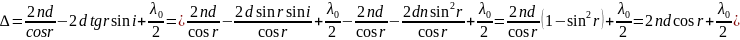
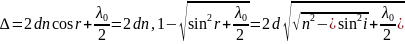
Здесь n – показатель преломления пленки; d – толщина плоскопараллельной пластинки; i – угол падения; r – угол преломления; ₀ – длина волны в вакууме, член + /2, обусловлен потерей полуволны при отражении света от границы раздела. При n  n₀ потеря полуволны в точке О и /2

Будет иметь знак минус, при n  n₀– в точке С и /2 надо брать с плюсом;

m – порядок интерференции.

;