5. Смешанное произведение векторов

Определение: Смешанным произведением трех векторов , , называется число, равное скалярному произведению вектора на векторное произведение векторов х , т. е.

( х )

Теорема (геометрический смысл смешанного произведения). Смешанное произведение ( х ) равно объему v параллелепипеда, построенного на векторах , , , взятому со знаком «+», если тройка , , - правая, со знаком «-», если тройка , , -левая. Если же , , - компланарны, то ( х )=0.

Другими словами: ( х )=

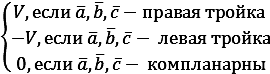
Свойства смешенного произведения

1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. ( х ) =( 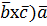= ( х

2. Смешенное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т. е. х = ( х )

3. Смешенное произведение меняет свой знак при перемене мест любых двух векторов – сомножителей, т. е. =- , =- , =-

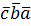
4. Смешанное произведение ненулевых векторов , , равно нулю, тогда и только тогда, когда они компланарны

Выражение смешанного произведения через координаты

Теорема: Если векторы , , заданы своими координатами = {x₁, y_1, z₁}, ={x₂, y_2, z₂}, ={x₃, y_3, z₃}, то смешанное произведение , , определяется формулой = – разложение определителя третьего порядка по элементам третьей строки

Таким, образом, смешанное произведение векторов равно определителю третьего порядка, составленного из координат перемножаемых векторов.

Приложения смешанного произведения

1. Определение взаимной ориентации векторов , , следует из:

   • если >0, то - правая тройка,

   • если <0, то 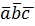-левая тройка

2. Векторы , , компланарны тогда и только тогда, когда их смешанное произведение равно нулю ( ≠0, , )

компланарны.

3. Объем параллелепипеда, построенного на векторах , вычисляется по формуле V= , объем треугольной пирамиды, построенной на этих же векторах, равен V=

Лекция № 4. Тема: Линейные пространства, базис. Линейные преобразования.

План:

1. Понятие линейного пространства.

2. Исследование системы векторов на линейную зависимость и линейную независимость.

3. Базис пространства.

4.Отыскание собственных векторов и собственных значений линейного преобразования.

1. Понятие линейного пространства.

Определение. Линейным пространством называется совокупность (множество) элементов (объектов) , в котором задано правило, ставящее в соответствие каждым двум элементам некоторый третий элемент, называемый их суммой: , и указано правило, ставящее в соответствие каждому элементу и каждому числу некоторый новый элемент этой же совокупности, называемый их произведением: .

При этом выполняются следующие условия (аксиомы):

1) – коммутативности;

2) – ассоциативности;

3) существования в пространстве нейтрального (нулевого) элемента , от прибавления которого никакой вектор не изменяется:

;

4) существования в пространстве для каждого элемента элемента , противоположного ему, такого, что в сумме они дают нулевой элемент : ;

5) ;

6) – ассоциативность относительно умножения на число;

7) – дистрибутивность относительно сложения чисел;

8) – дистрибутивность относительно сложения элементов.

Определение: Линейное пространство называется векторным пространством. Элементы векторного пространства называются векторами.

Если действие умножения на числа определено только на множестве вещественных чисел , то векторное пространство называется вещественным; если – на множестве всех комплексных чисел , то –комплексным векторным пространством.

Примеры линейных пространств:

1. Совокупность многочленов всех степеней с комплексными коэффициентами: образует линейное пространство. -элементом здесь является многочлен, у которого все коэффициенты нуль; противоположным элементом является многочлен, у которого все коэффициенты те же, что у исходного, но с противоположным знаком. Легко проверить выполнение и всех остальных аксиом.

2. Легко убедиться, что совокупность многочленов, степени , также является линейным пространством. Однако совокупность многочленов степени уже не является линейным пространством. Сумма таких многочленов может вывести за пределы этого множества; оно не содержит - элемента.

Следствия из аксиом:

1. единственность - элемента.

2. единственность противоположного элемента.

3. умножение любого вектора на число нуль дает -элемент.

4. умножение любого вектора на число дает противоположный элемент.