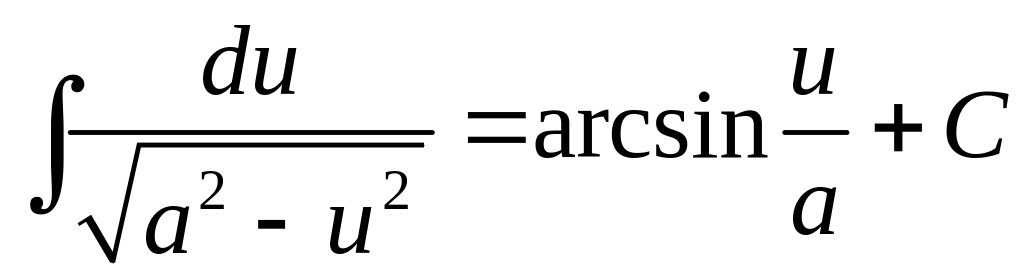- •Е.Ю. Романова математика
- •Лекция № 1 Тема: Матрицы и определители.
- •1. Понятие матрицы. Виды Матриц.
- •2. Действия над матрицами
- •3. Виды определителей и правила их вычисления.
- •4. Минор, алгебраическое дополнение.
- •5. Свойства определителей:
- •6. Обратная матрица
- •7. Ранг матрицы.
- •Лекция №2 Тема: Решение систем линейных уравнений
- •1. Общие понятия системы линейных уравнений.
- •2.Формулы Крамера.
- •3. Метод обратной матрицы.
- •4.Метод Гаусса.
- •Лекция № 3. Тема: Векторы. Скалярное, векторное и смешанное произведение векторов
- •1. Понятие вектора. Коллинарность, ортогональность и компланарность векторов.
- •2. Линейные операции над векторами:
- •3. Скалярное произведение векторов
- •4. Векторное произведение векторов
- •5. Смешанное произведение векторов
- •Лекция № 4. Тема: Линейные пространства, базис. Линейные преобразования.
- •1. Понятие линейного пространства.
- •2. Исследование системы векторов на линейную зависимость и линейную независимость.
- •3. Базис пространства.
- •4. Отыскание собственных векторов и собственных значений линейного преобразования
- •Лекция № 5. Тема: Квадратичные формы
- •1. Запись квадратичной формы в матричном виде
- •2. Приведение квадратичной формы к каноническому виду.
- •3. Исследование на положительную (отрицательную) определенность.
- •Лекция № 6. Тема: Прямая линия на плоскости
- •3. Гипербола
- •4. Парабола
- •Лекция № 8. Тема: Плоскость и прямая в пространстве
- •1. Виды уравнений плоскости в пространстве.
- •1.2. Уравнение в отрезках
- •1.3. Векторное и нормальное уравнение плоскости
- •1.4. Нормальное уравнение плоскости.
- •1.5. Взаимное расположение двух плоскостей
- •1.6.Уравнение плоскости, проходящей через три заданные точки
- •2. Виды уравнений прямой в пространстве.
- •2.1.Общие уравнения прямой
- •2.2. Параметрические и канонические уравнения прямой
- •2.3.Уравнения прямой, проходящей через две заданные точки
- •3. Условия параллельности и перпендикулярности прямых в пространстве.
- •4. Условия параллельности и перпендикулярности прямой и плоскости.
- •4.1.Условие параллельности прямой и плоскости.
- •4.2.Условие перпендикулярности прямой и плоскости.
- •2. Числовая последовательность.
- •3. Предел функции в точке.
- •4. Предел функции на бесконечности.
- •5. Основные теоремы о пределах.
- •6. Замечательные пределы.
- •Лекция № 10. Тема: Непрерывность функции. Классификация разрывов
- •1. Непрерывность функции.
- •2. Классификация точек разрыва
- •2. Основные правила дифференцирования.
- •3.Таблица производных
- •4. Производная сложной функции.
- •5. Производная обратной функции.
- •6. Понятие дифференциала функции. Дифференциал функции.
- •Лекция № 12. Тема: Применение производной и дифференциала.
- •1. Основные теоремы дифференциального исчисления
- •2. Применение производной к исследованию функции.
- •2.1. Интервалы возрастания и убывания функции.
- •2.2. Экстремумы функции.
- •2.3. Интервалы выпуклости и вогнутости графика функции
- •2.4. Асимптоты графика функции
- •2.5. Общая схема исследования функции и построение ее графика
- •Дифференциал функции.
- •2.Свойства неопределенного интеграла. Таблица интегралов.
- •3. Замена переменной в неопределенном интеграле
- •4. Интегрирование по частям в неопределенном интеграле.
- •5. Интегрирование рациональных дробей.
- •5. Интегрирование тригонометрических выражений.
- •Лекция № 14. Тема: Определённый интеграл.
- •1. Определенный интеграл и его свойства
- •Лекция № 15. Тема: Понятие функции нескольких переменных. Дифференциальное исчисление функции нескольких переменных.
- •1. Понятие функции нескольких переменных.
- •2. Частные производные функции нескольких переменных.
- •Лекция № 16. Тема: Дифференциальные уравнения 1-ого порядка.
- •1. Понятие дифференциального уравнения 1 – го порядка
- •2.Уравнения с разделяющимися переменными
- •3. Однородные дифференциальные уравнения первого порядка
- •4. Линейные дифференциальные уравнения первого порядка
- •5. Уравнение Бернулли.
- •Лекция № 17. Тема: Дифференциальные уравнения 2-ого порядка.
- •1. Понятие дифференциального уравнения 2-го порядка.
- •2. Уравнения 2-го порядка, допускающие понижение порядка.
- •3. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •4. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Лекция № 19. Тема: Числовые ряды
- •1. Основные понятия.
- •2. Признаки сходимости рядов.
- •3.Знакочередующиеся ряды. Знакопеременные ряды.
- •Тема: Степенные ряды.
- •1. Понятие степенного ряда.
- •2. Разложение функций в степенные ряды
Дифференциал функции.
Пусть функция
![]() определена в окрестности
определена в окрестности
![]() и имеет производную в этой точке
и имеет производную в этой точке
![]()
При этом
![]() .
Тогда для достаточно малых
.
Тогда для достаточно малых
![]() можно записать
можно записать
![]()
Причем
![]() при
при
![]() .
В этом случае приращение функции можно
записать в виде
.
В этом случае приращение функции можно
записать в виде
![]()
Или
![]()
Определение. Функция
называется дифференцируемой в точке
![]() , если ее приращение
, если ее приращение
![]() можно представить в виде
можно представить в виде![]()
где не зависит от , но вообще зависит от .
Теорема. Для того чтобы функция была дифференцируема в точке , необходимо и достаточно, чтобы она имела конечную производную в этой точке.
Таким образом, сказать, что имеет производную в точке или что дифференцируема в точке - это одно и то же. Поэтому процесс нахождения производной называют дифференцированием функции.
Доказательство.
Достаточность условия доказана выше:
из существования конечной производной
![]() следовала возможность представления
∆y в виде
,
где можно положить
следовала возможность представления
∆y в виде
,
где можно положить
![]() .
.
Необходимость. Пусть функция
дифференцируема в точке
.
Тогда, если
![]() ,
можно записать
,
можно записать
![]()
Предел левой части при
существует и равен
:![]()
Это означает, что существует производная
![]() .
.
3. Применение дифференциалов к приближенным вычислениям
По определению![]() .
Отсюда следует, что дифференциал функции
при достаточно малом
может служить хорошим приближением
приращения функции. В этом смысле пишут
приближенное равенство
.
Отсюда следует, что дифференциал функции
при достаточно малом
может служить хорошим приближением
приращения функции. В этом смысле пишут
приближенное равенство
![]()
где
![]() .
.
Пример. Вычислить значение
![]() .
Имеем
.
Имеем
![]() ,
,
![]() ,
,
![]() .
.
Далее
![]() .
Или
.
Или
![]() .
Окончательно
.
Окончательно
![]()
Лекция № 13.
Тема: Неопределённое интегрирование.
План:
Понятие неопределенного интеграла.
Свойства неопределенного интеграла. Таблица интегралов.
Замена переменной в неопределенном интеграле
Интегрирование по частям в неопределенном интеграле.
Интегрирование рациональных дробей.
Интегрирование тригонометрических выражений.
1. Понятие неопределенного интеграла.
Определение. Функция
![]() называется первообразной функции
называется первообразной функции
![]() заданной
на интервале
заданной
на интервале
![]() ,
если она дифференцируема
,
если она дифференцируема
![]() и для любого
из этого интервала
и для любого
из этого интервала
![]() .
.
Определение. Совокупность всех
первообразных функции
на интервале
называется неопределенным интегралом
от функции
и обозначается
![]() .
.
называется подынтегральной функцией,
![]() – подынтегральным выражением,
– переменной интегрирования.
– подынтегральным выражением,
– переменной интегрирования.
2.Свойства неопределенного интеграла. Таблица интегралов.
Пусть
![]() – одна из первообразных
.
– одна из первообразных
.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
Таблица интегралов:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|