МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ТВЕРСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ»
Е.Ю. Романова математика
Курс лекций
для студентов инженерного факультета
направлений подготовки 23.03.01, 23.03.03 и 35.03.06
Тверь
Тверская ГСХА
2016
Романова Е.Ю. Математика: курс лекций для студентов инженерного факультета направлений подготовки 23.03.01, 23.03.03 и 35.03.06 / М.Ю. Петров. – Тверь: Тверская ГСХА, 2016. – 83 с.
Курс лекций рассмотрен и утвержден на заседании предметно-методической комиссии кафедры ФМД и ИТ (протокол №1 от 12 сентября 2016 г.).
Курс лекций содержит научно-теоретические знания и освещает содержание дисциплины в соответствии с рабочей программой дисциплины «Информационные технологии в отрасли».
Курс лекций предназначен для студентов инженерного факультета направлений подготовки 23.03.01, 23.03.03 и 35.03.06.
Министерство сельского хозяйства Российской Федерации
ФГБОУ ВО Тверская ГСХА
Лекция № 1 Тема: Матрицы и определители.
План:
Понятие матрицы. Виды Матриц.
Действия над матрицами.
Виды определителей и правила их вычисления.
Минор, алгебраическое дополнение.
Свойства определителей.
Обратная матрица.
Ранг матрицы.
1. Понятие матрицы. Виды Матриц.
Определение. Матрицей размера m
n
называется таблица чисел, , содержащая
m строк и n
столбцов.
=
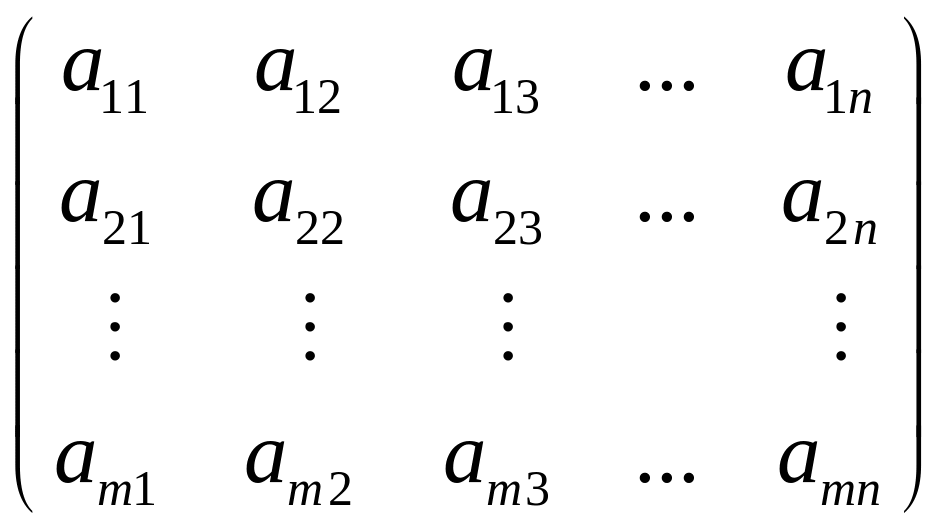или
=
,
=1,2,…,
,
1,2,…,
.
– элемент матрицы, стоящий на пересечении
-й
строки и
-го
столбца.
Определение. Если
,
то матрица называется квадратной
n-го порядка, в противном
случае – прямоугольной.
Элементы
,
= 1, 2, …, n квадратной
матрицы А образуют ее главную
диагональ.
Матрица размера 1хn
называется матрицей-строкой, а
матрица размера
– матрицей-столбцом.
Определение. Две матрицы называются равными, если они имеют одинаковый размер и равны их элементы, стоящие на одинаковых местах.
Определение. Квадратная матрица
называется диагональной, если равны
нулю все ее элементы, расположенные вне
главной диагонали, то есть
На главной диагонали могут быть любые
числа. Если все они равны 1, то диагональная
матрица называется единичной и
обозначается буквой
.
Определение. Квадратная матрица называется треугольной, если все ее элементы снизу (сверху) от главной диагонали равны нулю.
2. Действия над матрицами
Определение. Пусть
=
и
=
,
=1,2,…,
,
=1,2,…,
– матрицы размера
.
Матрица
=
также размера
называется суммой матриц
и
,
если
,
=1,2,…,
,
=1,2,…,
.
Пример.
=
,
=
=
Определение. Произведением
матрицы
=
размера
на число
называется матрица
=
того же размера, элементы которой
,
=1,2,…,
,
k=1,2,…,
.
Пример.
=
=
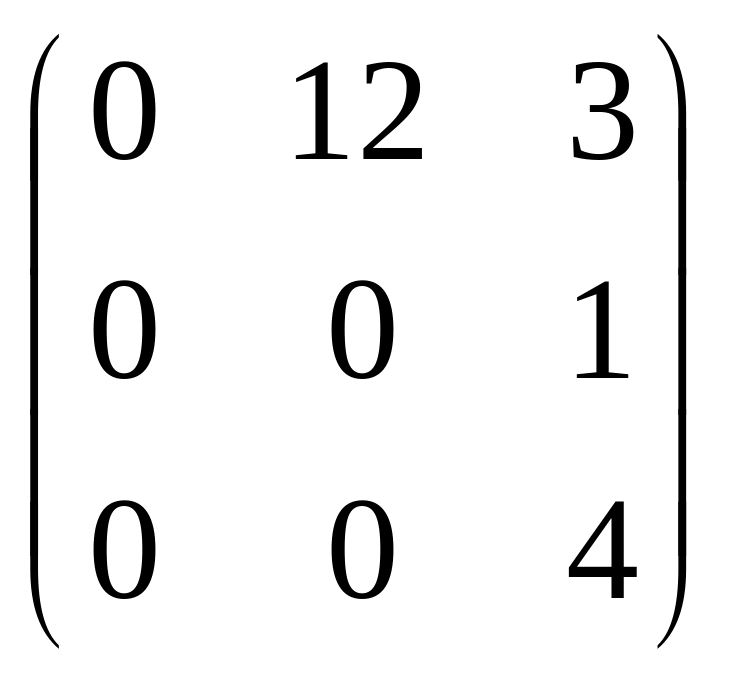
Определение. Нулевой матрицей
называется матрица, все элементы которой
равны нулю.
Определение. Матрица
называется противоположной для
и обозначается
.
Очевидно, что
для любой матрицы А.
Определение. Разностью матриц
и
одного размера называется сумма
и обозначается
.
Определение. Транспонированной
матрицей
для матрицы
размера
называется матрица размера
,
полученная из
заменой всех ее строк столбцами с теми
же порядковыми номерами.
То есть, если
=
,
то
,
=1,2,…,
,
=1,2,…,
.
Пример.
=
;
Определение. Если = , то матрица А называется симметрической.
Все диагональные матрицы симметрические, так как равны их элементы, симметричные относительно главной диагонали.
Справедливы следующие свойства операции транспонирования:
Определение. Пусть
=
– матрица размера
,
=
– матрица размера
.
Произведение этих матриц
– матрица
=
размера
,
элементы которой вычисляются по формуле:
,
=1,2,…,
,
=1,2,…,
,
то есть элемент
-й
строки и
-го
столбца матрицы
равен сумме произведений соответствующих
элементов
-й
строки матрицы
и
-го
столбца матрицы
.
Пример.
=
,
=
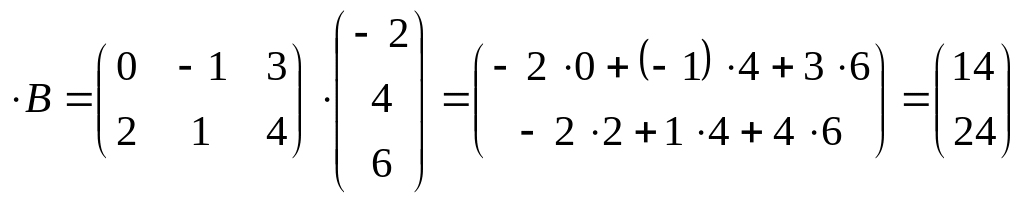
Произведение
– не существует.
Замечание. Элементами матрицы могут быть не только числа, но и функции. Такая матрица называется функциональной.
Пример.
