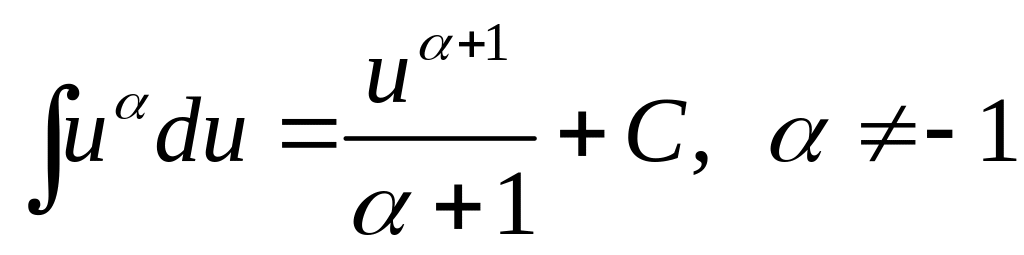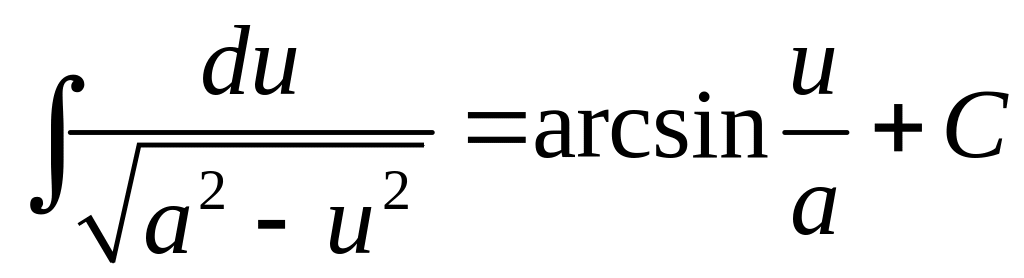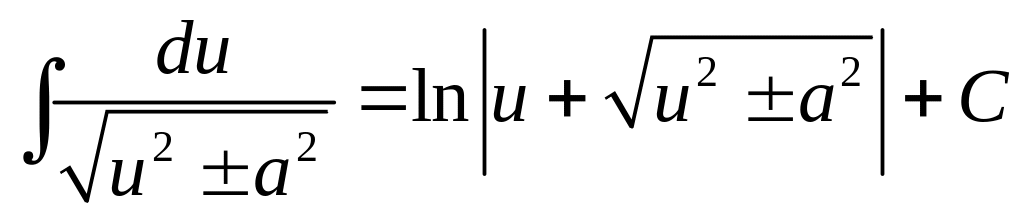5. Производная функции и дифференциал.
Дифференциал функции равен произведению производной на дифференциал аргумента независимо от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.
Например, дифференциал сложной функции.
Пример. Задана
функция
.
Найти
Задания для выполнения контрольной работы по теме 1.
Задание 1. Вычислить пределы (выбрать один вариант):
1 вариант |
а) |
б) |
2 вариант |
a) |
б)
|
3 вариант |
а) |
б) |
4 вариант |
а) |
б) |
5 вариант |
а) |
б) |
6 вариант |
а) |
б) |
7 вариант |
а) |
б) |
8 вариант |
а) |
б) |
9 вариант |
а) |
б) |
10 вариант |
а) |
б) |
Задание 2. Найти производные первого порядка данных функций, используя таблицу производных правила вычисления производных (выбрать один вариант):
1
вариант
а) y
=
б) y
=
в)
y
=
г) y
=
д) y
=
2
вариант
а) у =
б) у =
в)
у =
г) у =
д) у =
3
вариант
а)
б)
в)
г)
д)
4
вариант
а)
б)
в)
г)
д)
5
вариант
а)
б)
в)
г)
д)
6
вариант
а)
б)
в)
г)
д)
7
вариант
а)
б)
в)
г)
д)
8
вариант
а)
б)
в)
г)
д)
9
вариант
а)
б)
в)
г)
д)
10
вариант а)
б)
в)
г)
д)
Тема 2: неопределённое интегрирование. Определённый интеграл.
План:
Понятие неопределенного интеграла.
Свойства неопределенного интеграла. Таблица интегралов. Непосредственное интегрирование.
Основные методы интегрирования в неопределенном интеграле: замена переменной в неопределенном интеграле, интегрирование по частям в неопределенном интеграле, интегрирование рациональных дробей.
Определенный интеграл и его свойства. Формула Ньютона-Лейбница.
Основные методы интегрирования в определенном интеграле: замена переменной в неопределенном интеграле, интегрирование по частям в неопределенном интеграле.
1. Понятие неопределенного интеграла.
Определение.
Функция
называется первообразной функции
заданной
на интервале
,
если она дифференцируема
и для любого
из этого интервала
.
Определение.
Совокупность всех первообразных
функции
на интервале
называется неопределенным интегралом
от функции
и обозначается
.
называется
подынтегральной функцией,
– подынтегральным выражением,
– переменной интегрирования.
2.Свойства неопределенного интеграла. Таблица интегралов. Непосредственное интегрирование.
Свойства неопределенного интеграла.
Пусть
– одна из первообразных
.
1.
.
2.
.
3.
.
Таблица интегралов:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
Непосредственное интегрирование.
