Экономическая интерпретация взаимно-двойственных задач

Пусть предприятие выпускает видов продукции, используя видов сырья; - запас сырья -го вида, - расход сырья -го вида для производства единицы продукции -го вида, - прибыль от продажи единицы изделия -го вида, - количество единиц продукции -го вида, которое требуется выпускать .

Математические модели исходной и двойственной задачи выглядят следующим образом:

Задача 1	Задача 2

Пусть теперь предприятие решило прекратить производство изделий и продать ресурсы, идущие на их изготовление. Обозначим через цену единицы ресурсов i-го вида.  Цены на ресурсы должны удовлетворять следующим двум требованиям:

• общая стоимость ресурсов не должна быть слишком высокой, иначе их невозможно будет продать;

• сумма от реализации ресурсов должна быть больше прибыли от реализации готовой продукции.

Первое требование выражается условием

,

а второе– ограничениями

Действительно, выражение в левой части -го неравенства есть сумма от продажи ресурсов, идущих на изготовление j -го изделия, в правой части – прибыль от продажи единицы j-го изделия:

Вид сырья	Нормы расхода сырья на единицу продукции					Запас сырья
	1-го вида	…	-го вида	…	-го вида
		…		…
		…		…
…	…	…	…	…	…	…
		…		…
Прибыль		…		…

Таким образом, двойственная соответствует следующей экономической проблеме: по каким минимальным ценам следует продавать ресурсы, чтобы прибыль от их реализации была больше прибыли, полученной от реализации продукции, изготавливаемой с использованием этих ресурсов.

Значения переменных  называют теневыми ценами. Они показывают, насколько увеличится максимальная прибыль, при увеличении запасов соответствующего ресурса на единицу.

Действительно, пусть F* - максимальное значение прибыли в задаче о производстве. Если запасы ресурсов изменить, то может измениться и максимальная прибыль F*. Это означает, что F* является функцией от ресурсов , , т.е.

Рассмотрим отношение приращения максимальной прибыли  к приращению i-го ресурса

;

По определению частной производной

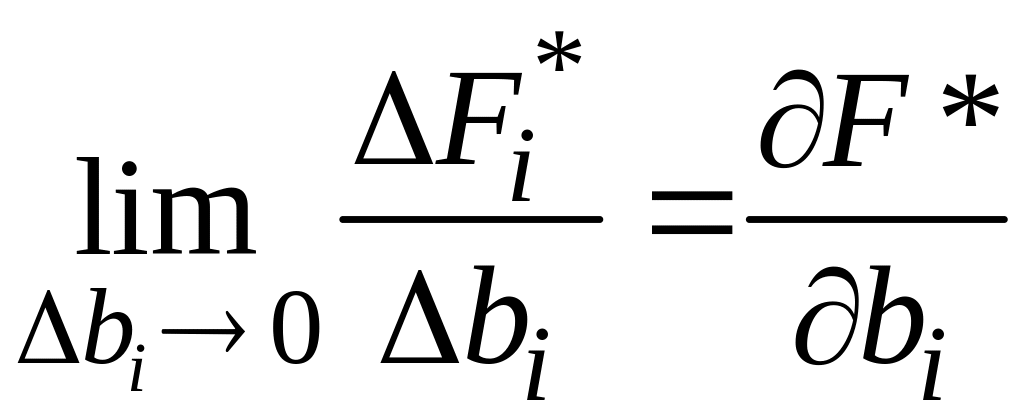
По первой теореме двойственности оптимальное значение целевой функции прямой задачи совпадает с оптимальным значением целевой функции двойственной задачи

тогда

Таким образом, оптимальное значение двойственной переменной  числено равно приращению максимальной прибыли  при увеличении   i-го ресурса на единицу ( ), если величина  является достаточно малой по сравнению с величиной