7. Антенны

7.6. Антенны свч диапазона

Антенны СВЧ диапазона относятся к классу апертурных антенн и антенн поверхностных волн.

К апертурным антеннам относятся волноводные, рупорные, рефлекторные (зеркальные, параболические), линзовые антенны, антенные решетки с электрическим сканированием, в которых излучение происходит через раскрыв, иначе называемый аперту­рой, площадью S_а. В таких антеннах отношение S_а /λ² можно получить очень большим. При больших значениях S_а /λ² КНД антенны достигает сотен тысяч – миллионов. Такая высокая направленность приближает апертурные антенны к оптическим системам, где также применяются рефлекторы и линзы.

Антеннами поверхностных волн называются антенны, состоящие из возбудителя бегущих электромагнитных волн и направителя, по поверхности которого эти волны распространятся с фазовой скоростью υ_ф, меньшей скорости света с. Иначе говоря, направитель является замедляющей структурой. Направители бывают диэлектрическими и металлическими. По форме направители антенн поверхностных волн могут быть плоскими, дисковыми и стер­жневыми. В качестве возбудителей чаще всего используют односторонне нап­равленные излучатели: рупор, открытый конец волновода, вибратор с рефлек­тором и т. д. Антенны поверхностных волн в своем подавляющем большинстве являют­ся антеннами бегущей волны.

Отличительной чертой антенн СВЧ диапазона является разделение процессов преобразования энергии токов высокой ча­стоты в энергию электромагнитных волн и процессов направленного излучения этих волн. Первую функцию в апертурной антенне выпол­няет облучатель, а вторую – рупор, линза, рефлектор, подобно тому, как в антенне поверхностных волн указанные функции выполняют со­ответственно возбудитель и направитель.

Особенностью апертурных антенн является параллельное возбуждение их элемен­тов, что способствует расширению по­лосы пропускания антенн, тогда как элементы антенны бегущей волны возбуждаются последовательно, один за другим.

7.6.1 Волноводные излучатели

В диапазоне сантиметровых волн находят применение антенны в виде открытого конца прямоугольного (рисунок 7.1) или круглого волновода.

Антенны этого типа является простейшей апертурной антенной (апертура  антенны – открытый конец волновода). Они используются самостоятельно, например, в качестве слабонаправленных антенн летательных аппаратов, а также в качестве элементов фазированных антенных решеток  и как облучатели более сложных антенн, например, линзовых и зеркальных.

Рисунок 7.1 – Волноводный излучатель

Распространяющаяся в волноводе волна Н₁₀, со­здаваемая вибраторным возбудителем дойдя до открытого конца, частично отражается обратно, а частично излучается. В месте перехода от волновода к открытому пространству, т. е. в раскрыве, возникают волны высших типов, а также появляются поверхностные токи на наружных стенках волновода.

Положим, что выходящие из этой апертуры волны не отражаются обратно, а токи проводимости не затекают с внутренней на внешнюю поверхность, волновода. В таких условиях фронт волны в раскрыве плоский. Это упрощает исследование излучения волновода, тем более, что в данном случае можно применить принцип Гюйгенса, согласно которому каждый элемент волноводного фронта возбуждает вторичные волны, из которых формируются электромагнитные волны во внешней среде. Отсюда происходит название элементарного излучателя такого вида - элемент Гюйгенса.

Направленные свойства волноводного излучателя рассматриваются в следующей по­следовательности: 1) определяется функция направленности элементарного излучателя (здесь это элемент Гюйгенса), 2) находится множитель направленности решетки, образованной элементами раскрыва в предположении, что каждый из них ненаправленный (изотропный), 3) определяется общая функция направленности апертуры как произведение функций, по­лученных на первых двух этапах исследования.

Поля излучения элемента Гюйгенса можно представить в виде суммы полей двух элементар­ных излучателей - электрического и магнитного диполей Герца.

Ось первого перпендикулярна вектору Н, а ось второго - вектору Е, и так как на плоском вoлновом фронте силовые линии электрического и магнитного полей взаимно перпендикулярны, то диполи находятся под прямым углом.

Выделим элемент Гюйгенса прямоугольной формы с равными сто­ронами dy, dz в середине отверстия прямоугольного волновода (рисунок 7.2, а) и определим функции направленности элемента: F₁(θ_b) в пло­скости zОх и F₂ (θ_а) в плоскости уОх.

Рисунок 7.2 - Раскрыв прямоугольного волновода с выделенным на нем

элементом Гюйгенса (а) и ДН этого элемента в плоскостях Е (б) и Н (в)

Оба диполя данного элемента со­здают электрические (и магнитные) поля с равной амплитудой в глав­ных направлениях, но так как диполи перпендикулярны, то их ДН по – разному ориентированы в пространстве.

Электрический диполь в Е-плоскости zОх (рисунок 7.2, б) обладает направленностью согласно уравнению F' (θ_b) = sin (θ_b) (штрихпунктирная линия), посколькy эта плоскость для него является меридио­нальной. Эта же плоскость для магнитного диполя является экваториальной, а потому в любом направлении плоскости zОх магнитный ди­поль создает одинаковое излучение: F" (θ_b) = 1 (штриховая линия). Результирующая ДН (сплошная линия) выражается уравнением кар­диоиды

f₁(θ_b)=F'(θ_b)+F_а(θ_b)=1+sinθa, (7.1)

Магнитная плоскость, наоборот, является экваториальной для электрического диполя и меридиональной для магнитного, следо­вательно, ДН электрического и магнитного диполей и всего элемента в плоскости уОх (рисунок 7.1, в) соответственно выражаются уравнениями:

F'(θ_а)=1, F" (θ_а)=sinθ_a,

f₂(θ_а)= F'(θ_а)+ F" (θ_а)=1+sinθ_a. (7.2)

Заметим, что угол θ_b отсчитывается от оси диполя в плоскости Е, а угол θ_а – от оси диполя, но в плоскости Н.

Как видно из функций (7.1), (7.2) и ДН (рисунок 7.1, б, в), элемент Гюйгенса – источник однонаправ­ленного излучения: по оси х, где θ_а = π/2 и θ_b = π/2, направлен макси­мум функций направленности, равный f_lm (θ_b) = 2, f_2m (θ_а) = 2, а в противоположном направлении излучения нет. В соответствии со значениями

f_lm (θ_b) = f_2m (θ_а) =2 нормированные функции направ­ленности имеют вид

кардиоиды

F₁(θ_b)=(1+ sin θ_b) /2, (7.3)

F₂(θ_a)=(1+ sin θ_a) /2. (7.4)

Пря­моугольный волновод, возбуждаемый на волне Н₁₀, имеет в плоскости Е (по размеру b) равномерное и синфазное поле.

В плоскости Н (по размеру а) того же волновода поле неравномерное и амплитуда электрического поля изменяется по косинусоидальному закону Е_т =Е_тт cos (πy/а) (координатные оси расположены так, как на рисунке 7.2).

Однако, предположим, что поле в плоскости Н тоже является равномерным и синфазным.

Тогда на плоском прямо­угольном раскрыве со сторонами а, b имеется большое число n элементов Гюйгенса (n=(a/dу)(b/dz)),и этот раскрыв по всей по­верхности синфазно и равномерно возбуждается элементами Гюйгенса. Каждый горизонтальный ряд таких элементов имеет высоту dz и является непрерывной линейной системой излучателей длиной l_А=а с коэф­фициентом замедления k₃ = 0, а каждый вертикальный ряд элементов Гюйгенса ши­риной dy также является непрерывной линейной системой излучателей длиной l_B=b с коэф­фициентом замедления k₃=0.

Это позволяет представить нормиро­ванные функции направленности системы F(θa) в H-плоскости (уОх ) и F(θ_b) в Е-плоскости (zОх) как произведение одноименных функций направленноcти эле­мента Гюйгенса и множителя системы[2].

, (7.5)

. (7.6)

На рисунке 7.2 показана ДН прямоугольного раскрыва в одной из его главных плоскостей (а) и ее составляющие ДН (б, в)

В поло­жительном направлении оси х (θ_а = θ_b = π/2) обе функции максимальны, а в обратном направлении (θ_a=θ_b = 270°) они за счет множителей 1+ sin θ_b(а) равны нулю.

Следовательно, синфазное воз­буждение плоского раскрыв антенны, как и линейной антенны создает режим поперечного излучения с главным максимумом,

направлен­ным по оси х (рисунок 7.3).

Рисунок 7.2 – ДН прямоугольного раскрыва в одной из его главных

плоскостей (а) и ее составляющие ДН (б, в)

Рисунок 7.3 - Пространственная ДН прямоугольного раскрыва

Ширина главного лепестка ДН на нулевом уровне и на уровне половинной мощности определяется из выражений [5]

(7.7)

(7.8)

Отсюда, чем больше вертикальный (горизонтальный) размер раскры­ва, по сравнению с длиной волны, тем уже главный лепесток ДН этого раскрыва в вертикальной (горизонтальной) плоскости и больше число боковых лепестков ДН.

С учетом неравномерности электрического поля волновода в плоскости Н (по размеру а) нормированная функция направленности для плоскости Н принимает вид[5]

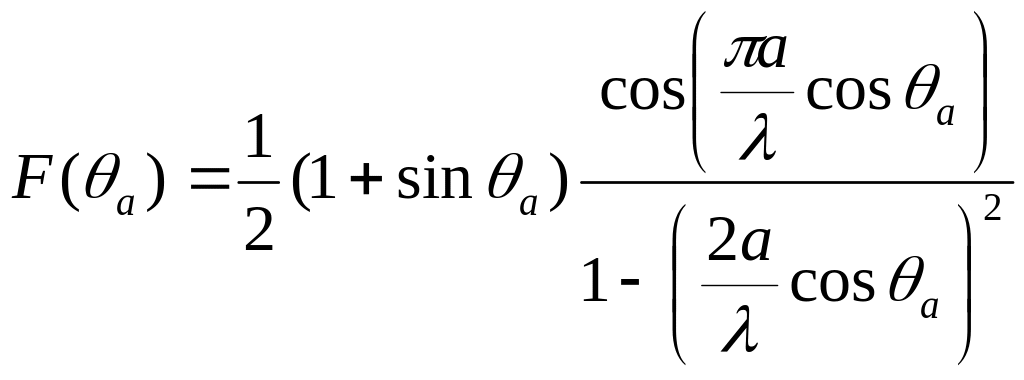. (7.9)

Построенная по этому уравнению ДН имеет более широкий главный лепесток (2 θ_0,5⁰ = 68λ/а), но более низкие уровни боковых лепест­ков, чем имела бы ДН при одинаковой амплитуде поля по плоскости Н раскрыва. Такой результат объясняется тем, что ослабление поля к краям раскрыва эквивалентно уменьшению размера а.

Если бы во всем отверстии соблюдалась равномерность фазы и амплитуды, то его эффективная S_эф и геометрическая S_A поверхности были бы равны между собой. В данном случае за счет косинусоидального распределения поля в плоскости Н коэффициент использования площади излучателя снижается от v = 1 до v= 0,81 и S_эф= vS_A =0,81ab. Принимая а=0,71λ , b =0,35 λ , находим коэффициент на­правленного действия волноводного излучателя

.

Действительные условия излучения несколько отличаются от опи­санных, так как поле в отверстии волновода не совпадает полностью с полем в поперечном сечении волновода. Причины несовпадения сле­дующие. Во-первых, из-за неравенства волновых сопротивлений вол­новода и свободного пространства имеет место частичное отражение энергии от раскрыва (k_бв= 0,6 ... 0,7) и во-вторых, в связи с отсутствием ограничений для возбуждения волн высших типов последние возникают у открытого конца волновода, а это порождает боковые лепе­стки в ДН.

Открытый конец волновода, как видно, является неэффективным излучателем вследствие малых размеров отверстия (эти размеры обыч­но меньше длины волны) и значительных отражений при переходе волны в открытое пространство.