Литература.

1. Р.И. Грабовский Курс физики. – СПб.: Лань, 2012. – 607с.

2. А.Н. Ремизов, А.Я. Потапенко Курс физики. – М.: Дрофа, 2006. – 720 с.

3. Савельев И.В. Курс общей физики. М., 1977- 1979, т 1, 2.

4. А.Г. Чертов, А.А. Воробьев Задачник по физике. – М.: Физматлит, 2003. – 637 с

5. Сборник задач по физике /Под ред. Р.И. Грабовского. – СПб.: Лань, 2012. – 127 с.

Учебные материалы по разделам курса физики.

Раздел 1. Физические основы механики Основные формулы.

1.Поступательное движение

1. Кинематическое уравнение движения материальной точки (центра масс тела) вдоль оси х: x=f(t),

где f(t)–некоторая функция от времени.

2. Средняя скорость : <V_x>=

3. Средняя путевая скорость : <V>=

где s- путь, пройденный точкой за интервал t. Путь s в отличии от разности координат (х=х₂-х₁) не может убывать и принимать отрицательные значения, т.е. s 0. Поэтому <V>  |<V_x>|.

4. Мгновенная скорость: V_x= .

5. Среднее ускорение: <а_x>=

6. Мгновенное ускорение: а_x= .

2. Вращательное движение.

7.Кинематическое уравнение движения материальной точки по окружности: =f(t); r=R=const.

8.Угловая скорость: =

9.Угловое ускорение: =

10.Связь между линейными и угловыми величинами, характеризующими движение точки по окружности:

v=R; a_=R; a_n=²R,

где v– линейная скорость, a_ и a_n - тангенциальное и нормальное ускорения;  - угловая скорость; - угловое ускорение; R-радиус окружности.

11.Полное ускорение:

12.Угол между полным ускорением и нормальным : =arccos( )

3.Колебательное движение и волны.

13.Кинематическое уравнение гармонических колебаний материальной точки: x=Acos(t+),

где х- смещение; А- амплитуда колебаний; - круговая или циклическая частота; - начальная фаза.

14.Скорость материальной точки, совершающей гармонические колебания: v=-Asin(t+),

15.Ускорение материальной точки, совершающей гармонические колебания: a=-A²cos(t+),

16.Сложение гармонических колебаний одного направления и одинаковой частоты:

а) амплитуда результирующего колебания:

б) начальная фаза результирующего колебания:

17.Траектория точки, учавствующей в двух взаимно- перпендикулярных колебаниях: (x=A₁cost, y=A₂cos(t+)):

1. (если разность фаз =0);

2. (если разность фаз =);

3. (если разность фаз = );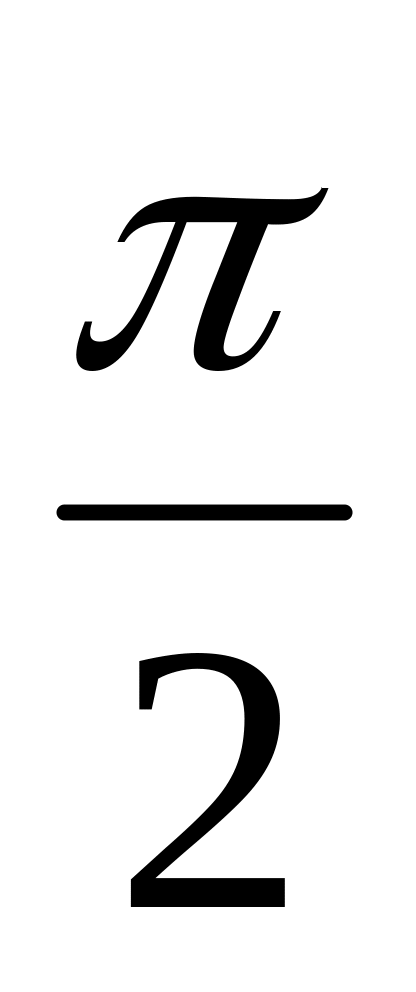

18.Уравнение плоской бегущей волны: у=Acos(t- ),

где у- смещение любой из точек среды с координатой х в момент t; v- скорость распространения колебаний в среде.

19.Связь разности фаз  колебаний с расстоянием х между точками среды, отсчитанным в направлении распространения колебаний: = ,где - длина волны.

Динамика.

1.Поступательное движение.

20.Импульс материальной точки массой m, движущейся поступательно со скоростью v:

.

21.Второй закон Ньютона: ,

где – сила, действующая на тело.

22.Силы, рассматриваемые в механике:

а) сила упругости: F=-kx,

где k- коэффициент упругости (в случае пружины- жесткость); х- абсолютная деформация;

б) сила тяжести: G=mg;

в) сила гравитационного взаимодействия:

где - гравитационная постоянная; т₁ и т₂ – массы взаимодействующих тел; r-расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряженность G гравитационного поля:

F=mG;

г) сила трения (скольжения): F=fN,

где f- коэффициент трения; N – сила нормального давления.

23.Закон сохранения импульса:

или для двух тел (i=2): m₁v₁+ m₂v₂= m₁u₁+ m₂u₂,

где v₁ и v₂ –скорости тел в момент времени, принятый за начальный; u₁ и u₂- скорости тех же тел в момент времени, принятый за конечный.

24.Кинетическая энергия тела, движущегося поступательно: или

25.Потенциальная энергия:

а) упругодеформированной пружины: ,

где k- жесткость пружины, х- абсолютная деформация.

б) гравитационного взаимодействия:

где - гравитационная постоянная; т₁ и т₂ – массы взаимодействующих тел; r-расстояние между телами (тела рассматриваются как материальные точки).

в) тела, находящегося в однородном поле силы тяжести: П=mgh,

где g- ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<R, где R- радиус Земли).

26. Закон сохранения механической энергии: E=Т+П=const.

27. Работа А, совершаемая внешними силами, определяется как мера изменения энергии системы: А=Е=Е₂-Е₁.