Вопрос 28

Расчет э.д.у. между параллельными бесконечно тонкими проводниками неограниченной длины

Силы взаимодействия прямолинейных, произвольно направленных проводников с исчезающее малым сечением могут быть определены из выражения Лапласа – Био и Савара, согласно которому на каждый элемент dl₂проводника 2 с током I₂, находящегося в магнитном поле проводника 1 с током I₁, действует сила

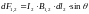
Где B_1,2– индукция (в месте расположения элемента dl₂) магнитного поля соседнего проводника с током I₁; θ - угол, определяемый направлениями вектор B_1,2и вектор dl₂

Индукция B_1,2 по длине проводника 2 может быть определена интегрированием в соответствующих пределах выражения

В котором µ = 4π·10^-7 – магнитная проницаемость воздуха, Гн/м; r_1,2– радиус, проведенный от элемента dl₁ в точку наблюдения на проводнике 2 ;α – угол, определяемый направлениями вектора dl₁ и вектора r_1,2.

Взаимодействие тонких параллельных проводников.

Если длина проводников не ограничена, магнитное поле плоскопараллельно. Магнитная индукция в любой точке проводника 2 может быть определена:

Индукция постоянна вдоль проводника и обратно пропорциональна расстоянию а. Следовательно, электродинамическая сила, отнесенная к единице длины проводника, также постоянна по длине. Она может быть определена из выражения:

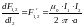
Сила на длине l равна:

Направление электродинамических сил зависит от направления токов и может быть определено по правилу левой руки. При одинаковом направлении токов проводники притягиваются, при противоположном – отталкиваются.

Вопрос 29

Влияние формы и размеров поперечных сечений проводников на величину э.д.у.

При определении электродинамических усилий по формуле

исходят из условия, что ток протекает по оси круглых проводников, диаметр которых не оказывает влияния на величину усилий. Следует заметить, что размеры и форма сечения проводников при больших расстояниях между ними не оказывают сколько-нибудь заметного влияния на величину электродинамических усилий.

Если же проводники имеют форму прямоугольных полос и расположены на небольшом расстоянии друг от друга, когда расстояние в свету меньше периметра полосы, то размеры их сечения могут оказать существенное влияние на электродинамические усилия. Это влияние поперечных размеров проводника при расчетах учитывается при помощи коэффициента формы.

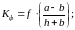
а,b, h – геометрические параметры проводника

Вопрос 30

Электродинамические усилия при трехфазном токе

Рассмотрим электродинамическое взаимодействие между тремя лежащими в одной плоскости параллельными проводами или шинами А, В, С по которым протекает трёхфазный ток.

Мгновенные значения токов в фазах А, В, С:

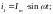
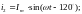
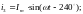
При трёхфазном токе происходит взаимодействие между шинами, в которых токи сдвинуты по фазе на 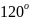, и на каждый проводник одной фазы действуют усилия со стороны проводников двух других фаз.

Очевидно, что при расположении фаз в одной плоскости шины крайних и средней фаз находятся в различных условиях, так как взаимодействующие проводники с током удалены в первом случае на разные расстояния а и 2а, а в другом случае на равные расстояния а. Электродинамические усилия создают нагрузку, равномерно распределённую по длине провода или шины.

На шину фазы А действуют электродинамические усилия, создаваемые токами, протекающими в шинах В и С.Усиление, действующее на шину фазы А, складывается из усилия между шинами фаз А и В и между шинами А и С.

Силы взаимодействия между шинами фаз А и В (при равных токах фаз) и между шинами той же фазы А и фазы С:

Следовательно, на шину А будет действовать усилие, равное алгебраической сумме силf_AB и f_AC и при ωt=75⁰(для первого периода)будет иметь максимальное значение:

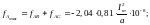
Знак минус указывает, что результирующее максимальное усиление по отношению к соседним фазам будет отталкивающим.

Для шины фазы С подобным путём можно получить

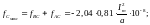
Таким же способом найдём максимальное усилие, действующее на шину средней фазы В.Одно из направлений действия сил от фазы В к А примем за положительное, тогда:

Максимум отталкивающего усилия от фазы А при ωt=75⁰(для первого периода) и максимум притягивающего усилия к той же фазе при ωt=165⁰. При этих значениях ωtмаксимальное усилие, действующее на среднюю фазу В, будет:

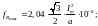
Отсюда следует, что эти усилия не постоянны, они изменяются по величине и направлению и пульсируют с двойной частотой переменного тока. Максимальные и минимальные значения усилий для фаз (проводов, шин) А и С одинаковы, но максимумы и минимумы наступают не одновременно.

Максимальное усилие, действующее на среднюю фазу В(шин), на 7% больше, чем на крайние А и С:

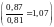
Исходя из этого вывода, средняя фаза должна являться расчётной при проверке на динамическую механическую прочность шинных конструкций и аппаратов трёхфазных систем.

Для обеспечения надлежащей механической прочности шин, проводников и аппаратов требует расчёты на электродинамическую прочность производить по наибольшим возможным электродинамическим усилиям, которые могут возникнуть в данной конструкции.Такие усилия получаются при ударном токе КЗ:

а затем они уменьшатся по мере затухания тока КЗ.

Соответствующее этому условию выражение для наибольшего усилия на среднюю фазу с учётом апериодической составляющей тока трёхфазного КЗ будет

где i_у- ударный ток трёхфазного короткого замыкания, кА; а – расстояние между осями шин смежных фаз, см.

Если провода или шины расположены по вершинам равностороннего треугольника, то максимальное усилие на каждый провод равно максимальному усилию, действующему на средний провод при их расположении в одной плоскости.

Величина наибольшего усилия, которое приходится на опорный изолятор сборных шин, будет

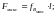
гдеf_Bмакс - максимальное усилие на единицу длины шины средней фазы, кГ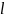/см; – длина пролёта шин – расстояние между опорными изоляторами, см.