Федеральное государственное образовательное бюджетное учреждение

высшего профессионального образования

«Финансовый университет при Правительстве Российской Федерации»

(Финуниверситет)

Смоленский филиал Финуниверситета

Кафедра Математики и информатики

КОНТРОЛЬНАЯ РАБОТА №1

по дисциплине «Эконометрика»

Вариант: 10

Студент: Яренкова Валерия Алексеевна

Факультет: Бух. учёт АиА

Направление: экономика

Группа: СМЛС14-1Б-ЭК03

№ зачетной книжки: 100.25/1403030

Руководитель: Гусарова Ольга Михайловна

Смоленск 2016

Вопрос: Понятие статистической гипотезы. Процедура проверки статистической гипотезы

Статистическая гипотеза – любое предположение, касающееся неизвестного распределения случайных величин (элементов), соответствующее некоторым представлениям об изучаемом явлении. В частном случае это может быть утверждение о значениях параметров распределения генеральной совокупности.

Различают нулевую и альтернативную гипотезы. Нулевая гипотеза – гипотеза, подлежащая проверке. Альтернативная гипотеза – каждая допустимая гипотеза, отличная от нулевой. Нулевую гипотезу обозначают Н₀, альтернативную – Н₁ (от Hypothesis – «гипотеза» (англ.)).

Конкретная задача проверки статистической гипотезы полностью описана, если заданы нулевая и альтернативная гипотезы. При обработке реальных данных большое значение имеет правильный выбор гипотез. Принимаемые предположения, например, нормальность распределения, должны быть тщательно обоснованы, в частности, статистическими методами. Необходимо помнить, что в подавляющем большинстве конкретных прикладных задач распределение результатов наблюдений в той или иной степени отлично от нормального.

Процедура проверки гипотез обычно проводится по следующей схеме:

1. Формулируются гипотезы Н0 и Н1.

2. Выбирается уровень значимости критерия.

3. По выборочным данным вычисляется значение некоторой случайной величины, называемой статистикой критерия, или просто статистическим критерием, который имеет известное стандартное распределение (нормальное, Т-распределение Стьюдента и т.п.)

4. Вычисляется критическая область и область принятия гипотезы. То есть находят критическое (граничное) значение критерия при выбранном уровне значимости.

5. Найденное значение критерия сравнивается с критическим и по результатам сравнения делается вывод: отвергнуть гипотезу или не отвергнуть. Если вычисленное по выборке значение критерия меньше чем критическое, то нулевую гипотезу Но не отвергают на заданном уровне значимости.

В этом случае наблюдаемое по экспериментальным данным различие генеральных совокупностей можно объяснить только случайностью выборки. Однако это совсем не означает доказательства равенства параметров генеральных совокупностей. Просто имеющийся в распоряжении статистический материал не дает оснований для отклонения гипотезы о том, что эти параметры одинаковы. Возможно, появится другой экспериментальный материал, на основании которого эта гипотеза будет отклонена.

Если вычисленное значение критерия больше критического, то гипотеза Н0 отклоняется в пользу гипотезы Н1 при данном уровне значимости.

В этом случае наблюдаемое различие генеральных совокупностей уже нельзя объяснить только случайностями и говорят, что наблюдаемое различие значимо (статистически значимо) на выбранном уровне значимости.

Следует подчеркнуть разницу между статистической значимостью и практической значимостью. Заключение о практической значимости всегда делается человеком, изучающим данное явление. И здесь истинным критерием является опыт и интуиция исследователя, а статистические критерии значимости — лишь формально точный инструмент, используемый в исследовании. Чем больше исследователь знает об изучаемом явлении, тем точнее будет сформулированная им гипотеза и тем точнее будут выводы, сделанные с помощью критериев значимости.

В настоящее время при проверке гипотез, особенно с использованием специализированных программных средств, уровень значимости до эксперимента точно не устанавливается, а по экспериментальным данным вычисляется вероятность Р того, что критерий (статистика критерия) выйдет за пределы значения, рассчитанного по выборке. Таким образом, Р — это экспериментальный (эмпирический уровень значимости. Точное значение Р обычно не указывают, а окончательные результаты приводят, сравнивая вычисленное значение критерия со стандартными значениями. Если, например, Р не превосходит 0,05, то на уровне значимости 5% различие считается статистически незначимым.

Критерии значимости подразделяются на три типа:

1. Критерии значимости, которые служат для проверки гипотез о параметрах распределений генеральной совокупности (чаще всего нормального распределения). Эти критерии называются параметрическими.

2. Критерии, которые для проверки гипотез не используют предположений о распределении генеральной совокупности. Эти критерии не требуют знания параметров распределений, поэтому называются непараметрическими.

3. Особую группу критериев составляют критерии согласия, служащие для проверки гипотез о согласии распределения генеральной совокупности, из которой получена выборка, с ранее принятой теоретической моделью (чаще всего нормальным распределением).

• Задача 1. Построение модели парной регрессии

1. Рассчитайте матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов корреляции.

2. Постройте поле корреляции результативного признака и наиболее тесно связанного с ним фактора.

3.  Рассчитайте параметры линейной парной регрессии от ведущего фактора.

4.  Оцените качество уравнения парной регрессии через коэффициент детерминации, среднюю ошибку аппроксимации и F-критерий Фишера.

5. Осуществите прогнозирование среднего значения показателя при уровне значимости 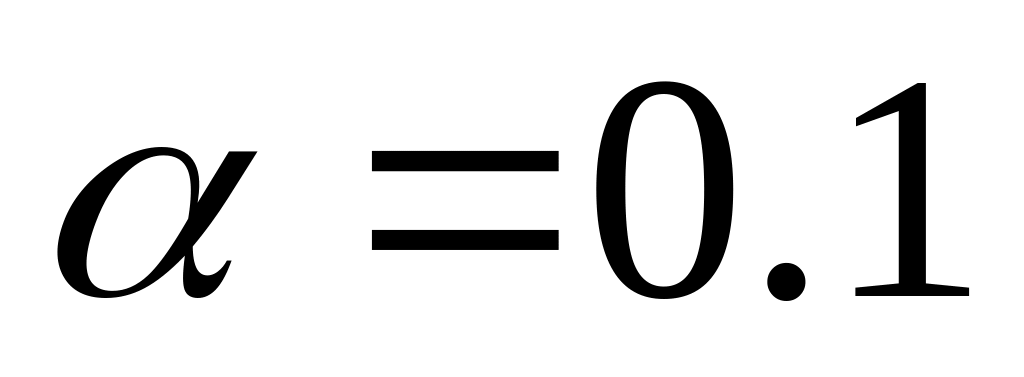, если прогнозное значения фактора составит 80% от его максимального значения. Представьте графически: фактические и модельные значения, точки прогноза.

По тринадцати коммерческим банкам имеются данные, характеризующие зависимость годовой прибыли от размера собственного капитала, общей суммы привлеченных средств и среднегодовых ставок по рублевым депозитам и краткосрочным кредитам:

№ банка	Прибыль (млн. руб.)	Собственный капитал (млн. руб.)	Привлеченные средства (млн. руб.)	Депозитная ставка (% годовых)	Кредитная ставка (% годовых)
1	115	4428	3278	12,5	17,7
2	80	3756	5696	11,7	18,2
3	97	2970	2210	11,2	19,1
4	92	6231	5823	9,7	15,2
5	129	3960	4569	13,5	18,5
6	223	7354	2896	10,8	18,6
7	251	4662	3526	12,1	15,7
8	267	4760	2259	11,7	16,6
9	137	4569	4596	13,7	17,3
10	163	5274	3271	12,5	19,3
11	225	5418	4596	12,8	17,8
12	278	5359	3256	11,2	14,5
13	367	8254	5189	10,4	13,7

1) построили в excel матрицу парных корреляций

Вводим исходные данные

Для построения матрицы парных коэффициентов корреляции воспользуемся инструментом Корреляции. Данные-Анализ данных-корреляция.

Заполняем необходимые поля диалогового меню

Для анализа матрицы парных корреляций нужно выполнить следующее:

1. Выберем главный ведущий фактор.

В нашей матрице наибольшее значение 0,6465

1.2. установим фактор наличия мультиколлинеарности.

В данной области отсутствуют коэффициенты большие по модулю 0.8, следовательно, в матрице отсутствуем мультиколлинеарность, следовательно, все эти факторы можно внести в модель регрессии.

2. Построим поля корреляции результативного признака (Y) и наиболее тесно связанного с ним фактора (х1)

3. Строим модель парной регрессии. Для этого воспользуемся инструментом Регрессия Данные-анализ данных-регрессия

Выбираем данные.

Результат построения регрессии

Параметрами регрессии являются значения в 3 таблице, коэффициенты.

Y= – 17,3204

X1= 0,0395

На основании полученных данных можно записать уравнение парной регрессии

Y= – 17,3204 + 0,0395*x1

4. Коэффициент детерминации, среднюю ошибку аппроксимации мы получили в результате расчётов, приведенных в пункте 3.

Коэффициент детерминации определяет какая доля вариации признака (Y) учтена в модели и обусловлена влиянием на него фактора (X1). Чем больше значение коэффициента детерминации, тем теснее связь между признаками в построенной математической модели

R² =0,418 следовательно качество построенного уравнения регрессии – удовлетворительное.

F-расчетное =7,897, а F-табличное F= 4,84 это значит, что уравнение регрессии является статистически значимым. Такое уравнение целесообразно использовать для анализа и прогнозирования.

Среднюю ошибку аппроксимации рассчитаем по формуле:

Среднее значение прибыли рассчитаем в Excelс помощью функции СРЗНАЧ.

= 186,4615385

А  0,34 %

В формульном выражении: