10) Другая запись формулы Тейлора и остаточного члена.

Часто формулу Тейлора 1 записывают в ином виде, положим в (1) а=х₀

х-а=∆х;

х=х₀+∆х, тогда *(∆х)n-1; (5)

0<θ<1

При n=0 из (5) получается формула Лагранжа.

Покажем, что если функция f⁽ⁿ⁺¹⁾ ограничена в окрестности точки (а), то остаточный член

R_n+1(x) является бесконечно малой более высокого порядка, чем(х-а)ⁿ, x→a.

lim_{x→a ;}

Таким образом R_n+1(x)=0[(x-a)ⁿ] при x→а (6)

формула (6) называется остаточным членом в форме Пеано.

11) Формула Маклорена.

Формулой Маклорена называют формулу Тейлора (1), при а=0

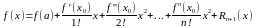; Остаточный член имеет вид:

1. В форме Логранжа.

2. В форме Пиано.

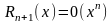
С помощью формулы Маклорена функцию можно с определённой степенью точности заменять многочленами, являющимися наиболее простыми элементарными функциями.

28) Интерполяционная формула Лагранжа.

Рассмотрим вопрос об отыскании коэффициентов интерполяционного многочлена. Представим многочлен в системе уравнений: a0+a1x0+…+anx0n=y0 …a0+a1xn+…+anxnn=yn. Найдя коэффициенты а получаем саму интерполяционную формулу : Pn=((x-x1)…(x-xn)/(x0-x1)…(x0-xn))y0+…+((x-x0)…(x-xn-1)/(xn-x0)…(xn-xn-1))yn

33) Ряды (основные понятия). Сходимость ряда.

Числовым рядом называется бесконечная последовательность чисел u₁,u₂,…,u_n соединённые знаком сложения. u₁,u₂,…,u_n – члены ряда. u_n – общий член или n-ый член ряда. Заданный – ряд в котором известен u_n. Обратная задача – по нескольким первым членам написать общий член – имеет бесконечное множество решений.

Ряд называется сходящимся если существует конечный придел последовательности его частных сумм. lim при (n→∞)S_n=S. S – сумма ряда. В этом случае можно записать u₁+u₂+…+u_n=S. Если конечного предела последовательности конечных сумм не существует, то ряд называется расходящимся.

34) Необходимый признак сходимости. Гармонический ряд.

Теорема (Необходимый признак сходимости). Если ряд сходится то придел общего члена u_n при n→∞ равен 0.

Следствие. Если предел общего члена u_n при n→∞ <>0, то ряд расходится.

Замечание. Рассмотренная теорема выражает лишь необходимый, но не достаточный признак сходимости ряда. Если lim при (n→∞)u_n=0, то из этого не следует что ряд сходится.

35) Ряды с положительными членами.

Теорема (Признак сравнения). Пусть даны два ряда с положительными членами u₁+u₂+…+u_n и v₁+v₂+…+v_n, причём члены первого ряда не превосходят члены второго, т.е. при любом n u_n<b_n. Тогда: a) если расходится u₁+u₂+…+u_n, то расходится v₁+v₂+…+v_n;

b) если сходится u₁+u₂+…+u_n, то сходится v₁+v₂+…+v_n.

Теорема (Предельный признак сравнения). Если u₁+u₂+…+u_n и v₁+v₂+…+v_n ряды с положительными членами и существует конечный предел отношения их общих членов lim при (n→∞)u_n/v_n=k<>0, то ряды одновременно сходятся, либо расходятся.

Теорема (Признак Даламбера). Пусть для ряда u₁+u₂+…+u_n с положительными членами существует предел отношения (n+1) члена к n–ому члену. lim при (n→∞)u_n+1/v_n=l, тогда если l<1, то ряд сходится, а если l>1, то ряд расходится, если l=1, то вопрос о сходимости ряда остаётся не решенным.

Замечание. lim при (n→∞)u_n+1/v_n=∞, то ряд расходится.

Теорема (Интегральный признак сходимости). Пусть дан ряд u₁,u₂,…,u_n члены которого положительны и не возрастают, а функция f(x) определена при х=>1. Непрерывна и не возрастающая тогда для сходимости ряда u₁+u₂+…+u_n необходимо и достаточно чтобы сходился несобственный интеграл lim при (R→∞)∫₁^∞f(x)dx.