19. Ошибка репрезентативности средних величин, методика расчета, значение.
В статистике выделяют два основных метода исследования - сплошной и выборочный. При проведении выборочного исследования обязательным является соблюдение следующих требований: репрезентативность выборочной совокупности и достаточное число единиц наблюдений. При выборе единиц наблюдения возможны ошибки смещения, т.е. такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объективными и закономерными. При определении степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки - случайная ошибка репрезентативности (m) - является фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования и аналогичными величинами, которые были бы получены при проведении исследования на генеральной совокупности.
Оценка достоверности результатов исследования предусматривает определение:
1. ошибки репрезентативности
2. доверительных границ средних (или относительных) величин в генеральной совокупности
3. достоверности разности средних (или относительных) величин (по критерию t)
Расчет ошибки репрезентативности (mм) средней арифметической величины (М):
,
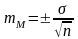где σ
- среднее квадратическое отклонение; n
- численность выборки (>30).
В клинических и экспериментальных работах довольно часто приходится использовать малую выборку, когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, число наблюдений уменьшается на единицу, т.е.
;
.
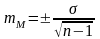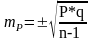Величина ошибки репрезентативности зависит от объема выборки: чем больше число наблюдений, тем меньше ошибка. Для оценки достоверности выборочного показателя принят следующий подход: показатель (или средняя величина) должен в 3 раза превышать свою ошибку, в этом случае он считается достоверным.
20. Ошибка репрезентативности относительных величин, методика расчета,
значение. В статистике выделяют два основных метода исследования - сплошной и выборочный. При проведении выборочного исследования обязательным является соблюдение следующих требований: репрезентативность выборочной совокупности и достаточное число единиц наблюдений. При выборе единиц наблюдения возможны ошибки смещения, т.е. такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объективными и закономерными. При определении степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки - случайная ошибка репрезентативности (m) - является фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования и аналогичными величинами, которые были бы получены при проведении исследования на генеральной совокупности.
Оценка достоверности результатов исследования предусматривает определение:
1. Ошибки репрезентативности
2. Доверительных границ средних (или относительных) величин в генеральной совокупности
3. Достоверности разности средних (или относительных) величин (по критерию t)
Расчет ошибки репрезентативности (mР) относительной величины (Р):
,
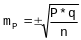где Р - соответствующая относительная
величина (рассчитанная, например, в %);
q =100 - Ρ% - величина, обратная Р; n - численность выборки (n>30)
В клинических и экспериментальных работах довольно часто приходится использовать малую выборку, когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, число наблюдений уменьшается на единицу, т.е.
; .
Величина ошибки репрезентативности зависит от объема выборки: чем больше число наблюдений, тем меньше ошибка. Для оценки достоверности выборочного показателя принят следующий подход: показатель (или средняя величина) должен в 3 раза превышать свою ошибку, в этом случае он считается достоверным. 19 и 20 вопрос практически одинаковые, В скобках про относ. Величину написано