
- •Квантовая яма, квантовый барьер. Уровни размерного квантования.
- •Резонансное туннелирование. Резонансно-туннельный диод.
- •Псевдоморфные и метаморфные гетероструктуры. Правило Вегарда.
- •Классический эффект Холла в двумерном газе электронов.
- •Целочисленный квантовый эффект Холла и стандарт сопротивления. Роль примесного рассеяния.
- •Одноэлектроника. Кулоновская блокада туннелирования(вах).
- •Мемристор.
- •Графен, нанотрубки, фуллерены (основные типы).
- •Сверхпроводники: эффект Мейсснера, квантование потока.
ПОЧИТАТЬ, НО НЕ ОБЯЗАТЕЛЬНО
ДОПОЛНЕНИЕ ИЗ ЛЕКЦИЙ
ХЗ ЧТО ЭТО И НАДО ЛИ
ВРОДЕ НАДО А ВРОДЕ И НЕТ
1
Зонная структура основных полупроводников.

2
Гетеропереход. Зонная диаграмма. Основные типы гетероструктур.

Основным элементом гетероструктур различного типа является гетеропереход. Под гетеропереходом понимается контакт двух различных по химическому составу полупроводников, при котором кристаллическая решетка одного материала без нарушения периодичности переходит в решетку другого материала. Различают изотипные и анизотипные гетеропереходы.
Если гетеропереход образован двумя полупроводниками одного типа проводимости, то говорят об изотипном гетеропереходе. Анизотипные гетеропереходы образуются полупроводниками с разным типом проводимости. Существует три модели гетероперехода:
I -идеальный гетеропереход;
II -неидеальный гетеропереход;
III -гетеропереход с промежуточным слоем.
Гетеропереходы разделяются на следующие три типа:
• I
тип: запрещенная зона
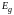 одного из композиционных материалов
лежит внутри запрещенной зоны другого
материала (
одного из композиционных материалов
лежит внутри запрещенной зоны другого
материала ( ).
При условии
).
При условии
 высота потенциального барьера на
интерфейсе A/B составляет
высота потенциального барьера на
интерфейсе A/B составляет
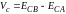 для электронов и
для электронов и
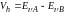 для дырок, где
для дырок, где
 - энергетическое положение дна зоны
проводимости
- энергетическое положение дна зоны
проводимости
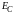 и потолка валентной зоны
и потолка валентной зоны
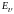 в материале
в материале
 .
.
• II тип:
a:
для гетероперехода A/B
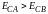 ,
,
 .
Для указанных пар
.
Для указанных пар
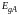 и
и
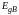 перекрываются (
перекрываются (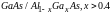 ,
,
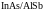 ,
,
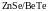 ).
).
b:
запрещенные зоны не перекрываются и
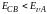 .
.
• III
тип: один из слоёв гетероперехода A/B
является бесщелевым(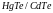 ),
то есть
),
то есть
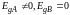
В идеальном гетеропереходе, в отличие от неидеального, на границе раздела материалов отсутствуют локальные энергетические состояния для электронов. Гетеропереход с промежуточным слоем формируется через слой конечной толщины, и локальные энергетические состояния могут существовать как в самом промежуточном слое, так и на границах его раздела.

Для построения энергетической диаграммы часто применяют простое «правило электронного сродства» (в англоязычной литературе – правило Андерсона), согласно которому разрыв зоны проводимости равен разности электронного сродства двух материалов. Но следует иметь в виду, что данный подход далеко не всегда справедлив, так как в разрыв зон зависят еще и от деталей формирования связей на гетерогранице и деформационного потенциала. Для построения энергетической диаграммы идеального гетероперехода должны быть известны следующие характеристики полупроводников:
-ширина запрещенной зоны (Eg1, Eg2). При построении считаем, что Eg2>Eg1;
-термодинамическая работа выхода (Ф1, Ф2) – расстояние от уровня Ферми(от уровня легирования материала) полупроводника до уровня вакуума.
-сродство к электрону (χ1, χ2) – расстояние от дна зоны проводимости до
уровня вакуума.
Полное изменение потенциальной энергии равно разности работ выхода, что обеспечивает неизменное положение уровня Ферми вдоль гетероперехода. До «приведения в контакт» двух полупроводников потенциальная энергия электронов в них разная из-за разной термодинамической работы выхода. При «соприкосновении» двух полупроводников, как и в случае обычного p-n-перехода, электроны начнут «переходить» из полупроводника с меньшей работой выхода в полупроводник с большей. Это будет происходить до тех пор, пока диффузионный ток не будет скомпенсирован дрейфовым током носителей заряда под воздействием поля, созданным избыточными
носителями. При этом возникнет контактная разность потенциалов
ϕ0 = Ф2 −Ф1 (1)
и образуется область пространственного заряда шириной d (Рисунок 1). При таком построении видно, что из-за различия электронного сродства в контактирующих полупроводниках дно зоны проводимости первого
полупроводника выходит на плоскость контакта в точке, не совпадающей в общем случае с точкой выхода на эту плоскость дна зоны проводимости второго полупроводника – формируется разрыв зоны проводимости ∆Ec. Он равен:
∆Ec = χ1 − χ 2 (2)
Аналогично формируется и разрыв валентной зоны. Он равен:
∆Ev = Eg − Eg − ∆Ec 2 (3)
Следует заметить, что разрывы зон могут быть как положительными так и отрицательными.

Роль кулоновского взаимодействия.
Механизм сужения заключается в кулоновском взаимодействии неосновного носителя с газом основных носителей. Кулоновское притяжение будет уменьшать энергию активации образования электронно-дырочной пары или, иными словами, запрещенную зону полупроводника, на величину:
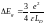
Дебаевская
длина волны 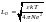 - для невырожденного газа.
- для невырожденного газа.
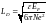 -
для вырожденного газа.
-
для вырожденного газа.
3
Квантовая яма, квантовый барьер. Уровни размерного квантования.
Квантовые ямы. Этим термином обозначаются системы, в которых имеется размерное квантование движения носителей заряда в одном направлении (квантовая структура, в которой движение электрона ограничено в одном направлении).
Квантовая яма - это мезоскопический объект , характеризующийся потенциальной ямой для подвижных носителей заряда – электронов и дырок, которая ограничивает подвижность частиц с трех до двух измерений, тем самым заставляя их двигаться в плоском слое. Квантово-размерные эффекты проявляют себя когда длина ямы становится сравнима с длиной волны де Бройля частиц (обычно электронов или дырок), и приводят к появлению энергетических минизон.
Энергию
дна каждой из минизон можно приблизительно
оценить с помощью выражения:
 , где
, где
 - номер минизоны,
- номер минизоны,
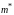 - эффективная масса соответствующей
квазичастицы, - ширина квантовой ямы.
- эффективная масса соответствующей
квазичастицы, - ширина квантовой ямы.

Рисунок
3. Квантовая яма (квантовая плёнка):
дисперсионная зависимость и плотность
состояний

Основные физические явления в квантовых ямах: размерное квантование электронного спектра, квантовый эффект Холла (целочисленный и дробный), при специальном приготовлении очень высокая подвижность электронов. Основные методы получения квантовых ям на гетероструктурах: металлоорганическая газовая эпитаксия и молекулярно-пучковая эпитаксия (эпитаксия — метод выращивания кристаллов на поверхности подложки).
Структуры с туннельно-прозрачными барьерами (системы квантовых ям и сверхрешетки). Основные физические явления в таких системах: резонансное туннелирование; формирование минизонного спектра в сверхрешетках ‑ периодических системах, содержащих много квантовых ям, разделенных туннельно-прозрачными барьерами; нелинейные электрические и оптические явления в сверхрешетках. Методы выращивания этих структур те же, что и для квантовых ям.

Рассмотрим основную идею размерного квантования на примере электронов, находящихся в очень тонкой металлической или полупроводниковой пленке толщиной а. То обстоятельство, что в обычных условиях носители сосредоточены в пленке и не выходят из нее в окружающую среду, означает, что материал пленки (металл или полупроводник) представляет собой потенциальную яму для электронов глубиной, равной работе выхода W, и шириной а. Согласно законам квантовой механики, энергия электронов в такой яме квантуется, т.е. может принимать лишь некоторые дискретные значения Еn , где n имеет целочисленные значения 1,2,3,… . Эти дискретные значения называют уровнями размерного квантования. Типичные значения работы выхода в большинстве твердых тел имеют величину W = 4-5 эВ, на несколько порядков превышающую характерную тепловую энергию носителей kТ, равную при комнатной температуре 0.026 эВ. Поэтому потенциальную яму можно считать бесконечно глубокой (рис.1 а). Если пленка занимает область 0<z<а, то в этом случае энергетические уровни квантовых состояний выглядят следующим образом:
 (1)
(1)
где
m- эффективная масса электрона. Другим
необходимым условием, позволяющим
считать яму бесконечно глубокой, является
малость значений Еn , по сравнению с ее
действительной глубиной W. Это условие,
которое для нижних уровней можно записать
в виде
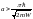 ,
при
,
при
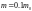 соответствует
толщинам пленки порядка нескольких
межатомных расстояний. Во всех реальных
структурах это условие соблюдается.
соответствует
толщинам пленки порядка нескольких
межатомных расстояний. Во всех реальных
структурах это условие соблюдается.
Для свободной частицы с эффективной массой, движение которой в кристалле в направлении ограничено непроницаемыми барьерами (т.е. барьерами с бесконечной потенциальной энергией), разрешенные значения волновых векторов блоховских волн имеют вид:
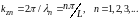 (1)
а
энергия основного состояния по сравнению
с состоянием без ограничения возрастает
на величину
(1)
а
энергия основного состояния по сравнению
с состоянием без ограничения возрастает
на величину
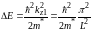 (2)
Это
увеличение энергии называется энергией
размерного квантования частицы.
Энергия размерного квантования является
следствием принципа неопределенности
в квантовой механике. Соответствующее
увеличение кинетической энергии частицы
дается тогда выражением (2). Поэтому
данный эффект часто называют квантовым
размерным эффектом.
(2)
Это
увеличение энергии называется энергией
размерного квантования частицы.
Энергия размерного квантования является
следствием принципа неопределенности
в квантовой механике. Соответствующее
увеличение кинетической энергии частицы
дается тогда выражением (2). Поэтому
данный эффект часто называют квантовым
размерным эффектом.
Кроме
увеличения минимальной энергии частицы
квантовый размерный эффект приводит
также к квантованию энергий ее возбужденных
состояний. Так для бесконечного
одномерного потенциала «прямоугольной
ямы» энергии возбужденных состояний
выражаются как
 где
где
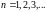 .
.

4
