Примеры постановки задачи оптимизации для решения методами математического программирования

Задача проектирования цилиндрической емкости [6]. Словесная постановка задачи: найти такие значения диаметра и высоты цилиндра, чтобы при фиксированном объеме V общая длина сварных швов была минимальна.

Критерий оптимальности: сварные швы - это две окружности и высота цилиндра, поэтому

Множество допустимых решений задачи: диаметр и высота емкости не могут быть отрицательными числами, т.е. ; объем проектируемой емкости фиксирован и равен , .

Т аким образом, задача состоит в определении таких значений и , что функция достигает минимума и выполняются условия: , d²l/4=V; .

Использование методов оптимизации для анализа и обработки информации. Еще одна область применения оптимизационных методов связана с анализом информации, в частности с проблемой определения параметров некоторой полуэмпирической модели на основе заданного множества экспериментальных данных.

Словесная постановка задачи: предположим, что некоторая переменная зависит от некоторой независимой переменной , а связь между ними задается уравнением

в котором фигурируют два параметра и . Для определения значений и проведена серия экспериментов, в каждом из которых задавалось значение независимой переменной и регистрировалось значение зависимой переменной . Результатом экспериментов является множество пар чисел . Необходимо, на основе полученной информации, подобрать значения и таким образом, чтобы обеспечить наилучшую, в смысле некоторого показателя качества, точность описания экспериментальных данных с помощью функции .

Наиболее часто используемая на практике мера качества экспериментальных данных определяется так называемым критерием наименьших квадратов, в соответствии с которым требуется минимизировать функцию

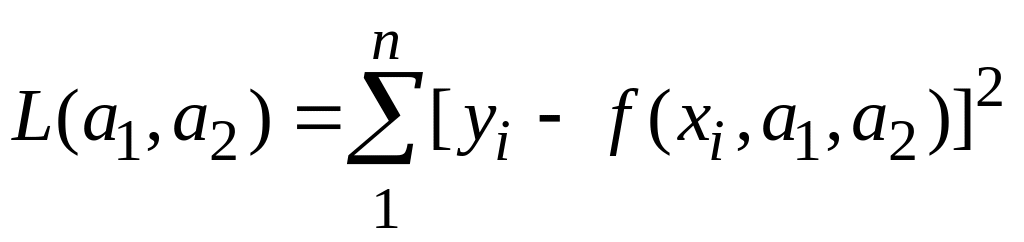Разность показывает, насколько точно выбранная модель соответствует экспериментальным данным и называется остатком. Сумма квадратов по всем экспериментальным данным является мерой точности описания данных. Ясно, что если равно нулю, то сделанный выбор и обеспечивает точное описание. Таким образом, задачу описания данных можно рассматривать как задачу оптимизации, в которой требуется найти значения параметров и , минимизирующие функцию .

Задача планирования выпуска продукции. Словесная постановка задачи: с учетом имеющихся запасов сырья и парка оборудования составить план выпуска продукции, при котором предприятие получит максимальную прибыль.

Пусть цех выпускает четыре вида продукции , запас сырья составляет тонн, в цехе работают человек, для упаковки продукции требуется тара (мешки, бочки), которых в цехе штук. Затраты каждого производственного фактора (сырье, рабочие, тара) на единицу каждого вида продукции составляют , i=1,2,3; j=1,2,3,4 ед./тонну, прибыль с единицы продукта составляет руб/т, j=1,2,3,4. Необходимо определить объемы выпуска продуктов при которых предприятие получит наибольшую прибыль.