
- •Кемерово 2016
- •Тарнецкая Александра Викторовна.
- •Содержание
- •Задание № 1
- •Пример расчета домашнего задания
- •1.1. Преобразование пассивного треугольника в эквивалентную звезду
- •2.2. Метод двух узлов
- •2.3. Расчет методом контурных токов
- •2.4. Определение токов в эквивалентном треугольнике исходной схемы
- •4. Баланс мощностей
- •5. Построение потенциальной диаграммы
- •2.1. Пример расчета домашнего задания № 2
- •2.2. Расчет токов методом проводимостей
- •2.3. Символический метод расчета цепей синусоидального тока
- •2.4. Расчет методом узловых потенциалов
- •2.5. Баланс мощностей
- •2.6. Построение векторной диаграммы
- •3.1. Пример расчета домашнего задания
- •3.1.1. Соединение в звезду с нулевым проводом
- •3.1.2. Соединение в звезду без нулевого провода
- •3.2. Расчет цепи при соединении в треугольник
3.1. Пример расчета домашнего задания
3.1.1. Соединение в звезду с нулевым проводом
Определяем полное сопротивление каждой фазы нагрузки:
Z a = Ra+ j( ХLa - ХCa) = Ra ± j Xa = Za e ja ;
Z b = Rb + j(XLb - XCb) = Rb ± j Xb = Zb e jb ; (3.1)
Z c = Rc + j(XLc - XCc) = Rc ± j Xc = Zc e jc .
Система фазных напряжений приемника имеет вид:
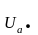 =
UA
e
=
UA
e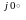 ;
; 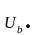 = UB
e
= UB
e
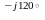 ;
;
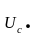 = UC
e
= UC
e
 .
(3.2)
.
(3.2)
По закону Ома определяется ток в комплексной форме в каждой фазе:
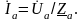 ;
;
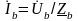 ;
;
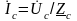 .
(3.3)
.
(3.3)
Ток в нейтральном проводе определяется по первому закону Кирхгофа:
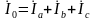 .
(3.4)
.
(3.4)
Активная
Р, реактивная Q и полная мощность нагрузки
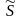 рассчитываются
по формуле (3.5):
рассчитываются
по формуле (3.5):
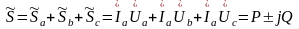 , (3.5)
, (3.5)
где
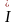
сопряженный комплекс тока (т.е. знак
перед j
показателем степени, изменяется на
противоположный).
сопряженный комплекс тока (т.е. знак
перед j
показателем степени, изменяется на
противоположный).
Строим векторную диаграмму напряжений и токов для схемы рис. 3.2, а, б по следующим формулам (3.6):
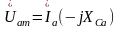 ;
; 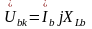 ;
; 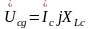 ;
(3.6)
;
(3.6)
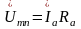 ;
; 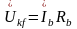 ;
; 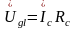 ;
;
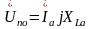 ;
; 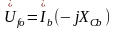 ;
; 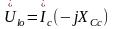 .
.

0'

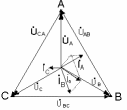
а) б)
Рис. 3.2. а) трехфазная схема при соединении звездой с нейтральным проводом б) векторная диаграмма
3.1.2. Соединение в звезду без нулевого провода
Определяем напряжение смещения нейтрали:
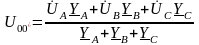 , (3.7)
, (3.7)
где
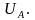 ,
,
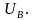 ,
,
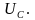
фазные напряжения источника; YA,
YB,
YC
комплексы полной проводимости фаз.
фазные напряжения источника; YA,
YB,
YC
комплексы полной проводимости фаз.
Определяем напряжения и токи в фазах нагрузки по второму закону Кирхгофа и по закону Ома (3.8), (3.9):
 =
=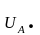
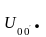 ;
;
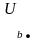 =
=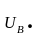
;
;
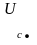 =
=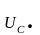
; (3.8)
; (3.8)
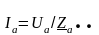 ;
;
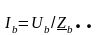 ;
;
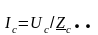 . (3.9)
. (3.9)
Делаем
проверку по первому закону Кирхгофа:
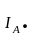 +
+
 +
+
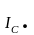 = 0.
= 0.
Строим векторную диаграмму напряжений и токов (рис. 3.3). Построение, как в предыдущем случае, начинаем с векторов фазных напряжений: сперва источника напряжения ( ; ; ), затем приемников( ; ; ), для чего строится напряжение смещения нейтрали .
Фазные
токи
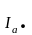 ;
;
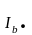 ;
;
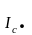 возникают под действием фазных напряжений
(
;
;
),
поэтому откладываются не относительно
точки О, а точки
возникают под действием фазных напряжений
(
;
;
),
поэтому откладываются не относительно
точки О, а точки
 (смещения нейтрали). Геометрическая
сумма векторов токов
;
;
должна равняться нулю. Определяем
активную, реактивную и полную мощность,
потребляемую нагрузкой (расчет ведется
аналогично предыдущему).
(смещения нейтрали). Геометрическая
сумма векторов токов
;
;
должна равняться нулю. Определяем
активную, реактивную и полную мощность,
потребляемую нагрузкой (расчет ведется
аналогично предыдущему).

Рис. 3.3. Векторная диаграмма для схемы при соединении в звезду без нейтрального провода.
3.2. Расчет цепи при соединении в треугольник
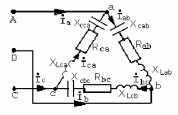
Рис. 3.4. Схема трехфазной цепи при соединении в треугольник.
Находим
линейные напряжения
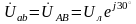 ,
,
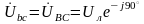 ,
,
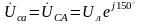 , (3.10)
, (3.10)
где
линейное напряжение должно быть
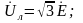 значение
значение
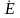 берется из условий задачи.
берется из условий задачи.
Определяем токи в фазах нагрузки по закону Ома:
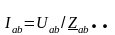 ;
;
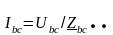 ;
; 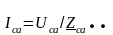 ; (3.11)
; (3.11)
где Zab; Zbc; Zca – сопротивление фаз нагрузки, соединенной в треугольник и численно равное нагрузке, принимаемой в предыдущих расчетах:
Zab = Za; Zbc= Zb; Zca=Zc. (3.12)
Линейные токи определяем по первому закону Кирхгофа:
=
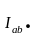
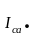 ,
=
,
=
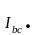
,
=
. (3.13)
,
=
. (3.13)
Так как цепь электропроводная, то сумма линейных токов равняется нулю:
Iл = 0; + + = 0. (3.14)
Расчет мощностей ведется аналогично предыдущему.
Построение векторной диаграммы проводим следующим образом (рис. 3.5).
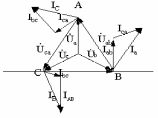
Рис. 3.5. Векторная диаграмма для схемы при соединении треугольником (рис.3.4)
На комплексной плоскости в масштабе строим систему фазных напряжений генератора ; ; . Соединив точки А, В, С, получим систему линейных напряжений генератора и фазных напряжений приемника Uab, Ubc, Uca. В точках А, В, С строим вспомогательные оси комплексной плоскости (действительную и мнимую).
На
этих осях из точки А откладываем вектор
тока
,
из точки В строим вектор тока
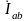 ,
из точки С строим
,
из точки С строим
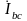 ,
т.е. строим фазные токи приемника так,
чтобы начало векторов напряжения и тока
одноименной фазы совпадали. По уравнениям
Кирхгофа строим векторы линейных токов.
,
т.е. строим фазные токи приемника так,
чтобы начало векторов напряжения и тока
одноименной фазы совпадали. По уравнениям
Кирхгофа строим векторы линейных токов.
ВОПРОСЫ К КОЛЛОКВИУМУ № 3
Анализ четырехпроводной и трехпроводной цепей при соединении симметричной и несимметричной нагрузки по схеме звезда. Анализ трехфазной цепи при соединении в треугольник.
ПРИЛОЖЕНИЕ 1

ПРИЛОЖЕНИЕ 11

Список рекомендуемой литературы
Касаткин А. С. Электротехника / А. С. Касаткин, В. М. Немцов. – М.: Издательский центр «Академия», 2008. – 544 с.
Рекус Г. Г. Общая. Электротехника и основы промышленной электроники / Г. Г. Рекус.. – М.: Высш. шк., 2008. – 416 с.
Новожилов О. П. Электротехника и электроника: учебник / О. П. Новожилов.. – М.: Гардарики, 2008. – 613 с.
4. Иванов И. И. Электротехника и основы электроники : учебник [Электронный ресурс] / И. И. Иванов, Г. И. Соловьев, В. Я. Фролов. – 7-е изд., перераб. и доп. – СПб. : Лань, 2012. – 736с. - Режим доступа: http://e.lanbook.com/books/element.php?pl1_cid=25&pl1_id=3190.
