2.1. Пример расчета домашнего задания № 2

Находим величины реактивных сопротивлений (2.1):

X_L = L = pf 10^–3 = 314 L10^–3 Ом,

X_C = 1/L = 1/(pC10^–6)= 10⁶/(314С) Ом, (2.1)

где L  индуктивность, мГн, С  емкость, мкФ. Только в этих случаях допускается округление до целых чисел.

2.2. Расчет токов методом проводимостей

Находим величины реактивных сопротивлений в каждой ветви Х = Х_L – X_C. Если Х(+), то характер результирующего реактивного сопротивления индуктивный, если Х()  емкостный. В одной из ветвей возможен резонанс, условием которого является равенство реактивных сопротивлений Х_C = X_L, при котором Х = 0.

Рассмотрим пример (рис. 2.1).

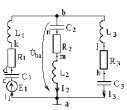
Рис. 2.1. Схема однофазной цепи переменного тока.

Составляем схему замещения, которая имеет вид, показанный на рис. 2.2.

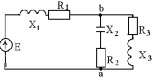
Z = R² +(X_L-X_C)² ;

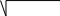
Z = R² + Х² . (2.2)

Рис. 2.2. Схема замещения.

Находим активные и реактивные проводимости параллельных ветвей. Параллельная ветвь 2 (Х₂  емкостный характер):

g₂= R₂ / (R₂² + Х₂²); b₂ =  X₂ / (R₂² + Х₂²). (2.3)

Параллельная ветвь 3 (Х₃ – индуктивный характер):

g₃ = R₃ / (R₃² + Х₃²); b₃ = Х₃ / (R₃² + X₃²). (2.4)

В результате преобразования схема будет иметь вид (рис. 2.3).

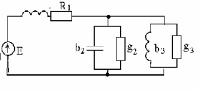
Y₂ = g₂² + b₂² ;

Y₃ = g₃² + b₃² . (2.5)

Рис. 2.3. Схема замещения после

преобразования параллельных ветвей

Определяем эквивалентные проводимости двух ветвей (рис.2.4):

g₂₃ = g₂ + g₃ ,

b₂₃ = b₃ – b₂ ,

Y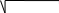 ₂₃ = g₂₃ + ₃₂₃ = Y_ab . (2.6)

Рис. 2.4.

Характер проводимости b₂₃ определяется по знаку b₂₃: при (+) характер индуктивный, при (–)  емкостный. Схема имеет вид, показанный на рис. 2.4.

На участке ab от проводимостей переходим к сопротивлениям, т.к. этот участок соединен последовательно с участком bс:

R_ab = g₂₃ /Y₂₃², X_ab = b₂₃ /Y₂₃². (2.7)

При переходе к сопротивлениям схема замещения приобретает вид, представленный на рис. 2.5, а).

а) б) в)

Рис. 2.5. Схемы замещения при переходе к сопротивлениям.

Определяем эквивалентное сопротивление схемы рис. 2.5, б) и 2.5, в):

R_экв = R₁ + R_ab; X_экв = X₁ + X_ab; ; (2.8)

_экв = arctg (X_экв / R_экв).

Вычисляем ток I₁ первой ветви и источника по закону Ома, а так же находим его активную I_1a и реактивную I_1p составляющие:

I₁ = E / Z_экв , I_1a=I₁cos_экв , I_1P=I₁sin_экв. (2.9)

Определяем напряжение на параллельном участке ab, его полную U_ab, активную U_ab,p и реактивную U_ab,p составляющие:

U_ab,aк = I₁R_ab; U_ab,p = I₁X_ab; 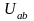= 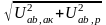, (2.10)

Вычисляем токи и углы сдвига фаз φ между токами и напряжениями в параллельных ветвях:

I­₂ = Y₂U_ab; I_2aк = g₂U_ab; I_2р = b₂U_ab; I₂ = ;

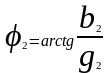; (2.11)

I₃ = Y₃U_ab; I_3aк = g₃U_ab; I_3р = b₃U_ab; I₃ = 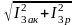; . (2.12)

Проверка по первому закону Кирхгофа:

I_1a = I_2a + I_3a; I_1р = I_2р + I_3р.

Значения модулей токов I₁, I_2, I₃ должны быть равны соответствующим значениям, полученным другими методами.