2.3. Расчет методом контурных токов

Расчет проводится в следующей последовательности:

а) выбираем направление контурных токов и положительные направления токов во всех ветвях (рис. 1.6):

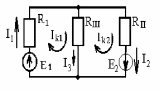
Рис. 1.6. Преобразованная схема с указанными направлениями контурных токов.

б) составляем систему из двух уравнений с двумя неизвестными:

I_k1R₁₁  I_k2R₁₂ = E₁₁ ,

 I_k1R₁₂ + I_k2R₂₂ = E₂₂ ; (1.8)

где R₁₂ = R₂₁  взаимные сопротивления контуров; R₁₁, R₂₂ — собственные сопротивления контуров, равные сумме сопротивлений соответствующего контура; E₁₁ , E₂₂  сумма ЭДС соответствующего контура.

Знак взаимного сопротивления определяется направлением контурных токов в нем. Если контурные токи во взаимном сопротивлении совпадают по направлению, то R₁₂ берется со знаком (+), если нет, то со знаком ().

Для схемы рис. 1.6 уравнения имеют вид:

I_k1(R_I + R_III )  I_k2R_III = E₁,

 I_k1R_III + I_k2(R_III + R_II ) = E₂. (1.9)

Если направление ЭДС совпадает с направлением контурного тока, то оно берется со знаком (+), если не совпадает, то со знаком ().

Решаем полученную систему уравнений с помощью определителей (1.10):

_



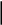
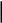R _I + R_III  R_III E₁  R_III

 R_III R_III + R_II ; E₂ R_III + R_II ;

_

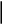R_I + R_III E₁

 R_III E₂ . (1.10)

Токи во внешних ветвях контуров равны соответствующим контурным токам, а в смежных  алгебраической сумме соответствующих контурных токов:

I_k1 = I₁ = _, I_k2 = I₂ = _ /1.11

Для схемы (рис. 1.6) I₃ = I_k1  I_k2, т.к. контурные токи в резисторе R_III направлены навстречу друг другу;

в) делаем проверку по первому закону Кирхгофа;

г) сравниваем токи, найденные методом контурных токов, с токами, найденными другими методами. Они должны быть равны.

2.4. Определение токов в эквивалентном треугольнике исходной схемы

С ИСПОЛЬЗОВАНИЕМ УРАВНЕНИЙ ВТОРОГО ЗАКОНА КИРХГОФА

Рис. 1.7. Исходная схема с пассивным треугольником.

Для схемы (рис. 1.7) уравнения второго закона Кирхгофа, с направлением обхода контуров по часовой стрелке имеют вид:

E₂ = I₂R₂ + I₆R₆  I₃R₃;

E₂  E₁ =  I₂R₂  I₁R₁  I₄R₄; (1.11)

0 = I₄R₄ + I₅R₅  I₆R₆.

Выражаем из (1.11) недостающие токи:

;

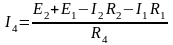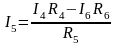; (1.12)

.

Если в результате решения этих уравнений токи имеют отрицательное значение, это означает, что действительное направление токов противоположно выбранному.

3. определение тока I_K (к = 5) Методом эквивалентного генератора

Определяем ЭДС эквивалентного генератора Е_экв, то есть напряжение между узлами, к которым подключена n_k (к=5) ветвь. Для этого убираем ветвь с R₅ (рис. 1.8) и находим токи в оставшейся схеме любым ранее рассмотренным методом.

Например, в схеме на рис. 1.8 находим токи методом двух узлов.

Напряжение между узлами 0 и 2:

U₀₂ = [(E₁(R₁+R₄))  (E₂/R₂)]/[(1/(R₁+R₄))+(l/R₂)+(l/(R₃+ R₆)). (1.12)

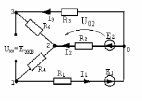
Рис. 1.8.

По закону Ома находим токи в ветвях:

I₁ = (E₁U₀₂ ) / (R₁+R₄);

I₂ =(E₂ + U₀₂ ) / R₂; (1.13)

I₃ = U₀₂ / (R₃ + R₆).

Определяем Е_экв = U_xx = _ _, (1.14)

где _ = 0; _=  I₃ R₃ ; _ = I₁R₁  E₁.

Чтобы найти внутреннее сопротивление эквивалентного генератора относительно зажимов (3) и (1), закорачиваем все ЭДС и рассчитываем схему методом эквивалентных преобразований (рис. 1.9).

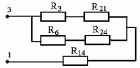
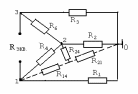
а б

Рис. 1.9. Схема для расчета методом

эквивалентных преобразований.

Сопротивления схемы отыскиваем следующим образом:

R₂₁ = R₂ R₁/(R₁+ R₂+ R₄),

R₁₄ = R₄R₁/(R₁+ R₂+ R₄), (1.15)

R₂₄ = R₂R₄/(R₁+ R₂+ R₄),

R_экв = R₁₄+[(R₃+R₂₁)(R₆+R₂₄)/(R₃+R₂₁+R₆+R₂₄)].

Находим ток в пятой ветви по закону Ома: I₅ = E_экв /(R_экв + R₅).

Значение тока I_k (I₅) должно соответствовать значению тока в этой ветви, найденному другими методами. Значения токов, вычисленные разными методами, запишем в табл. 1.2. Погрешность расчета не должна превышать 2 %.

Таблица 1.2

Метод расчета	I1	I2	I3	I4	I5	I6
Метод наложения
Метод узловых напряжений
Метод контурных токов
Метод эквивалентного генератора