- •Механика.
- •Вопрос.2.Скорость и ускорение при криволинейном движении. Нормальное и тангенсальное (касательное) ускорение.
- •Вопрос. Движение точки по окружности. Угловая скорость и угловое ускорение. Вектор угловой скорости.
- •Вопрос. Динамика.
- •Основные законы:
- •Постулаты преобразования Лоренца.
- •Взаимосвязь массы и энергии. Реалитивийские выражения для кинематической энергии
- •Основные соотношения мкт
- •Внутренние трение.
- •Обратимые и необратимые процессы. Тепловые и двигатели и холодил. Машины
- •Распределение молекул по скоростям, распределение Максвела
Обратимые и необратимые процессы. Тепловые и двигатели и холодил. Машины
Термодинамический процесс совершаемой системы называется обратимым если после него возможно обратить систему и все взаимодействующие с ней тела в их начальное состояние. В идеале обратимых процессов не существует.
Круговой процесс – это процесс при котором система возвращается в исходное состояние.
Тела совершающие кругово роцесс и обменивающиеся энергией с другими телами называется рабочим телом. Обычно таким телом является газ.
Круговые процессы лежат в основе работы всех тепловых машин. А именно ДВС, паровых и газовых турбин, холодильных машин и тд. Поэтому изучение различных свойств круговых процессов – основная задача термодинамики.
За счет подвода количества теплоты. Газ совершает положительную работу где теплота от внешних источников поступает к рабочему телу. При этом оно выполняет положительную работу. Такой цикл называется прямым. Q=A>0
За счет работы внешних сил Q<0 от газа забирается теплота. Принцип работы холодильных машин. Q=A<0
Цикл карно
Рассмотрим подробно круговой процесс, разработанный французский инженером Карно . этой прямой цикл, совершающий идеальным газом. При этом коэфф. полезного действия этого цикла явл.макс.

1-2 изотермическое расширение
2-3 адиабатное расширение
3-4 изотермическое сжатие
4-1 адиабатное сжатие
1-2: газ находится в тепловом контакте и равновесии с телом имеюший Т1, который называетс я нагревательным. При этом нагреватель ожидает кол-во теплоты Q1в 2-3: газ полностью теплоизолирует от нагревания и заключает адиабатную оболочку. Затем газ (3-4)приводится в теловой контакт другим теплом (Т2) при этом Т2<Т1 назыв. холодильником(теплоприемником).Состояние 4 газа полностью изолируте и адиобат. Теплота не отдается.
При
любом круговом движении
 |
|
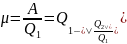 -
коэфф.
полезного действия для любой тепловой
машины
-
коэфф.
полезного действия для любой тепловой
машины


 -
макс.кпд. для идеальных газов
-
макс.кпд. для идеальных газов
 -Из
урав-ияПаусона
-Из
урав-ияПаусона
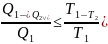 |
|
Второе начало закона термодинамики
1 закон термодин это закон сохр энергии и о превращ энергии.но 1 з-н не позволяет определить направл протекания процессов. В самом деле процесс самопроизв передачи теплоты от холодн к горяч и противореч 1-му з-ну ,если только уменьш внутр энергии 1-ого тела =энергии получ 2-ым телом . однако показыв что такой процесс не происх.
Пример:при описан расколённого куска железа в холодн воду никогда не происх дальнейшее нагревание железа за счёт соответств охлажд воды. И это не искл 1 з-н т.е не искл возможн такого процесса единственным результатом которого было бы привращ тепл получ от некоторого тела эквивалентн. ей работу.
Сущ невозможен процесс единств результатом которого явл передача теплоты от холод к горяч
Закон сохранения мех. энергии Закон сохранения энергии является следствием фундаментального свойства времени – однородности. Однородность времени заключается в том, что физические законы инвариантны относительно выбора начала отсчета времени. Во многих случаях потенциальная энергия является функцией только одной координаты U=U(x). График зависимости U от какого-то одного аргумента называется потенциальной кривой. Анализ потенциальных кривых позволяет определить характер движения тела. Особый случай представляют консервативные и замкнутые системы, в которых E=U+T=const.
Статически и термодиномически. Равновесия состояния диаграмма состояния Статистический метод — это метод исследования систем из большого числа частиц, оперирующий статистическими закономерностями и средними (усредненными) значениями физических величин, характеризующих всю систему. Этот метод лежит в основе молекулярной физики — раздела физики, изучающего строение и свойства вещества исходя из молекулярно- кинетических представлений, основывающихся на том, что все тела состоят из атомов, молекул или ионов находящихся в непрерывном хаотическом движении. В дальнейшем мы будем использовать термин "молекула" имея ввиду мельчайшую структурную единицу (элемент) данного вещества. Термодинамический метод — это метод исследования систем из большого числа частиц, оперирующий величинами, характеризующими систему в целом (например, давление, объем, температура) при различных превращениях энергии, происходящих в системе, не учитывая при этом внутреннего строения изучаемых тел и характера движения отдельных частиц. Этот метод лежит в основе термодинамики — раздела физики, изучающего общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями.
Явление переноса |
15:10:15 |
|
|
|
|
|
Механи́ческое равнове́сие — состояние механической системы, при котором сумма всех сил, действующих на каждую её частицу, равна нулю и сумма моментов всех сил, приложенных к телу относительно любой произвольно взятой оси вращения, также равна нулю. В состоянии равновесия тело находится в покое (вектор скорости равен нулю) в выбранной системе отсчета либо движется равномерно прямолинейно или вращается без касательного ускорения. |
|
|
Среднее число столкновений и средняя длина свободного пробега Средние
скорости молекул, газа очень велики
- порядка сотен метров в секунду при
обычных условиях. Однако процесс
выравнивая неоднородности в газе
вследствие молекулярного движения
протекает весьма медленно. Это
объясняется тем, что молекулы при
перемещении испытывают соударения
с другими молекулами. При каждом
соударении скорость молекулы изменяется
по величине и направлению. Вследствие
этого, скорость, с которой молекула
диффундирует из одной части газа в
другую, значительно меньше средней
скорости молекулярного движения. Для
оценки скорости движения молекул
вводится понятие средней длины
свободного пробега. Таким образом,
средняя дли свободного пробега Для
определения
вычислим
сначала среднее число соударений
Молекулы,
с которыми соударяется выбранная
молекула, в первом приближении считаем
неподвижными и принимаем их за
сферические тела радиуса r. Пусть
выбранная молекула движется вправо
из положения
Если концентрация молекул n , то внутри рассмотренного цилиндра находится число молекул, равное
Это число и определяет среднее число соударений за единицу времени. Предположение
о том, что все молекулы, кроме одной,
неподвижны, является, конечно не
верным. В действительности все молекулы
движутся, и возможность соударения
двух частиц зависит от их относительной
скорости. Поэтому вместо
среднеарифметической скорости
должны
входить средняя относительная скорость
молекул Средний
путь, проходимый молекулой за единицу
времени, численно равен
.
Поэтому средняя длина свободного
пробега равна Таким
образом, средняя длина свободного
пробега
не
зависит от температуры газа, т.к. с
ростом температуры одновременно
возрастают и
,
и
.
При подсчете числа соударений и
средней длины свободного пробега
молекул за модель молекулы было
принято шарообразное упругое тело.
В действительности каждая молекула
представляет собой сложную систему
элементарных частиц и при рассмотрении
упругого соударения молекул имелось
в виду, что центры молекул могут
сблизиться до некоторого наименьшего
расстояния. Затем возникает силы
отталкивания которые вызывают
взаимодействие, подобное взаимодействию
при упругом ударе. Среднее расстояние
между центрами молекул, взаимодействующих,
как при упругом ударе, называют
эффективным диаметром
Инерция из приобразования Лоренца. Преобразованиями Лоренца в физике, в частности, в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично, преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.Чтобы явно различить преобразования Лоренца со сдвигами начала отсчёта и без сдвигов, когда это необходимо, говорят о неоднородных и однородных преобразованиях Лоренца.Преобразования Лоренца векторного пространства (т.е. без сдвигов начала отсчёта) образуют группу Лоренца, а преобразования Лоренца аффинного пространства (т.е. со сдвигами) — группу Пуанкаре, иначе называемую неоднородной группой Лоренца.С математической точки зрения преобразования Лоренца — это преобразования, сохраняющие неизменной метрику Минковского, то есть, в частности, последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой (другими словами, преобразования Лоренца — это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса к другому, то есть аналог поворота координатных осей для пространства-времени). В математике или теоретической физике преобразования Лоренца могут относиться к любой размерности пространства.Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени.Следует заметить, что лоренц-ковариантны не только фундаментальные уравнения (такие, как уравнения Максвелла, описывающее электромагнитное поле, уравнение Дирака, описывающее электрон и другие фермионы), но и такие макроскопические уравнения, как волновое уравнение, описывающее (приближенно) звук, колебания струн и мембран, и некоторые другие (только тогда уже в формулах преобразований Лоренца под следует иметь в виду не скорость света, а какую-то другую константу, например скорость звука). Поэтому преобразования Лоренца могут быть плодотворно использованы и в связи с такими уравнениями (хотя и в довольно формальном смысле, впрочем, мало отличающемся — в своих рамках — от их применения в фундаментальной физике).
Связь между импульсом и полной энергии частиц. Полная энергия и импульс частицы определяются соотношениями E = mc2γ, (3) p = γmv = vE/c2. Полная энергия и импульс частицы зависят от системы отсчетаю. Масса не меняется при переходе от одной инерциальной системы отсчета к другой. Она является лоренцевым инвариантом. Полная энергия импульс и масса связаны соотношением E2 - p2c2 = m2c4, (4) где E, р и m - полная энергия, импульс и масса частицы, с - скорость света в вакууме. Из соотношения (3) и (4) следует, что если энергия E и импульс p измеряются в двух различных системах движущихся друг относительно друга со скоростью v, то энергия и импульс будут иметь в этих системах различные значения. Однако величина E2 - p2c2, которая называется релятивистский инвариант, будет в этих системах одинаковой. Полная и кинетическая энергия связаны между собой соотношением Е = T + Е0 = Т + mc2, Т = Е - mc2, (5) где T - кинетическая энергия частицы, Е0 - энергия покоя частицы. Из (4) и (5) можно получить соотношение связывающее импульс p и кинетическую энергию T частицы p = (T2 + 2Tmc2)1/2/c. (6) Можно выделить два предельных случая 1. Ультрарелятивистский. Кинетическая энергия частицы много больше ее энергии покоя T » mc2 p = T/c или T = cp. (7а) 2. Классический. Кинетическая энергия частицы много меньше ее энергии покоя T « mc2 p = (2Tm)1/2 или T = p2/2m.
|
|
Диаграмма состояния (фазовая диаграмма), графическое изображение всех возможных состояний термодинамической системы в пространстве основных параметров состояния - температуры Т, давления р и состава х (обычно выражаемого молярными или массовыми долями компонентов). Для сложных систем, состоящих из многих фаз и компонентов, построение диаграмма состояния является единственным методом, позволяющим на практике установить, сколько фаз и какие конкретно фазы образуют систему при данных значениях параметров состояния. Каждое реально существующее состояние системы на диаграмме состояния изображается так называемой фигуративной точкой; областям существования одной фазы отвечают участки пространства (на трехмерных диаграммах состояния) или плоскости (на двухмерных диаграммах состояния), условиям сосуществования фаз соответствуют поверхности или линии; изменение фазового состояния системы рассматривается как движение фигуративной точки на диаграмме состояния |
|
|