Основные соотношения мкт

МКТ пользуется моделью идеального газа удовлетворяющие следующие условия :

1) пренебрегается собственный объемом молекулы

2) пренебрегается силами взаимодействия между молекулами

3)столкновение молекулы между собой и со стенками молекулы абсолютно упругое

На основе этой модели выводится основное уравнение МКТ идеального газа

Где:

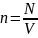-концентрация молекул

-Средняя кинетическая энергия поступательного движения одной молекулы

-масса молекулы

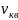-средняя квантовая скорость

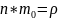- плотность

Моль-количество вещества в котором находится столько молекул сколько в 12г углерода

N=6.023*

Существует Больцмоноское выражение дл средней кинетической энергии

где

К=1.38*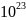

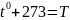
P=nKT

Температура -это мера средней кинетической энергии

K*N=8.31 =R

Внутренние трение.

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате работа, затрачиваемая на это перемещение, рассеивается в виде тепла.

Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Различают динамическую вязкость (единица измерения в Международной системе единиц (СИ) — Па·с, в системе СГС — пуаз; 1 Па·с = 10 пуаз) и кинематическую вязкость (единица измерения в СИ — м²/с, в СГС — стокс, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести. Прибор для измерения вязкости называется вискозиметром.

Переход вещества из жидкого состояния в стеклообразное обычно связывают с достижением вязкости порядка 10¹¹−10¹² Па·с.

Сила вязкого трения

Сила вязкого трения F, действующая на жидкость, пропорциональна (в простейшем случае сдвигового течения вдоль плоской стенки^[1]) скоростиотносительного движения v тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h:

Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости.

Качественно существенное отличие сил вязкого трения от сухого трения, кроме прочего, то, что тело при наличии только вязкого трения и сколь угодно малой внешней силы обязательно придет в движение, то есть для вязкого трения не существует трения покоя, и наоборот — под действием только вязкого трения тело, вначале двигавшееся, никогда (в рамках макроскопического приближения, пренебрегающего броуновским движением) полностью не остановится, хотя движение и будет бесконечно замедляться.

Вязкость газов

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

,

где   — средняя скорость теплового движения молекул,   − средняя длина свободного пробега. Из этого выражения в частности следует, что вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность   прямо пропорциональна давлению, а   — обратно пропорциональна. Такой же вывод следует и для других кинетических коэффициентов для газов, например, для коэффициента теплопроводности. Однако этот вывод справедлив только до тех пор, пока разрежение газа не становится столь малым, что отношение длины свободного пробега к линейным размерам сосуда (число Кнудсена) не становится по порядку величины равным единице; в частности, это имеет место в сосудах Дьюара (термосах).

С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа  , растущей с температурой как 

 Число степеней свободы. Закон о равномерном распределении энергии после свободы

Ч исло степеней свободы – это число независимых переменных (координат), полностью определяющих состояние системы(число независимых движений). 1) одноатомная

i =1

П

2) двухатомная

i= 3 + 2 = 5

П Вр

3) трехатомная

i= 3 + 3 = 6

П Вр

_iп =3 Е_к,п = 3/2 кТ; на 1 степень свободы приходится средняя энергия

Таким образом,

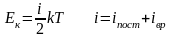
Внутренняя энергия идеального газа – суммарная кинетическая энергия движения всех молекул

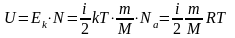
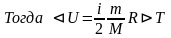
_{Внутренняя энергия от вида не зависит}

Работа газа при изменении объёма систем. Количество теплоты. Первый закон термодинамики

Работа газа - при изменении объема системы количество теплоты .Первый закон термодимамики.

Найдет общий виде работу совершаемым газом при изменении его объема для этого рассмотрим газ в цилиндре под поршнем

P=const

ᵟa=Fdx=ps*dv

SA=p*dv

Полная работа газа при изменении его объема 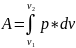– Работа газа при изменении системы

Результат интегрирования определяет характер зависимости между давлением и объемом газа.

dv>0 ᵟA>0

Dv<0 ᵟA<0

Количество

Количество теплоты –величина энергии переданной системе виде теплового движения атомов или молекул

-работа за системой газов

-Первый закон термодинамики

Если система периодически возрастает в состояние

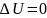
Q=A

Нельзя построить периодически действующий двигатель совершал большую работу им количество энергии

Применение 1-го Закона термодинамики изопроцесс.

1) T=const изатермический

Q=∆u+A , ∆T=0 , ∆u=0

Q=A

2) V=const изахорный

Q=∆u+A, dV=0, A=0

3) p=const изобарный

Q=∆u+A, ∆u≠0, A≠0

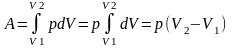
Теплоёмкость газа зависимость теплоёмкости от вида процесса

Тплоёмкость-это кол-во теплоты, которое необходимо сообщить системе, чтобы изменить Т на 1к

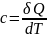, различают удельную и молекулярную теплоёмкость

Молярная: (теплоёмкость 1 моль)= =

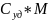
Кол-во теплоты зависит от вида процесса, при Т=const dT=o

C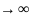

При V=const найдём молекулярную теплоёмкость

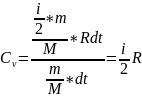
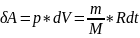
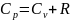-уравнение Роберта Майера

-постоянная Пуасона(Адеабата)

Адиабатный процесс уравнение Пуассона

Процесс, при котором отсутствует теплообмен между системой и окружающей средой

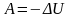(резкое расширение)

Внутреннее расширение уменьшается, температура газа будет понижаться.

Если над газом совершается работа

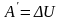
внутренняя энергия увеличивается - температура повышается.

Для 1 моля моля при адиабатном процессе:

,

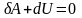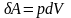
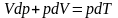
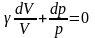
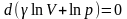
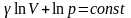
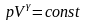- уравнение Пуассона

,

Адиабата идёт круче изотермы. Это связано с тем, что при T=const(1,2) рост давления обусловлен только уменьшением V.

При адиабатном сжатии (1,3) давление растет быстрее не только за счет уменьшения V, но и повышения T.

При изотермическом расширении (1,5) уменьшения V обусловлено только увеличение V.

При адиабатном расширении уменьшение давления обусловлено не только увеличением V, но и понижением T.

Поэтому Р падает быстрее

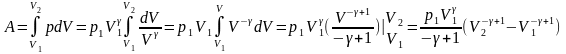
Уравнения состояния реальных газов(Уравнение Ван-дер-Ваальса)

Уравнение Менделеева – Клапейрона для одного моля вещества:

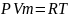
Хорошо описывает такое поведение и реальных газов при малых плотностях(при небольших давлениях) и достаточно высоких температур.С повышением давления и умееньшением температуры наблюдается значительные отспуления от этого уравненияю. Эти отклонения не представляются удивительными,посколкьу при увеличении плотности(давления) начинают играть всё большую роль собственный обьем молекул,а так же взаимодействие между ними. Молекулы идеального газа,заключенные в некотором сосуде,может находитсья в любой его точке,и для него доступен весь обьем сосуда.Молекула p газа не может находиться в тех местах сосуда,где находяться остальные N-1 молекулыю.Ей доступна лишь часть его его объема=Vm-a, где a-попрака Ван-дер-Ваальса объема.Давление газа на стенку сосуда есть результат многочисленных столкновенний молекул с поверхностью стенки,поэтому: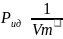 ,то есть ещё силы взаимодействия.

; , где b-поправка Ван-дер-Ваальса силу взаимодействия.

Учитывая,что ; , Получим

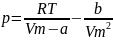
Окончательное уравнение: 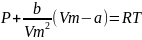–Уравнение Ван-дер-Ваальса для 1 моля. ---- (1)

; ;

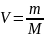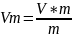
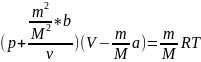-Уравнение Ван-дер-Ваальса для некоторой массы газа.

Раскрыв скобки формулы 1,получим

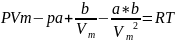
---(2)

Мы получили уравнение 3-ей степени относительного объема.Коэффициент уравнения от давления P,T и химической природы газа.В зависимости от P и T для данного газа,уравнение может иметь 1 действительный корень,либо 3 действительных корня.

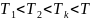
При имеется область состояния, где каждому Р соответствует 3 точки ихотерны,т.е при различных изотермических состояниях(Va,Vk,Vc).

По мере повышения температуры,эти 3 точки сближаются и при температуре 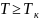сливаются в 1 точку К, кот. Является точкой перегиба изотермы Тк.При Т>Тк изотермы будут близки к изотермам идеального газа

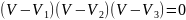
T=Tк / точка К называется Критической

Р=Рк

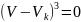
Если раскроем уравнение ,то (3)

Сравниваем (2) и (3),получим:

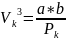; ; . Vк=3а

Критическая точка соотвествует состоянию вещества в 2-х фазах,левее точки-жидкое состояние,правее-газообразное