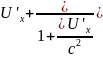- •Механика.
- •Вопрос.2.Скорость и ускорение при криволинейном движении. Нормальное и тангенсальное (касательное) ускорение.
- •Вопрос. Движение точки по окружности. Угловая скорость и угловое ускорение. Вектор угловой скорости.
- •Вопрос. Динамика.
- •Основные законы:
- •Постулаты преобразования Лоренца.
- •Взаимосвязь массы и энергии. Реалитивийские выражения для кинематической энергии
- •Основные соотношения мкт
- •Внутренние трение.
- •Обратимые и необратимые процессы. Тепловые и двигатели и холодил. Машины
- •Распределение молекул по скоростям, распределение Максвела
Постулаты преобразования Лоренца.
Пусть в системе (К): (х, у, z) и (К`) : (х`,у`,z`), которые движутся со скоростью V = const относительно (х). Пусть момент времени t = t` = 0, тогда начала координат совпадают излучается световой импульс (С), согласно 2-му постулату с =const, поэтому: x = c · t; x` = c · t`.
В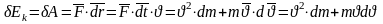 ычитаем
x`
- x
= с (t`
- t).
Т.к. x`
≠ x,
то => t`
≠ t.
Вывод:
отсчёт времени имеет относительный
характер ( а в классической механики
t`
= t).
Эйнштейн
показал, что в теории относительности
классические преобразования Галлелея
описывающие переход от одной ИСО в
другой, должны быть заменены другими
преобразованиями (Лоренц), удовлетворяющие
постулатам Эйнштейна.
Они имеют вид:
ычитаем
x`
- x
= с (t`
- t).
Т.к. x`
≠ x,
то => t`
≠ t.
Вывод:
отсчёт времени имеет относительный
характер ( а в классической механики
t`
= t).
Эйнштейн
показал, что в теории относительности
классические преобразования Галлелея
описывающие переход от одной ИСО в
другой, должны быть заменены другими
преобразованиями (Лоренц), удовлетворяющие
постулатам Эйнштейна.
Они имеют вид:
K`→K
|
K → K`
|
Из преобразования Лоренца, вытекает, что V<<C; β – можно пренебречь. Они переходят в классические преобразования Галилея.
При V>C, выражение теряют физический смысл, преобразования Лоренца становятся мнимыми. Это находится в свою очередь в соответствии с тем, что движение со скоростью больше скорости света в вакууме невозможно.
Из преобразований Лоренца следует очень важный вывод о том, что как расстояние, так и промежуток времени между двумя событиями, при переходе от одной ИСО в другую ИСО меняются.
Видим, что как пространственные так и временные координаты, не являются независимыми, поскольку закон преобразования координат входит время, а в законах преобразования времени, входит пространственная координата, т.е. устанавливается взаимосвязь пространства и времени.
Таким образом, теория Эйнштейна оперирует не с трёхмерным пространством к которому присоединяется понятие времени, а рассматривается неразрывно связанные пространственные и временные координаты оперируя четырёхмерным пространством.
Закон сложения скоростей релиатевинской механики
Пусть
![]() К’ относительно К. U
скорость точки относительно К
соответственно U’
скорость этой точки относительно К ‘:
К’ относительно К. U
скорость точки относительно К
соответственно U’
скорость этой точки относительно К ‘:
 = dx / dt
dx=
= dx / dt
dx=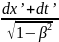 =
=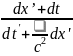 =
=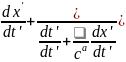
 =
= dt=
dt=
= |
U’=C’;
=C=>U=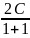 =C
=C
Реалитевиский импульс. Уравнения движения реалитивиской частицы
Согласно
классич. Механике м асса тела является
постоянной, однако к 19столетию на ….
Было установлено, что масса тела
возрастает с увеличением скорости
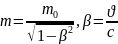 ,
,
где
 -масса
покоя
m-релятив.
Масса.
-масса
покоя
m-релятив.
Масса.
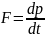
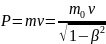 – релятивистский
импульс
– релятивистский
импульс
Тогда основное ур-е релятивистской мех-и:

В силу однородности пространства в релятив. механике также выполняется закон сохранения релят. импульса: релятив. импульс замкнутой системе сохраняется, т.е. не изменяется с течением времени. Из этого закона следует закон релятив. массы, а именно системы при любых процессах происходящих в ней сохраняется, т.е. не изменяется с течением времени.
Взаимосвязь массы и энергии. Реалитивийские выражения для кинематической энергии
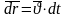
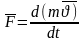


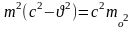

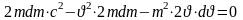 (сократим
на 2m)
(сократим
на 2m)
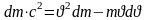


 =>
=>
 =>
=>
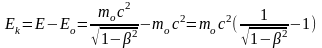
Связь
между импульсом и полной энергией
частиц


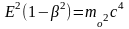









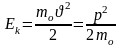

Из
сравнения, что импульс
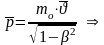
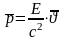
С
другой стороны
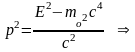
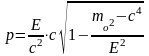

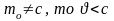


 .
. .
.