Механика.

Вопрос.1. Физические модели: материальная точка, система отсчета, система материальных точек, абсолютно твердое тело.

Кинетическое описание движения. Материальная точка – тело размерами которого можно принебречь в условиях данной физической задачи (когда размеры тела на много меньше расстояния до системы отсчета). Если размерами тела нельзя пренебречь, то тело разбивается на бесконечно малые точки. Размерами можно пренебречь, то говорят о системе материальных точек.

И зная движение каждой материальной точки системы можно судить о движении тела в целом.

Обсолютно-твердое тело: тело деформации которого можно пренебречь. Любое движение можно разложить на 2 основных движения: а) поступательное; б) вращательное. Поступательное когда любая прямая связанная с твердым телом при его движении, остается параллельной самой себе.

Поступательное движение может быть криволинейным. При этом любая точка твёрдого тела движется с одинаковой по модулю скоростью.

Вращательное: когда все точки твёрдого тела движутся по окружностям в центре которых лежат на одной прямой называемой осью вращения. Ось вращения может лежать вне твердого тела.

Любое движение происходит в пространстве и во времени, поэтому для описания движения используют систему координат. Материальная точка описывает траекторию.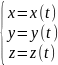 - кинетическое описание движения. Положение материальной точки в любой момент времени, если будем знать, можно определить зная как координаты зависят от времени. Исключая (t) – время (параметр) можно определить траекторию движения.

.

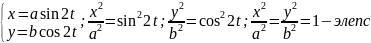Есть равносильное описание движения, а именно движение можно описать с помощью радиуса вектора ( . 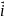, ,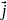 - единичные вектора направленные по соответствующим координатам.

В зависимости от формы траектории движение может быть: прямолинейным и криволинейным.

Прямолинейное движения частные случаи криволинейным движениям, когда радиус кривизны R=∞.

Вопрос.2.Скорость и ускорение при криволинейном движении. Нормальное и тангенсальное (касательное) ускорение.

Мгновенное значение скорости в точке А.

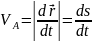
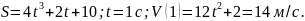
Если скорость какой-то функции от времени V=V(t) элементарный путь будет равно ds=V(t)·dt, тогда пройденый путь

Если скорость V =const, то S=V·Δt

При прямолинейном движении быстрота изменения скорости (V) характерная ускорением, т.е. изменение величины скорости в единицу времени. Вобщем случае при произвольно криволинейного движения вектор скорости 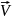будет характеризоваться векторным ускорением. В дальнейшим будем расчленять на две состовляющие харакиеризующие изменение скорости по величине и по направлению, если - изменение скорости за время Δt, то 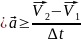- среднее ускорение за время Δt.

Тогда ускорение в какой-то конкретный момент времени

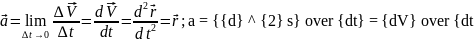
Пусть

Тогда:

a_n – характеризует изменение скорости по направлению тангенсальное ускорение; a_τ – характеризует изменение величины скорости. 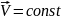, тогда a_n=0; a_τ=0.

Примем.

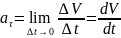; Если движение по окружности с постоянной по модулю скоростью направление не меняется a_n≠0; a_τ=0; a_n=V²/r; r – радиус кривизны траектории; - направленно по касательной траектории.

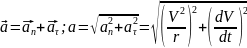- полное ускорение.