2.1 Определение размера представительной выборки

Данная задача решается тогда, когда необходимо определить размер выборки n, достаточный для получения математического ожидания результатов испытаний с заданной доверительной вероятностью p и относительной погрешностью , равной отношению доверительного интервала случайной величины к её математическому ожиданию.

При относительно небольших размерах выборок для построения доверительного интервала математического ожидания используют распределение Стьюдента

(2.3)

где - среднее значение выборки;

- математическое ожидание случайной величины;

- дисперсия наблюдений в выборке.

Распределение Стьюдента зависит только от числа степеней свободы f, с которым была определена выборочная дисперсия . При больших f распределение Стьюдента приближается к нормальному. Вероятность того, что случайная величина попадёт в заданный интервал … 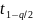, определяется выражением

P( ≤ t ≤ ) = 1 – q (2.4)

где q – уровень значимости.

Распределение Стьюдента симметрично относительно нуля, поэтому

(2.5)

Учитывая симметрию t-распределения, часто пользуются обозначением , где f - число степеней свободы, а р – вероятность того, что t находится за пределами интервала ( … ).

На основании изложенного математическое ожидание определяется неравенством

- ≤ + (2.6)

Значения квантилей для для различных f и q табулированы.

Выражение (2.6) позволяет производить интервальную оценку случайной величины при условии, что по физическому смыслу математическое ожидание имеет ограничение сверху и снизу. Если имеет только одностороннее ограничение, то при достоверной вероятности p=1-q оценка сверху либо снизу производится по условиям:

+ (2.7)

- (2.8)

Здесь при выборе табличного значения критерия Стьюдента уровень значимости q удваивается.

С учётом изложенного для определения размера представительной выборки может быть применён следующий итерационный алгоритм:

1. задать исходное значение числа наблюдений в выборке n;

2. рассчитать по формуле (2.1) среднее значение , а по формуле (2.2) дисперсию ;

3. рассчитать абсолютное значение возможного интервала изменения случайной величины

(2.9)

4. определить величину коэффициента Стьюдента, соответствующую возможному интервалу

t= ; (2.10)

5. с учетом физического смысла ограничений, налагаемых на математическое ожидание оцениваемого параметра, для соответствующего уровня значимости q и числа степеней свободы f=n-1 принять табличное значение критерия Стьюдента :

6. проверить выполнение неравенства

t < (2.11)

Если условие (2.11) выполняется, то принятый размер выборки не удовлетворяет решению задачи и должен быть увеличен.

2.2 Проверка гипотезы равноточности двух рядов результатов испытаний

К решению этой задачи прибегают, например, при исследовании влияния на результаты испытаний двух различных систем измерения либо при анализе воспроизводимости результатов эксперимента. На основе проверки гипотезы равноточности двух рядов результатов испытаний можно выявить значимость изменения какого-либо качественного фактора, сделать заключение об адекватности полученной математической модели эксперименту.

Для решения задачи используется дисперсионное отношение оценок большей дисперсии к меньшей (коэффициент Фишера)

F=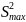 / (2.12)

Если результаты испытаний распределены по нормальному закону, то проверка гипотезы сводится к проверке неравенства

F ≤ (2.13)

где - табличное значение критерия Фишера для вероятности и чисел степеней свободы , .

При выполнении условия (2.13) гипотеза равноточности двух рядов результатов испытаний принимается.