283

МОДУЛЬ 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ 201

ЛЕКЦИЯ 2.1. ПЕРЕМЕННАЯ ВЕЛИЧИНА. ФУНКЦИЯ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СПОСОБЫ ЗАДАНИЯ. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ, ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ, ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ, ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ, ОДНОСТОРОННИЕ ПРЕДЕЛЫ 201

2.1.1. Переменная величина 202

2.1.2. Функция одной и нескольких переменных 203

2.1.3. Способы задания функции 206

2.1.4. Основные свойства функции 210

2.1.5. Предел переменной величины и последовательности 218

2.1.6. Предел функции 220

ЛЕКЦИЯ 2.2. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ, СВОЙСТВА. ТЕОРЕМЫ О ПРЕДЕЛАХ И ИХ ПРИМЕНЕНИЕ. ПРИЗНАКИ СУЩЕСТВОВАНИЯ ПРЕДЕЛОВ. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ. СРАВНЕНИЕ И ЭКВИВАЛЕНТНОСТЬ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ 225

2.2.1. Бесконечно малые и бесконечно большие функции, свойства 226

2.2.2. Теоремы о пределах 234

2.2.3. Признаки существования пределов 241

2.2.4. Замечательные пределы 243

2.2.5. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые 249

ЛЕКЦИЯ 2.3. ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ. ОПРЕДЕЛЕНИЯ ПРОИЗВОДНОЙ И ЧАСТНЫХ ПРОИЗВОДНЫХ, ИХ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ, ТАБЛИЦА ПРОИЗВОДНЫХ 254

2.3.1. Задачи, приводящие к понятию производной 255

2.3.2. Определения производной и частных производных, их геометрический смысл 258

2.3.3. Правила дифференцирования 264

2.3.4. Производная сложной функции 266

2.3.5. Производная обратной функции 269

2.3.6. Таблица производных 271

ЛЕКЦИЯ 2.4. ПРОИЗВОДНАЯ НЕЯВНО ЗАДАННОЙ И ПАРАМЕТРИЧЕСКИ ЗАДАННОЙ ФУНКЦИЙ 272

2.4.1. Производная неявно заданной функции 272

2.4.2. Производная функции, заданной параметрически 276

2.4.3. Логарифмическое дифференцирование 276

2.4.4. Производные высших порядков 278

МОДУЛЬ 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ЛЕКЦИЯ 2.1. ПЕРЕМЕННАЯ ВЕЛИЧИНА. ФУНКЦИЯ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СПОСОБЫ ЗАДАНИЯ. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ, ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ, ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ, ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ, ОДНОСТОРОННИЕ ПРЕДЕЛЫ

Прогнозируемые результаты обучения в виде составляющих предметных компетенций:

• Базовые понятия:

-– функция одной и нескольких переменных,

– способ задания функции,

– предел последовательности,

– предел функции в точке,

– односторонние пределы,

• Базовые операции:

– определение способа задания функции одной и нескольких переменных,

– распознавание вида неопределенности.

При чтении лекции используется объяснительно-иллюстративный метод, позволяющий ввести студентов в понятийно-категориальный аппарат данного раздела математики.

Ориентация на развитие компетенций:

ОК-5 – способность к самоорганизации и самообразованию;

ПК-1 – способность к анализу и синтезу;

ПК – 8: способность использовать информационные средства и технологии при решении задач, возникающих в ходе профессиональной деятельности;

ОПК-4 – готовность сочетать теорию и практику для решения инженерных задач.

2.1.1. Переменная величина

Понятие «величина» – основное понятие, с которым мы встречаемся в любой естественнонаучной или технической области знания. Под величиной понимают все то, что может быть измерено и выражено числом (числами). Например, длина, площадь, объем, вес, температура, скорость, сила и т. п.

Обычно, среди совместно рассматриваемых величин некоторые изменяются, другие же остаются постоянными.

Переменной величиной называют величину, которая принимает различные численные значения; величина, которая сохраняет одно и тоже численное значение, называется постоянной.

Переменная величина считается заданной, если задана совокупность её значений. Совокупность значений переменной величины называется областью изменения переменной величины.

Переменные величины делятся на два класса: непрерывные и дискретные.

Переменная величина называется непрерывной, если областью её изменения является некоторый интервал. Переменная величина называется дискретной, если областью её изменения является множество изолированных точек. Например, скорость ветра – непрерывная величина, число студентов в аудиториях – дискретная величина.

Переменная величина называется упорядоченной, если из двух значений переменной величины можно указать предыдущую и последующую.

Если переменная величина в области изменения убывает или возрастает, то она называется монотонной.

Если значения переменной величины таковы, что число будет больше (меньше) любого значения переменной величины, то говорят, что переменная величина ограниченна сверху (снизу). Переменная величина называется ограниченной, если она ограничена сверху и снизу.

2.1.2. Функция одной и нескольких переменных

Чаще всего изменению одной переменной величины сопутствует изменение другой, более того, изменение одной является причиной изменения другой. В некоторых случаях изменение одной переменной величины может быть продиктовано изменением двух, трех и более величин.

Примеры.

1. Площадь квадрата изменяется в зависимости от изменения длины его стороны .

2. Работа, совершаемая на некотором прямолинейном участке пути под действием некоторой силы, изменяется в зависимости от изменения длины участка и величины силы воздействия .

3. Периметр треугольника изменяется в зависимости от длин его сторон и .

4. Сила взаимодействия двух электрических зарядов по закону Кулона изменяется в зависимости от изменения величин зарядов и , значения диэлектрической проницаемости и расстояния между зарядами .

Таким образом, всякий процесс характеризуется взаимоизменяемостью нескольких переменных величин. Такое представление приводит к важнейшему в математике понятию функциональной зависимости, т.е. связи между переменными величинами. Важнейшей задачей математического анализа является всестороннее изучение функциональных зависимостей.

Пусть даны и – переменные величины, и – области изменения этих величин.

О пределение. Если каждому значению величины по некоторому закону соответствует единственное значение величины , то говорят, что задана функция , или что величины и связаны между собой функциональной зависимостью (см. рис. 2.1.1).

При этом, – аргумент функции (независимая переменная), – значение функции (зависимая переменная), – закон соответствия, – функция одной независимой переменной.

Множество называется областью определения функции и обозначается . Множество называется областью значений функции и обозначается .

Иногда функциональную зависимость от пишут в виде , не вводя новой буквы для обозначения зависимости.

Исходя из определения, областью определения функции , является множество значений , при которых функция имеет смысл.

Для функции одной переменной областью определения является интервал координатной оси или вся координатная ось.

Пример. Для функции найти и изобразить её.

Р ешение: .

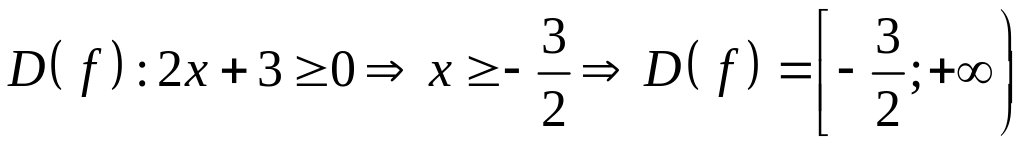Ответ: .

Пусть даны и – переменные величины, – область изменения пар чисел , а – область изменения .

Определение. Если каждой паре чисел по некоторому закону соответствует единственное значение величины , то говорят, что задана функция (см. рис. 2.1.2).

П ри этом – аргументы функции (независимые переменные), – значение функции (зависимая переменная), – закон соответствия, – функция двух независимых переменных, – область определения функции, – область значений функции.

Д ля функции двух переменных область определения является часть координатной плоскости или вся координатная плоскость.

Пример. Для функции найти и изобразить ее.

Решение: . Значит, областью определения является часть плоскости , координаты точек которой удовлетворяют неравенству , т.е. полуплоскость, расположенная выше прямой . Так как точки прямой не удовлетворяют неравенству , то прямая изображается пунктирной линией (см. рис.2.1.3).

Ответ: .

Определение. Если каждой совокупности переменных величин по некоторому закону соответствует единственное значение , то говорят, что задана функция – функция независимых переменных.

Для функции трех переменных область определения функции геометрически представляется в виде части трехмерного пространства.

Для функции переменных, при , область определения невозможно представить геометрически.