Системы со многими степенями свободы свободные колебания системы со многими степенями свободы

Для упругой системы с «n» степенями свободы существует «n» возможных форм колебаний и соответственно «n» частот колебаний. Совокупность частот данной системы составляет ее спектр частот. Наибольшую опасность в смысле возможности возникновения резонанса с вибрационной нагрузкой, представляет наименьшая частота. Ее иногда наз. частотой основного тона колебаний. Следующий по порядку тон колебаний наз. первым обертоном.

Для примера рассмотрим простую балку с 3 точечными массами m₁, m₂ и m₃. Такая балка имеет 3 ст.св. и характеризуется 3-я частотами свободных колебаний: ₁, ₂, ₃ (рис.20).

Рис.20

Для определения этих частотой составим выражения перемещений точек приложения сосредоточенных масс под действием сил инерции

(26)

Перемещения ₁₁, ₂₂, ₃₃, ₁₂=₂₁, ₁₃=₃₁ и ₂₃=₃₂ вычисляются, как обычно, способом Мора или Верещагина от единичных сил, приложенных в местах действия сил инерции, т.е. в сечениях, где находятся массы.

Система диф. уравнений (26) имеет следующие решения:

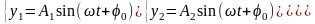(27)

А₁, А₂ и А₃ – амплитуды колебаний соответствующих масс; ₀ – начальная фаза колебаний.

Вторые производные (ускорение) по времени выражаются так:

(28)

Подставив (28), (27) в (26) и сократив на ²sin(t+) получим

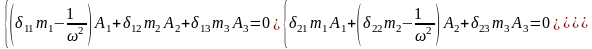(29)

Тривиальное решение этой системы уравнений А₁=А₂=А₃=0 соответствует случаю, когда система находится в покое.

А для того, чтобы амплитуды были отличны от нуля, определитель, составленный из коэффициентов при амплитудах должен быть равен нулю т.е.

(30)

Раскрыв этот определитель, получим одно уравнение третьей степени относительно , которое дает три положительных значений частот .

В общем виде, для системы с «n» степенями свободы этот определитель запишется так:

(если обозначим =)

(31)

Это уравнение частот или вековое уравнение (впервые эти уравнения были получены в астрономии и периоды движения планет характеризовались квадратами величин измеряемых в веках).

В практических расчетах наиболее часто встречаются системы с двумя ст.свободы, для которых уравнение (6.6) можно записать в виде:

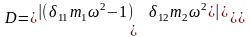
Раскрыв определитель и решая уравнения получим:

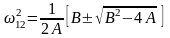(32)

где ; .

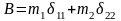Главные формы колебания

Если направления перемещений у₁, у₂…у_n выбраны так, что побочные перемещение _ik обращаются в нуле, то система диферен. уравнений (26) и соответствующие уравнения частот распадаются на отдельные уравнения, содержащие только главные перемещения.

В этом случае перемещения у₁, у₂…у_n. называются главными координатами, а соответствующие формы колебаний – главными формами колебаний. При этом подразумевается такая измененная форма, соответствующая частота колебания системы, для которой sin(_it+_i)=1. Главные формы колебаний обособлены друг от друга и каждая из них происходит с определенной частотой, которая выражается формулой

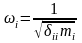(33)