Вынужденные колебания системы с одной степенью свободы при действии гармонической нагрузки

Вынужденными называются колебания системы, на массу которой кроме восстанавливающей силы F, силы инерции J и силы сопротивления среды R действует еще и возмущающая сила, изменяющаяся во времени Р(t).

Для расчета пром. сооружений на практике часто возмущающую силу принимают сосредоточенную, изменяющуюся по гармоническому закону Р(t)=Рsint.

Где Р – амплитуда возмущающей силы

 - круговая частота возмущающей силы.

Так, по гармоническому законам изменяются вертикальная (Р_у) и горизонтальная (Р_х) составляющие центробежной силы, возникающей при наличии неуравновешенной массы m равномерно вращающейся части машины (рис.13)

Рис.13

Рассмотрим вынужденные колебания той же консольной балки без учета сил сопротивления (рис.14)

Тогда вместо однородного диф. уравнения (1) получим неоднородное, т.е. с правой частью

(9)

Рис.14

(10)

Полное решение уравнения (10) будет состоять из общего решения соответствующего однородного уравнения (2) и частного решения уравнение (10):

Подставляя в (10) получим выражение постоянной интегрирования b:

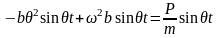
Отсюда

Тогда

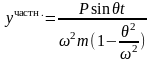
Полное решение уравнения (10) получим в виде:

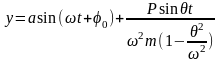(11)

Первый член этого уравнения выражает свободные колебания, а второй - вынужденные с частотой .

Анализ колебаний показывает, что со временем, в результате сопротивления среды, свободные колебания, затухают и система колеблется под воздействием возмущающей нагрузки с частотой .

Тогда

здесь .

Величину обозначим через , т.е.

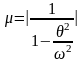(12)

Тогда .

 - динамический коэффициент гармонической нагрузки, показывающий, во сколько раз ее динамическое действие превышает статическое действие ее амплитуды (Р)

у_ст=у_дин.

т.е. динам. коэффициент – это отношение динамического прогиба к статическому.

Как видно из выражения (12),  зависит от отношение . С увеличением этого отношения,  тоже увеличивается, и при , = (бесконечно большое число).

Явление, при котором  наз. резонансом. Это явление очень опасно для сооружений, т.к. амплитуда вынужденных колебаний сильно возрастает.

Рис.15

Как видно из графика (рис.15), при <, 1 (линия I), т.е. сооружение совершает вынужденные колебания в одной фазе с возмущающей силой.

При >, <1 (линия II) – сооружение и возмущающая нагрузка колеблются в противоположных фазах: возмущающая нагрузка направлена вниз, а масса m движется вверх и наоборот.

Для исключения явления резонанса при расчете сооружений на динамическую нагрузку, принимают

0,8

Вынужденные колебания системы с одной степенью свободы с учетом сил сопротивления среды

Если же в рассмотренном случае учесть и силу сопротивления (R), то уравнения динамического равновесия будет:

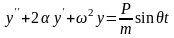(13)

Полное решение этого дифференциальное уравнение будет состоять из общего и частного решений. Первое получим, приравняв правую часть уравнения нулю. Частное решение ищем в виде:

(14)

а и b – постоянные величины. Для их определяется, возьмем вторые и первые производные выражения (14) и подставим в уравнение (13), получим:

или

Отсюда, для определение а и b получаем два уравнения:

Решая эти уравнения совместно, получаем:

где

Таким образом, у^частн. получаем в виде:

Обозначим

Тогда

А полное решение уравнения (13) будет:

(15)

Первая часть этого выражения характеризует свободные колебания с учетом затухания, и с течением времени затухают. Вторая же часть - вынужденные колебания. С течением времени свободные колебания затухают и остаются только лишь вынужденные колебания с частотой . Уравнение такого колебание:

 - сдвиг фазы вынужденных колебаний по отношению к возмущающей силе

• динамический коэффициент гармонической нагрузки с учетом затухания.

При совпадении частот (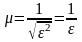) (в отличие от вынужденных колебаний без учета сопротивления среды, когда при  ).

График зависимости  от при затухании (при различных ) (рис.16).

Рис.16

При  в сопротивляемой среде резонанса не возникает. Но  резко увеличивается и сооружение работает в зоне резонанса.

Максимальное значение _дин. достигает при .

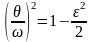Тогда

Т.о., при резонансе амплитуда вынужденных колебаний обратно пропорциональна логарифмическому декременту  .

Пример: Определить динамический коэффициент вынужденных колебании балки (массы m) (рис.17)

Рис.17

Дано: стальная двутавровая балка (Е=2,110⁶, J= 8950 см⁴, W=597 см³). Груз Q=mg=3T=3000 кГс; =42 сек^-1. Р=0,8=800 кГс (>100кГс). Поэтому из табл. =0,025.

Частота свободных колебаний для систем с 1 степенью свободы:

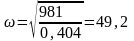сек^-1

Если не учитывать сопротивление среды

Следовательно, учет сопр. среды (затухания) при отсутствии резонанса почти не изменил величину дин. коэф. при резонансе () (большой).