Устойчивость плоских рам

Постановка задачи и схема решения при расчете на устойчивость первого рода:

Допущения:

1) Рассматривается только узловая нагрузка, не вызывающая поперечного изгиба стержней рамы.

2) Стержни считаются нерастяжимыми и несжимаемыми.

3) Изменением расстояния между концами стержня пренебрегаем.

Рис.37

4) При работе учитываются нормальные силы, возникающие до потери устойчивости. Рассмотрим раму

Задачей расчета является определение критической нагрузки.

Т.к. изогнутое состояние есть состояние равновесия, расчет может быть произведен любым из методов, применяемых к расчету равновесных систем, в том числе методом сил или методом перемещений. Основные системы (рис.38).

Рис.38

При отсутствии моментов от нагрузки в основной системе все свободные члены канонических уравнений равны нулю и система уравнений приобретает вид:

для метода сил:

для метода перемещений:

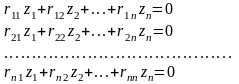
В этих уравнениях _ik и r_ik соответственно перемещения и реакции по направлению i от единичных лишних неизвестных при наличии продольных сил в стержнях. Т.о. в _bk и r_ik входит параметр нагрузки Р.

В изогнутом равновесном состоянии X_i0 и z_i0 поэтому:

или

Из этих определителей и определяется критический параметр нагрузки.

В расчетах на устойчивость для большинства типов рам метод перемещений требует более простых и менее трудоемких вычислений, чем метод сил.

Дифференциальное уравнение изгиба сжатоизогнутого стержня и его интеграл

Рис.39

Пусть первоначально прямолинейный стержень АВ под действием сосредоточенных сил Р_i равномерной нагрузки q моментов и поперечных сил по концам М_А, Q_A, M_B, Q_B и постоянной продольной силы N изогнулся и переместился (рис.39)

Изгибающий момент в произвольном сечении:

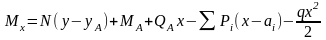
Дифференциальное уравнение изгиба

Отсюда

(67)

Обозначим , тогда получаем полное решение дифференциальное уравнение (67):

(68)

с₁ и с₂ определяем из граничных условий:

при х=0; у=у_А; с₁

при х=0 .

Подставив в (68), после небольших преобразований, получим окончательную формулу для прогиба и, путем последовательного дифференцирования – формулы для углов поворота, моментов и поперечных сил в произвольном сечении сжатоизогнутого стержня:

(69)

представляют собой влияние пролетной нагрузки на соответствующую функцию.

Пример: Рассмотрим балку, защемленную двумя концами, в которой, при помощи постоянной продольной силы N произошел поворот левой заделки на угол, равный единице (рис.40):

Рис.40

Из четырех начальных параметров два известны:_А=1, у_А=0.

Остальные два определяются из условий: у_В=0, :_В=0 (а)

Подставляя значение х=l и условия (а) в первые два из уравнение (69), получим М_А и Q_A:

Подставляя М_А и Q_A в (3) и (4) уравнения (69), получим

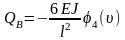
Так же можно рассматривать и другие случаи сжатоизогнутых стержней.

Реакции сжатоизогнутых стержней от единичных перемещений.

Расчет рам на устойчивость методом сил

Как было указано выше, для получения однородной системы канонических уравнений основная система должна быть выбрана так, чтобы в ней не возникло изгибающих моментов от заданной нагрузки. Кроме того, при вычислении _ik учитывается влияние продольных сил, которые имели места до потери устойчивости, на изгибные деформации при потере устойчивости (как и в методе перемещений).

Наиболее просто интеграл Мора вычисляется в тех основных системах, в которых сжатые стержни представляемой собой простые балки с шарнирно опертыми несмещающимися концами или балки, защемленными одним концом.

Рис.41

Лишними неизвестными при расчете на устойчивость по методу сил является те малые усилия в отброшенных связях, которые появляются при потере устойчивости. В результате расчета эти силы остаются неопределенными.

Выведем окончательные формулы для требуемых в случае простейших основных систем интегралов Мора.

а) Стержень, защемленный одним концом (рис.41).

Рассмотрим стержень, защемленный одним концом и нагруженный на другом конце произвольной поперечной силой Q_A=е, произвольным моментов М_А=с и продольной силой N. Эпюра изгибающего момента будет криволинейна, причем в заделке

где d – момент от поперечного нагрузка

Момент в произвольном сечении х получим, воспользовавшись формулами (69)

При х=l =0 

Подставляя полученное значение _А в третье уравнение (69), после преобразований, находим

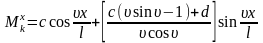
В прямолинейной эпюре момент в произвольном сечение

таким образом, проинтегрировав, получаем:

(70)

где

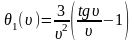
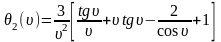
Величина  для различных значений  даются в таблице. Ординаты эпюр берутся из эпюр от поперечной нагрузки. Влияние продольной силы заключено в коэффициенте .

б) Стержень шарнирно опертый (рис.42)

Рис.42

Подставив у_В=0 в (69), получим

Таким образом,

(71)

где

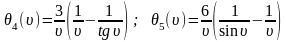
Пример: Определим Р_кр (рис.43а).

n_cm=2. Выбираем основную систему (рис.43 б).

Строим эпюры изгибающих моментов от единичных значений Х₁=1 и Х₂=1, учитывая действующую продольную силу Р (рис.43 в, г).

Рис.43

Уравнение устойчивости:

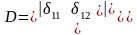
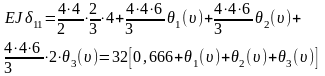
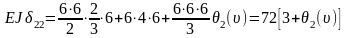
После подстановки в уравнение устойчивости

Подбором находим то значение , при котором это уравнение удовлетворяется.

При =3,12 ₁()=-0,31; ₂()=0,902; ₃()=-0,612.

а коэффициент свободной длины сжатой стойки