AZƏRBAYCAN RESPUBLİKASI TƏHSİL NAZİRLİYİ

AZƏRBAYCAN MEMARLIQ VƏ İNŞAAT UNİVERSİTETİ

NƏZƏRİ MEXANİKA VƏ İNŞAAT MEXANİKASI kafedrası

Fənnin adı: Строительная механика–2 расчет методом перемещений

Как и метод сил, метод перемещений является одним из важнейших методов расчета статически неопределимых систем. В качестве неизвестных (как видно из названия метода) в этом методе принимают упругие перемещения узлов системы: углы поворота узлов и их линейные перемещения (рис.42).

Рис. 42

Общее число неизвестных метода перемещений n_кин, называемое степенью кинематической неопределимости системы, определяют как сумму неизвестных углов поворота n_у и неизвестных линейных перемещений узлов n_л:

n_кин= n_у + n_л (33)

Число n_у равно числу «жестких» узлов. Для определения n_л необходимо условно во все «жесткие» узлы и опоры заданной системы ввести шарниры.

Степени свободы полученной шарнирной системы и будет равно число n_л; n_л=n_св.

Для рассмотренной на рис.42 рамы n_к=n_у + n_л, n_у=2;

Введем во все «жесткие» узлы и опоры заданной системы шарниры.

n_св=3D – 2Ш – С_опор

n_св=34  23 – 5 = 1

n_л= n_св=1

n_к=2 + 1 =3.

Рис. 42

После определения числа неизвестных образуют основную систему метода перемещений путем наложения на узлы заданной системы связей, препятствующих их перемещениям. В соответствии с принятыми неизвестными эти связи бывают двух типов: связи, препятствующие повороту узлов (защемления) и связи, препятствующие линейным перемещениям узлов (опорные стержни). Отметим, что вводимые в основную систему защемляющие связи отличаются от обычной жесткой заделки тем, что оказывают препятствие только повороту узла и не лишают его линейной подвижности.

Общее число вводимых в основную систему связей равно, естественно, числу неизвестных (рис.43), которые будем обозначать Z_i.

Рис. 43

Полученная основная система статически неопределимая, но кинематически определимая система.

Отметим, что в отличие от метода сил, в методе перемещений можно показать только один вариант основной системы.

Для определения основных неизвестных Z_i канонические уравнения метода перемещений записываются в виде:

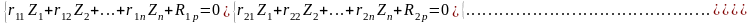(34)

Каждое из этих уравнений выражает условие, что суммарная реакция каждой наложенной на заданную систему связи равна нулю, т.к. в заданной системе эти связи отсутствуют.

В защемленных дополнительных связях основной системы возникают реактивные моменты, а в дополнительных стержнях – силы.

Для рассмотренной на рис.42 рамы канонические уравнения будут:

В левой части первого уравнения стоит суммарная реакция (момент) первой дополнительной связи (защемления) в заданной системе, и т.д.

Входящие в канонические уравнения коэффициенты при неизвестных r_ik представляют собой реактивные усилия (моменты или силы), возникающие в связи i от единичного перемещения Z_k связи к. Свободные члены этих уравнений R_ip – реактивные усилия в связи i от внешней нагрузки.

Коэффициенты с одинаковыми индексами r₁₁, r₂₂… называемые главными всегда положительны и не равны нулю. Побочные коэффициенты r₁₂, r₃₂, …, как и в методе сил r_ik= r_ki.

Для определения коэффициентов и свободных членов канонических уравнений необходимо предварительно построить эпюры изгибающих моментов в основной системе от единичных неизвестных перемещений (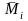 ) и от внешней нагрузки (М_р).

Так как основная система метода перемещений представляет собой совокупность независимых элементов – однопролетных статически неопределимых балок, двух типов (с двумя защемленными концами и с одним защемленным другим шарнирным концами), построения указанных эпюр сводится к определению усилий в однопролетных балках от перемещений их концов и от нагрузки. Эти усилия и эпюры моментов, вычисленные для наиболее важных случаев, приведены в таблице 1.

После построения эпюр изгибающих моментов, коэффициенты и свободные члены канонических уравнений вычисляются из уравнений равновесия. Например, коэффициенты и свободные члены, представляющие реактивные моменты во введенных защемлениях, определяются из условий равновесия вырезанных из основной системы узлов в виде М_i=0.

Коэффициенты при неизвестных и свободные члены уравнений, представляющие реактивные усилия во введенных стержневых связях, могут быть определены из условий равновесия некоторой отсеченной части основной системы, содержащей эти связи (Х_i=0 или У_i=0).

После определения из канонических уравнений основных неизвестных Z₁,…,Z_n эпюра изгибающих моментов для заданной системы строятся по формуле:

(35)

а эпюры поперечных и продольных сил (Q и N) так же, как в методе сил.

Проверкой правильности полученных эпюр является статическая проверка условий равновесия вырезанных узлов и заданной рамы как в целом, так и отдельных ее частей.