3 Рабочая программа раздела курса «Кинематика точки»

Кинематика. Предмет кинематики. Пространство и время в классической механике. Относительность механического движения. Системы отсчета. Задачи кинематики точки.

Литература: [1, 143-144; 5, 142-143].

Вопросы для самопроверки:

1.Что изучает кинематика?

2. Какое движение называется механическим. Приведите примеры?

3.Сформулируйте основные задачи кинематики точки.

Кинематика точки. Векторный способ задания движения точки. Траектория точки. Скорость точки как производная ее радиуса-вектора по времени. Ускорение точки как производная ее вектора скорости по времени. Координатный способ задания движения точки (в прямоугольных декартовых координатах). Определение траектории точки. Определение скорости и ускорения точки по их проекциям на координатные оси. Естественный способ задания движения точки. Естественный трехгранник. Алгебраическая величина скорости точки. Определение ускорения точки по его проекциям на оси естественного трехгранника; касательное и нормальное ускорения точки. Равномерное и равнопеременное криволинейные движения точки; законы этих движений.

Литература: [1, 144-183; 5, 143-183].

Вопросы для самопроверки:

1.Перечислите способы задания движения точки.

2.Как задать движение точки векторным способом?

3.Как задать движение точки координатным способом?

4.При каких условиях можно задать движение точки естественным способом? Какие оси называются естественными?

5.Как определить модули и направления скорости и ускорения точки при различных способах задания движения?

4 Кинематика точки (задача к1)

4.1 Условие задачи К1

По заданным уравнениям движения точки и , заданным в таблице 6, найти и построить на рисунке в масштабе:

– траекторию движения точки;

– положение точки М_о в начальный момент времени = 0;

– положение точки М₁ в заданный момент времени , с;

– скорость и ускорение точек М_о и М₁ в начальный и заданный моменты времени;

– касательное и нормальное ускорения, радиус кривизны траектории для точек М_о и М₁.

2. Пример решения задачи К1

Движение точки задано координатным способом уравнениями:

x = 2 sin ( t) + 3; y = 4 cos ( t). (4.1)

Для момента времени t = 1c определить кинематические параметры ее движения в соответствии с условием задачи К1.

Решение

Уравнения движения являются одновременно уравнениями траектории точки в параметрической форме. Для получения уравнения траектории из уравнений движения необходимо исключить параметр t:

sin ( t ) = ; cos ( t ) = .

Если обе части каждого равенства возвести в квадрат и сложить левые и правые части, то получим уравнение эллипса:

+ = 1. (4.2)

Полуоси эллипса: горизонтальная = 2 м, вертикальная b = 4 м, координаты его центра = 3 м; = 0.

Траекторию точки строим в масштабе на рисунке (рис. 73).

Для определения положения точки на траектории в уравнения ее координат подставляем соответствующее время.

В начальный момент времени при t = 0 из уравнений (4.1) получим:

= 3 м , = 4 м.

В заданный момент времени при = 1 c из этих уравнений найдем:

= 2 sin + 3 = 4,4 м ; = 4 cos = 2,8 м.

Положения точек М_о и М₁ показываем на траектории (рис. 73).

Скорость и ускорение точки найдем по их проекциям на оси координат: ; ; (4.3)

; . (4.4)

Тогда в начальный момент времени при t = 0 получим:

м/с; ;

= 1,57 м/с;

; м/ ;

.

В заданный момент времени при :

; ;

;

; ;

.

Выбираем масштаб скорости и ускорения и строим векторы скорости и ускорения и их проекции для точек М_о и М₁ (рис. 73). Величину выбранного масштаба необходимо указать на рисунке.

Определим касательное, нормальное ускорения точки и радиус кривизны ее траектории.

При движении точки по криволинейной траектории ускорение точки можно выразить через проекции на естественные оси: касательную и нормаль: ,

где – касательное ускорение точки: ; (4.5)

– нормальное ускорение: ; (4.6)

– радиус кривизны траектории.

Нормальное ускорение можно вычислить, зная полное ускорение точки и его касательную составляющую: . (4.7)

Подставляем в формулы (4.50), (4.51), (4.52) значения величин, найденных для соответствующих моментов времени. В начальный момент времени при :

; ;

В заданный момент времени при :

;

Рисунок 73 – Схема к решению задачи К1

Таблица 1 – Исходные данные к задаче К1

Номер варианта	Уравнения движения точки, м		Заданный момент времени, с
	x =	y =
1	2	3	4
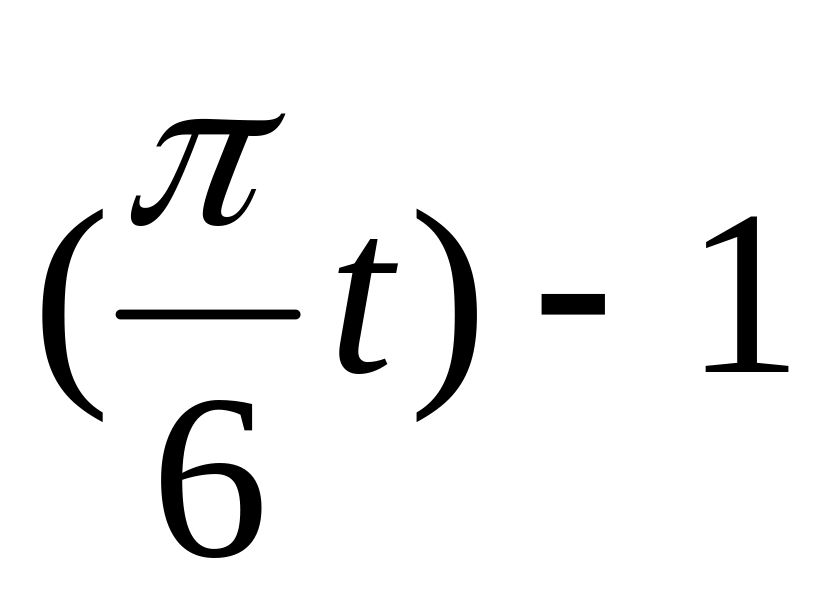
1	х = 4cos +3	у = 5sin	2
2	х = 3sin	у = 4cos	1
3	х = 6sin	у = 2cos(	1
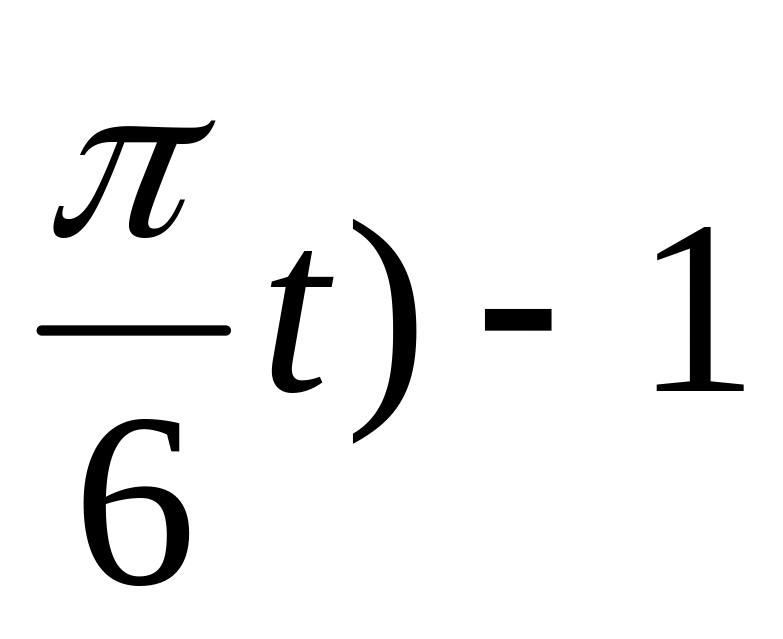
4	х = 4cos (	у = 2sin	1
5	х = 4cos	у = 3sin(	2
6	х = 4sin(	у = 2cos t)	2

Продолжение таблицы 1

1	2		3		4
7	х = 5-2cos		у = 3sin( -1		1
8	х = sin(		у = 2cos -3		1
9	х = 3cos		у = 2sin		1
10	х = 2sin		у = 4cos(		2
11	х = 4sin(		у = 5cos		1
12	х = 5sin(		у = 2cos(		1
13	х = 3sin(		у = 6cos		1
14	х = 3cos(		у = 2 – 4sin		2
15	х = sin(		у = 2cos		1
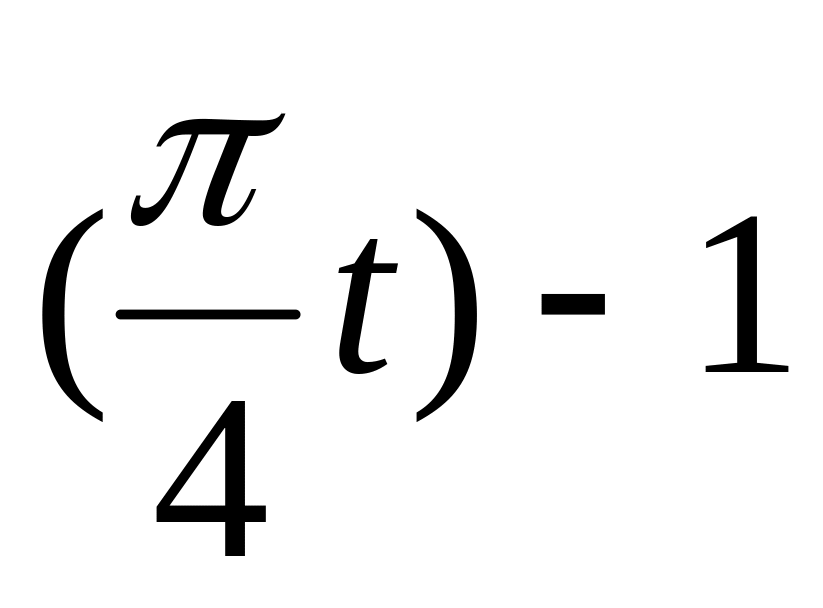
16		х = sin		у = 4cos( )+2	1
17		х = 2cos(		у = 5sin(	1
18		х = 5cos(		у = 3sin	1
19		х = 2sin		у = 4cos	1
20		х = 4cos		у = 6sin	1
21		х = 2cos		у = 5sin	1
22		х = 6sin(		у = 4cos	1
23		х = 5cos(		у = 7sin	1
24		х = 3sin(		у = 5cos	1
25		х = 4+2sin		у = 5cos	1
26		х = 7sin		у = 4cos	1
27		х = 3sin( )+3		у = 2cos( ) – 1	2

Продолжение таблицы 1

28	х = -2cos(	у = 4sin	1
29	х = 2sin +3	у = 4cos - 2	1
30	х = 2cos - 2	у = 4sin + 3	1

В выбранном масштабе ускорений показываем проекции ускорения точек М_о и М₁ на естественные оси координат (рис. 73), что позволяет осуществить проверку решения.

На графике необходимо соблюсти условия:

.