
- •Отличие наномира от мира классической физики и от мира квантовой механики
- •Подвижность электронов
- •Межатомные связи в твердых телах Методы валентности, молекулярных орбиталей.
- •3. Основные характеристики полевого транзистора с управляющим р-п переходом Основные параметры полевых транзисторов с управляющим р-n-переходом
- •7. Автоэмиссионная электроника
- •26. Модель обратного рассеяния в электронной литографии
- •41. Вольтовый контраст в рэм
- •51. Принцип работы сканирующего туннельного микроскопа
- •54. Конфокальная микроскопия
Межатомные связи в твердых телах Методы валентности, молекулярных орбиталей.
Ионная связь – присуща химическим соединениям, образованным элементами с резко различающейся валентностью. Так металлы, имея 1 или 2 электрона на внешней орбите, которые не прочно связаны с ядром, вступая в реакцию с неметаллами, металлы отдают электроны и превращаются в ионы. Неметаллы принимают эти электроны, превращаясь в отрицательные ионы => ионная связь обеспечивает электро – статическое притяжение. Ионная связь жесткая и направленная => все прочные, твердые, но очень хрупкие (низкая пластичность). Ионная связь характерна для окислов различных элементов. Ковалентная связь – устанавливается в результате образования устойчивых соединений, путем обобществления электронов группой атомов. Обобществление электронов зависит от валентности элемента. Ковалентная связь возникает между атомами соседей, которые обобществляют один из электронов соседа. Ковалентная связь характерна для кристаллических тел. Ковалентная связь – жесткая, направленная => прочная. Она характерна для пластмасс. Металлическая связь обусловлена строением атома, на внешней орбите у металла 1-2 электрона, они слабо связаны с ядром. Для металла характерны кристаллические решетки с плотным расположением атомов => внешние оболочки соприкасаются и пересекаются. Все валентные электроны обобществляются (общие в пределах твердого тела) и образуют электронный газ. Возникают пары атомов превращающихся в разнозаряженных атомов, которые связаны силами электростатического напряжения. Металлическая связь – гибкая, нежесткая. Свойства металлов: высокая прочность, пластичность, электропроводность, теплопроводность. Металлическая связь характерна всем металлам и их сплавам . Метод вал.св. -метод приближенного решения электронного ур-ния Шрёдингера для многоэлектронных молекулярных систем. Осн. физ. идея валентных связей метода состоит в том, что волновая ф-ция молекулы выражается через волновые ф-ции составляющих ее атомов. Образование хим. связи рассматривается как результат спаривания спинов своб. электронов атомов. ММО- В основе метода лежит представление о том, что каждый электрон молекулы описывается своей волновой функцией — молекулярной орбиталью (МО). Вследствие невозможности точно решить Шрёдингера уравнение для систем с двумя и более электронами, способ получения выражения для МО неоднозначен.
Зонная теория твердого тела. Зонная теория твердого тела - приближенная теория движения электронов в периодическом поле кристаллической решетки, согласно которой:
Все физические свойства твердых тел определяются внешними (валентными) электронами, которые перемещаются по всему объему кристалла от одного атома к другому и возможные уровни энергии которых образуют энергетические зоны.


Молекулярные решетки. Молекулярными называют такие кристаллические решетки, в узлах которых расположены молекулы. Химические связи в этих молекулах могут быть также, как полярными (HCl, H20), так и неполярными (N2, O3). И хотя атомы внутри молекукл связаны очень крепкими ковалентными связями, между самими молекулами действует слабые силы межмолекулярного притяжения. Именно поэтому вещества с молекулярными кристаллическими решетками характеризуются малой твердостью, низкой температурой плавления, летучестью.
Примерами таких веществ могут послужить твердая вода – лед, твердый оксид углерода (IV) – «сухой лед», твердые хлороводород и сероводород, твердые простые вещества, образованные одно – (благородные газы), двух – (H2, O2, CL2, N2, I2), трех – (O3), четырех – (P4), восьмиатомными (S8) молекулами. Подавляющее большинство твердых органических соединений обладают молекулярными кристаллическими решетками (нафталин, глюкоза, сахар).
Ионные кристаллы ИОННЫЕ КРИСТАЛЛЫ, кристаллич. в-ва, в к-рых сцепление между частицами обусловлено преим. ионными связями. Поскольку между ионными и полярными ковалентными связями существует непрерывный переход, нет резкой границы между ионными кристаллами и ковалентными кристаллами. К ионным относят кристаллы, в к-рых связи между атомами наиб. полярны; в осн. это соли щелочных и щел.-зем. металлов. Ионные кристаллы отличаются высокими т-рами плавления, обычно значит. шириной запрещенной зоны, обладают ионной проводимостью при высоких т-рах и рядом специфич. оптич. св-в (напр., прозрачностью в ближней области ИК спектра). Они м. б. построены как из одноатомных, так и из многоатомных ионов. Пример ионных кристаллов первого типа - кристаллы галогенидов щелочных и щел.-зем. металлов; анионы располагаются по закону плотнейшей шаровой упаковки или плотной шаровой кладки (см. Плотная упаковка), катионы занимают соответствующие пустоты. Наиб. характерные структуры такого типа - NaCl, CsCl, CaF2. Ионные кристаллы второго типа построены из одноатомных катионов тех же металлов и конечных или бесконечных анионных фрагментов. Конечные анионы (кислотные остатки) - NO3-, SO42-, СО32- и др. Кислотные остатки могут соединяться в бесконечные цепи, слои или образовывать трехмерный каркас, в полостях к-рого располагаются катионы, как, напр., в кристаллич. структурах силикатов. Для ионных кристаллов можно рассчитать энергию кристаллич. структуры U (см. табл.), приближенно равную энтальпии сублимации; результаты хорошо согласуются с эксперим. данными. Согласно ур-нию Борна-Майера, для кристалла, состоящего из формально однозарядных ионов:
U = -A/R + Ве-R/r - C/R6 - D/R8 + E0
(R - кратчайшее межионное расстояние, А - константа Маделунга, зависящая от геометрии структуры, В и r - параметры, описывающие отталкивание между частицами, C/R6 и D/R8 характеризуют соотв. диполь-дипольное и диполь-квадрупольное взаимод. ионов, E0 - энергия нулевых колебаний, е - заряд электрона). С укрупнением катиона возрастает вклад диполь-дипольных взаимодействий.
Ковалентные решетки. Ковалентные решетки состоят из атомов. Ковалентная связь возникает между атомами, обладающими неспаренными электронами. Например, атом углерода может образовать четыре одинарные кова-лентные связи, направленные к четырем вершинам правильного тетраэдра, в центре которого располагается атом углерода. ковалентные решетки состоят из атомов. Ковалентная связь возникает между атомами, обладающими неспаренными электронами. Следовательно, с этим центральным атомом могут быть связаны четыре других атома углерода. Каждый из них обладает еще тремя неспаренными электронами, которые могут образовывать связь с тремя атомами углерода.
Металлические решетки. Металлическая связь — химическая связь между атомами в металлическом кристалле, возникающая за счёт обобществления их валентных электронов. В узлах кристаллической решётки расположены положительные ионы металла. Между ними беспорядочно, подобно молекулам газа, движутся электроны проводимости, происходящие из атомов металлов при образовании ионов. Эти электроны играют роль «цемента», удерживая вместе положительные ионы; в противном случае решётка распалась бы под действием сил отталкивания между ионами. Вместе с тем и электроны удерживаются ионами в пределах кристаллической решётки и не могут её покинуть. Силы связи не локализованы и не направлены. В металлах в большинстве случаев проявляются высокие координационные числа (например, 12 или 8). В металлах валентные электроны удерживаются атомами крайне слабо и способны мигрировать. Атомы, оставшиеся без внешних электронов, приобретают положительный заряд. Они образуют металлическую кристаллическую решётку.
Совокупность обобществлённых валентных электронов (электронный газ), заряженных отрицательно, удерживает положительные ионы металла в определённых точках пространства - узлах кристаллической решётки, например, металла серебро.
Внешние электроны могут свободно и хаотично перемещаться, поэтому металлы характеризуются высокой электропроводностью (особенно золото, серебро, медь, алюминий).
Фононы Фононы. квазичастица, представляет собой квант колебательного движения атомов кристалла. Акустический фонон характеризуется при малых волновых векторах линейным законом дисперсии и параллельным смещением всех атомов в элементарной ячейке. Оптические фононы существуют только в кристаллах, элементарная ячейка которых содержит два и более атомов. Эти фононы характеризуются при малых волновых векторах такими колебаниями атомов, при которых центр тяжести элементарной ячейки остается неподвижным. Энергия оптических фононов обычно достаточно велика (порядка 500 см−1) и слабо зависит от волнового вектора.
Магноны Магно́н — квазичастица, соответствующая элементарному возбуждению системы взаимодействующих спинов. В кристаллах с несколькими магнитными подрешётками (например, антиферромагнетиках) могут существовать несколько сортов магнонов, имеющих различные энергетические спектры. Магноны подчиняются статистике Бозе — Эйнштейна. Магноны взаимодействуют друг с другом и с другими квазичастицами. Существование магнонов подтверждается экспериментами по рассеянию нейтронов, электронов и света, сопровождающемуся рождением или уничтожением магнона

Экситоны Экситоны— водородоподобная квазичастица, представляющая собой электронное возбуждение в диэлектрике или полупроводнике, мигрирующее по кристаллу и не связанное с переносом электрического заряда и массы. состоит из электрона и дырки. Экситон можно считать элементарной квазичастицей в тех явлениях, в которых он выступает как целое образование, не подвергающееся воздействиям, способным его разрушить.Экситон может быть представлен в виде связанного состояния электрона проводимости и дырки, расположенных или в одном узле кристаллической или на расстояниях, значительно больше междуатомных.
Поляроны.


Понятие фрактала Фрактал.— сложная геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. Ф — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба. Ф — самоподобное множество нецелой размерности. Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — математическое множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей). В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев. Самоподобные фигуры, повторяющиеся конечное число раз, называются предфракталами.
Примеры фрактальных структур «У попа была собака..»
Снежинка Коха

Алгебраические фракталы.
Чтобы проиллюстрировать алгебраические фракталы обратимся к классике - множеству Мандельброта


Любителям фракталов и математических картинок известны фантастические изображения растений, полученные с помощью программ. Это так называемые L-системы. В основе их построения лежат два принципа. Первый – это так называемая «черепашья графика» (оператор draw) патриарха GWBASIC и его детей Turbo Basic и QBasic, когда движение рисуется пошагово в приращениях относительно текущей точки. Либо моделируется данное поведение, задавая движение в приращениях координат. Второй принцип – изюминка метода: каждое единичное движение заменяется на весь рисунок. Например, нарисуем вилку-рогатульку. На следующем шаге работы программы каждая из трех палочек вилки заменяется такой-же вилкой, превращая вилку в ветку с сучками, после следующего шага получим лохматый куст, потом пушистое дерево, красивое, фрактальное. Меняя вид начальной картинки можно получать самые разные изображения от зонтиков укропа до колючего перекати-поле или пучка водорослей.
Кривая Коха Кривая Коха.— фрактальная кривая, описанная в 1904 году шведским математиком Хельге фон Кохом.Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую, называемую снежинкой Коха. Процесс построения - берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д. Кривая Коха нигде не дифференцируема и не спрямляема, Кривая Коха не имеет самопересечений, Кривая Коха имеет промежуточную размерность которая равна ln4/ln3.

Фрактальная размерность Фракта́льная разме́рность— один из способов определения размерности множества в метрическом пространстве

Фрактальный кластер Фрактальный кластер – скопление близко расположенных, тесно связанных друг с другом частиц любой природы общим количеством от 2 до 100 частиц.Основная черта фрактального кластера – средняя плотность частиц в нем p(r) =const/ra, где r-расстояние до центра. Число частиц N пропорционально RD, где D – фрактальная размерность кластера. Размерность кластера D не зависит ни от его формы, ни от типа упаковки в нем частиц. Она служит лишь количественной характеристикой того, как кластер заполняет занимаемое им пространство. Если в окрестность точки, занятой кластером, выделить область относительно небольшого объема, то попадающие в него участки кластера будут подобны в физическом смысле.
Методы моделирования процессов роста фрактальных структур Процесс роста в природе может приводить к образованию расползающихся разреженных структур, называемых фрактальными. На примере одной из разновидностей фрактального роста можно объяснить такие непохожие физические явления, как образование кристаллов и движение воздушных пузырьков в жидкости
Методы определения фрактальной размерности К настоящему времени разработано довольно много методов измерения фрак- тальной размерности, которые можно разделить на геометрические (метод остро- вов среза, Фурье анализ профилей, метод вертикальных сечений, метод подсчета числа ячеек и пр.) и физические, связанные с использованием на первой ступени сложной физической аппаратуры (ртутная порометрия, растровая электронная и просвечивающая электронная микроскопии, атомно-силовая микроскопия, вторич- ная электронная эмиссия, малоугловое рассеяние электронов и нейтронов и т.д.). Получаемая с помощью физических методов информация о характеристиках объ- екта носит косвенный характер и требует дополнительной обработки и осмысле- ния, поэтому физические методы особой популярностью не пользуются.
Перколяция В физике и химии явлением перколяции (от лат. percōlāre, просачиваться, протекать) называется явление протекания или непротекания жидкостей через пористые материалы, электричества через смесь проводящих и непроводящих частиц и другие подобные процессы. Теория перколяции находит применение в описании разнообразных систем и явлений, в том числе таких, как распространение эпидемий и надежность компьютерных сетей. Явление перколяции (или протекания среды) определяется:
Средой, в которой наблюдается это явление;
Внешним источником, который обеспечивает протекание в этой среде;
Способом протекания
среды, который зависит от внешнего
источника.

Метод вязких пальцев Метод вязких пальцев. При контакте двух подобных разнородных жидкостей поверхнось их раздела для двухмерной задачи в случае покоя определяется действием капиллярных сил,и между двумя жидкостями существует разность давлений. Если вязкость вытесняющей жидкости меньше вязкости вытесняемой жидкости,то граница раздела двух жидкостей оказывается неустойчивой. При описании такого рода неустойчивостей был предложен термин «образование вязких пальцев». Вследствие неустойчивости динамики движения границы некоторые области начнут двигаться быстрее,образуя пальцы, палец движется в ту сторону,в которую движется фронт вытеснения,опережая остальную его часть. Наибольший градиент давления в сильно вязкой жидкости образуется на конце пальца,этот град. Индуцирует иакс. Скор. Течения жидкости непосредственно перед самым длинным пальцем,который растет быстрее чем фронт в среднем,а такая ситуация неустойчива. Как только этот самый большой палец достигает определенных размеров, весь процесс повторяется на его границе и образуется ветвистая стр-ра.
Методы получения фрактальных структур В качестве первого примера рассмотрим более подробно образование фрактальных агрегатов кобальта. Малые частицы кобальта получали при испарении металла в атмосфере аргона при давлении 0,25-10 торр. Испарение металла осуществлялось с помощью нагретой вольфрамовой спирали. Конденсат металлических частиц в виде фрактальных образований собирался на медной сетке, покрытой углеродом. Средняя толщина металлического осадка составляла 10-200 мкм, причем относительный объем частиц кобальта в этом слое был в пределах 10- 2-10- 4, то есть осадок имел пористую структуру и основной объем занимали поры. Средний радиус частиц в этих образованиях увеличивался с ростом давления аргона. Фрактальная размерность агрегатов была в пределах 1,75-1,9 при давлении аргона в 0,9-8 торр, средний радиус частиц - менее 0,8 нм.
Фрактальные агрегаты могут быть получены также путем сжигания смеси в горящем пламени, если обеспечиваются условия конденсации и образования твердых частиц. Этот метод используется для получения фрактальных агрегатов SiO2 . С этой целью в водородно-кислородном пламени сжигался SiH4 . Образующийся при сжигании порошок содержит фрактальные агрегаты, состоящие из ї 103 частиц, радиус которых был в пределах 8-10 нм. Фрактальная размерность агрегатов D = 1,8-2,0. Сами частицы имели внутреннюю структуру, поскольку удельная поверхность образующихся частиц в 1,8-3,0 раза превышает поверхность частиц, являющихся сплошными. С ростом размера фрактального агрегата падают его плотность и прочность. Максимальный размер фрактальных агрегатов - микроны, а максимальное число частиц в них ї 104.
Полученные путем конденсации в газовой среде фрактальные агрегаты имеют очень высокую степень пористости. Объемная доля твердого вещества обычно составляет 10- 2-10- 4. Определение каких-либо свойств твердого тела становится при этом чрезвычайно затруднительным и в большинстве случаев даже невозможным. Поэтому актуальным является поиск способов и методов создания в твердых телах управляемой фрактальной структуры.
Понятие мультифрактала Мультифрактал. — комплексный фрактал, который может детерминироваться не одним единственным алгоритмом построения, а несколькими последовательно сменяющими друг друга алгоритмами. Каждый из них генерирует паттерн со своей фрактальной размерностью. Для описания мультифрактала вычисляют мультифрактальный спектр включающий в себя ряд фрактальных размерностей присущих элементам данного мультифрактала. Практика показала, что фрактальные множества, представляющие собой реальные физические системы, характеризуются не только одним значением размерности D, а целым их спектром. Что и привело к необходимости введения концепции мультифрактала, который можно представить, как суперпозицию монофракталов с различными D. Основной идеей мультифрактального подхода является построение каким-либо способом меры множества, аппроксимирующего данную структуру.
Открытые и
закрытые системы. Линейные и нелинейные
системы.



Динамические системы. Консервативные системы Динамическая система — множество элементов, для которого задана функциональная зависимость между временем и положением в фазовом пространстве каждого элемента системы. Данная математическая абстракция позволяет изучать и описывать эволюцию систем во времени.
Состояние динамической системы в любой момент времени описывается множеством вещественных чисел (или векторов), соответствующим определённой точке в пространстве состояний. Эволюция динамической системы определяется детерминированной функцией, то есть через заданный интервал времени система примет конкретное состояние, зависящее от текущего. Консервативная система — физическая система, работа неконсервативных сил которой равна нулю и для которой имеет место закон сохранения механической энергии, то есть сумма кинетической энергии и потенциальной энергии системы постоянна.
Примером консервативной системы служит солнечная система. В земных условиях, где неизбежно наличие сил сопротивления (трения, сопротивления среды и др.), вызывающих убывание механической энергии и переход её в другие формы энергии, например в тепло, консервативные системы осуществляются лишь грубо приближённо. Например, приближённо можно считать консервативной системой колеблющийся маятник, если пренебречь трением в оси подвеса и сопротивлением воздуха.
Эволюция нелинейных
систем


Фазовое пространство и фазовая траектория Фазовое пространство в математике и физике — пространство, на котором представлено множество всех состояний системы так, что каждому возможному состоянию системы соответствует точка фазового пространства.
Сущность понятия фазового пространства заключается в том, что состояние сколь угодно сложной системы представляется в нём одной единственной точкой, а эволюция этой системы — перемещением этой точки. Кроме того, в механике движение этой точки определяется сравнительно простыми уравнениями Гамильтона, анализ которых позволяет делать заключения о поведении сложных механических систем. Изменение состояния системы отображается на фазовой плоскости движением этой точки. След от движения изображающей точки называется фазовой траекторией.
Понятие аттрактора Аттрактор (англ. attract — привлекать, притягивать) — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности. Аттрактором может являться притягивающая неподвижная точка, периодическая траектория, или некоторая ограниченная область с неустойчивыми траекториями внутри. Аттракторы классифицируют по:1 Формализации понятия стремления: различают максимальный аттрактор, неблуждающее множество, аттрактор Милнора, центр Биркгофа, статистический и минимальный аттрактор.2 Регулярности самого аттрактора: аттракторы делят на регулярные (притягивающая неподвижная точка, притягивающая периодическая траектория) и странные (нерегулярные — зачастую фрактальные).3 Локальности («притягивающее множество») и глобальности. Аттрактор полагается замкнутым и (полностью) инвариантным множеством.
1. Принцип действия и устройство биполярного транзистора Биполя́рный транзи́стор — трёхэлектродный полупроводниковый прибор, один из типов транзисторов. В полупроводниковой структуре сформированы два p-n-перехода, перенос заряда через которые осуществляется носителями двух полярностей — электронами и дырками. Именно поэтому прибор получил название «биполярный» (от англ. bipolar), в отличие от полевого (униполярного) транзистора. В активном усилительном режиме работы транзистор включён так, что его эмиттерный переход смещён в прямом направлении[2] (открыт), а коллекторный переход смещён в обратном направлении (закрыт).
В транзисторе типа n-p-n[3] основные носители заряда в эмиттере (электроны) проходят через открытый переход эмиттер-база (инжектируются) в область базы. Часть этих электронов рекомбинирует с основными носителями заряда в базе (дырками). Однако, из-за того, что базу делают очень тонкой и сравнительно слабо легированной, бо́льшая часть электронов, инжектированных из эмиттера, диффундирует в область коллектора, так как время рекомбинации относительно велико[4]. Сильное электрическое поле обратносмещённого коллекторного перехода захватывает неосновные носители из базы (электроны) и переносит их в коллекторный слой. Ток коллектора, таким образом, практически равен току эмиттера, за исключением небольшой потери на рекомбинацию в базе, которая и образует ток базы (Iэ=Iб + Iк).
Коэффициент α, связывающий ток эмиттера и ток коллектора (Iк = α Iэ), называется коэффициентом передачи тока эмиттера. Численное значение коэффициента α = 0,9—0,999. Чем больше коэффициент, тем эффективней транзистор передаёт ток. Этот коэффициент мало зависит от напряжения коллектор-база и база-эмиттер. Поэтому в широком диапазоне рабочих напряжений ток коллектора пропорционален току базы, коэффициент пропорциональности равен β = α/(1 − α), от 10 до 1000. Таким образом, малый ток базы управляет значительно бо́льшим током коллектора.
2. Принцип действия и устройство полевого транзистора с управляющим р-п переходом Полевой транзистор с управляющим р-n- переходом – это полевой транзистор, затвор которого отделен в электрическом отношении от канала р-n-переходом, смещенным в обратном направлении.
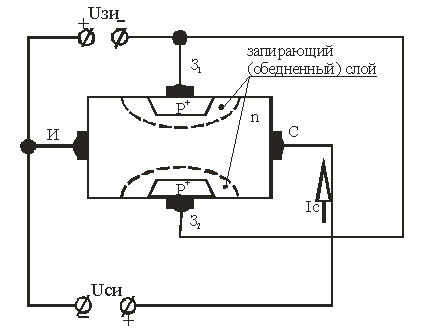
Рисунок 1 – Устройство полевого транзистора с управляющим р-n-переходом (каналом n- типа)

Рисунок 2 – Условное обозначение полевого транзистора с р-n-переходом и каналом n- типа (а), каналом р- типа (б)
Каналом полевого транзистора называют область в полупроводнике, в которой ток основных носителей заряда регулируется изменением ее поперечного сечения.
Электрод (вывод), через который в канал входят основные носители заряда, называют истоком. Электрод, через который из канала уходят основные носители заряда, называют стоком. Электрод, служащий для регулирования поперечного сечения канала за счет управляющего напряжения, называют затвором.
Как правило, выпускаются кремниевые полевые транзисторы. Кремний применяется потому, что ток затвора, т.е. обратный ток р-n- перехода, получается во много раз меньше, чем у германия.
Условные обозначения полевых транзисторов с каналом n- и р- типов приведены на рис. 2.
Полярность внешних напряжений, подводимых к транзистору, показана на рис. 1. Управляющее (входное) напряжение подается между затвором и истоком. Напряжение Uзи является обратным для обоих р-n- переходов. Ширина р-n- переходов, а, следовательно, эффективная площадь поперечного сечения канала, его сопротивление и ток в канале зависят от этого напряжения. С его ростом расширяются р-n- переходы, уменьшается площадь сечения токопроводящего канала, увеличивается его сопротивление, а, следовательно, уменьшается ток в канале. Следовательно, если между истоком и стоком включить источник напряжения Uси, то силой тока стока Iс, протекающего через канал, можно управлять путем изменения сопротивления (сечения) канала с помощью напряжения, подаваемого на затвор. На этом принципе и основана работа полевого транзистора с управляющим р-n- переходом.
