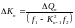Далее приводим полученные выражения для переменной жесткости, квадратичной функции прогиба и уравнение изгиба пластинки из нелинейно-деформируемого материала к безразмерному виду:
Квадратичная функция прогиба пластинки в безразмерном виде выглядит следующим образом:
Выражение для переменной вдоль пространственных координат жесткости пластинки в безразмерном виде выглядит в следующим образом:
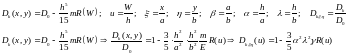
Переменная по длине пластинки жесткость в безразмерном виде:
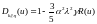
При использовании коэффициентов заменяющих размерные координаты на безразмерные получим нелинейное дифференциальное уравнение изгиба пластинки из нелинейно-деформируемого материала в безразмерном виде в инкрементальной форме метода последовательных нагружений:
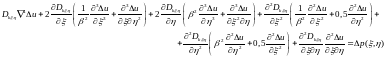где
.
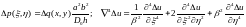Как видно, из приведенного выше уравнения для изгиба пластинки из нелинейно-деформируемого материала, требуется получить производные от переменной жесткости пластинки.
Первая производная от переменной жесткости пластинки по безразмерным пространственным координатам:
Вторая производная от переменной жесткости пластинки по безразмерным пространственным координатам:
Смешанная производная от переменной жесткости пластинки по безразмерным пространственным координатам:
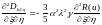
Подставляем полученные выше выражения для производных от переменной жесткости в уравнение изгиба пластинки:
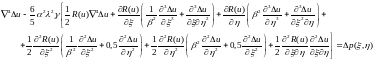
На втором этапе расчета необходимо определиться с построением и представлением функции аппроксимирующей прогиб и приращение прогиба пластинки из нелинейно-деформируемого материала. В данном случае представим прогиб и приращение прогиба пластинки в виде ряда с конечным числом членов:
,
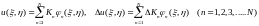где искомые постоянные
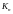будем
называть обобщенными координатами, а
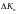будем называть приращениями обобщенных
координат, а функцию
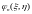- аппроксимирующей (координатной)
функцией (функцией, приближающей решение
к точному).
На третьем этапе алгоритма расчета условимся, что будем решать данную задачу в первом приближении метода Бубнова-Галеркина в инкрементальной форме, то есть u(ξ,η)=Ku1(ξ)u2(η) и Δu(ξ,η)=ΔKu1(ξ)u2(η).
Записываем уравнение метода Бубнова-Галеркина, которое будет выглядеть следующим образом:
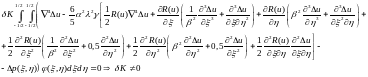
При удовлетворении условий получаем:
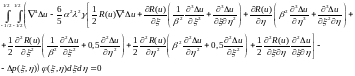
При подстановке в полученное выше уравнение метода Бубнова-Галеркина выражений для прогибов и приращений прогибов получим следующее:
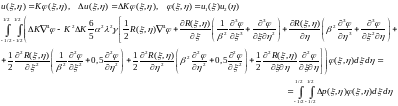Квадратичная
функция прогиба пластинки:
Бигармонический оператор Лапласа:
Разделим уравнение метода Бубнова-Галеркина на отдельные интегралы:
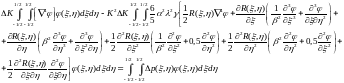
В результате получим уравнение метода Бубнова-Галеркина в виде:
Коэффициенты которого равны:
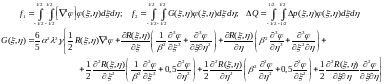
Приведение коэффициента f2 к упрощенному виду:
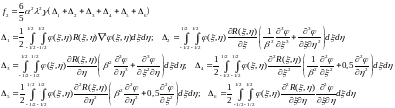Численная
реализация полученных аналитических
выражений
Исходные данные для пластинки:
Функция аппроксимирующая прогиб пластинки:
Определение обобщенной координаты K:
