Формула расчета индекса корреляции

Индекс корреляции принимает значение от 0 до 1. Чем выше значение индекса, тем ближе расчетные значения результативного признака к фактическим. Индекс корреляции используется при любой форме связи переменных, при парной линейной регрессии он равен парному коэффициенту корреляции

В качестве меры точности модели применяют различные точностные характеристики.

Точностные характеристики	Расчет и содержание характеристики
Максимальная ошибка	Соответствует максимальному отклонению расчетных значений от фактических
Средняя абсолютная ошибка	Ошибка показывает, насколько в среднем отклоняются фактические значения от модели
Дисперсия ряда остатков (остаточная дисперсия)	, где - среднее значение ряда остатков. Определяется по формуле:
Среднеквадратическая ошибка	Представляет собой корень квадратный из дисперсии Чем меньше значение ошибки, тем точнее модель
Средняя относительная ошибка аппроксимации	Допустимый предел значений не более 8-15%

Если модель регрессии признана адекватной, а параметры модели значимы, то переходят к построению прогноза.

Прогнозируемое значение переменной y получается при подстановке в уравнение регрессии ожидаемой величины независимой переменной .

Данный прогноз называется точечным. Вероятность реализации точечного прогноза практически равна нулю. Поэтому рассчитывается доверительный интервал прогноза с большой надежностью.

Доверительные интервалы прогноза зависят от стандартной ошибки, удаления от своего среднего значения , количества наблюдений n и уровня значимости прогноза .

Понятие нелинейных моделей и их линеаризация

Соотношение между социально-экономическими явлениями и процессами далеко не всегда можно выразить линейными функциями. Так, например, нелинейными оказываются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства – трудом, капиталом и т.д.), функции спроса (зависимость между спросом на товары, услуги и их ценами или доходом) и другие.

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Нелинейность может проявляться как относительно переменных, так и входящих в функцию коэффициентов (параметров).

Различают два класса нелинейных регрессий.

Для оценки параметров нелинейных моделей используются два подхода. Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными.

Второй подход обычно применяется в случаях, когда подобрать соответствующее линеаризующее преобразование не удается. Тогда применяются методы нелинейной оптимизации на основе исходных переменных.

Наиболее часто применяемые в экономическом анализе виды нелинейных регрессий следующие: полином второго порядка, гипербола, степенная и показательная функции.

Оценка параметров нелинейной регрессии по переменным, включенным в анализ, но линейным по оцениваемым параметрам, определяется методом наименьших квадратов (МНК) путем решения нормальных уравнений.
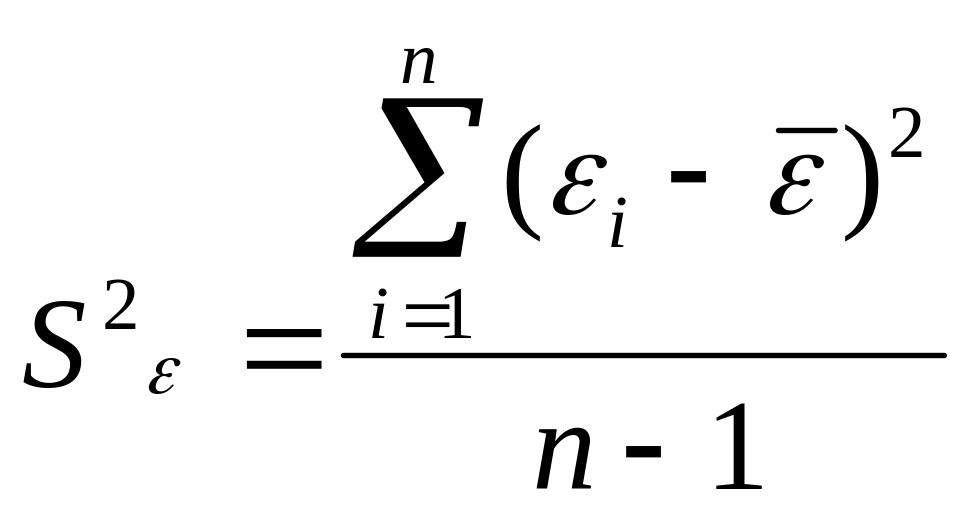