Расчётная таблица

Годы	обеспеченность жильем на конец года, м2	t i	t i2	yi·ti	теоретические значения тренда	отклонение от тренда ui	отклонение ui2	ui*ui+1
2000	19,2	-3	9	-57,6	19,0	0,2	0,04	0,02
2001	19,5	-2	4	-39	19,4	0,1	0,01	0
2002	19,8	-1	1	-19,8	19,8	0,0	0	0
2003	20,2	0	0	0	20,2	0,0	0	0
2004	20,5	1	1	20,5	20,6	-0,1	0,01	0,01
2005	20,9	2	4	41,8	21,0	-0,1	0,01	0,01
2006	21,3	3	9	63,9	21,4	-0,1	0,01	-
Итого	141,4	0	28	9,8	141,4	0,0	0,08	0,04

Система нормальных уравнений имеет вид:

Таким образом, обеспеченность жильём за последние семь лет возрастала в среднем за год на 0,4 м².

В таблице 5.5 приведены теоретические значения уравнения тренда с целью расчёта отклонений фактического уровня ряда от теоретического.

Расчёт ошибки репрезентативности коэффициента линейного тренда определим по формуле

Параболический тренд обычно выражается параболой II порядка, уравнение которой имеет вид:

ŷ_i = а₀ + а₁ · t_i +а₂·t²

Значения параметров параболы второго порядка такие же, как и в уравнении прямой, кроме а₁, а₂. Они имеют следующее выражение:

Параметр уравнения	Содержание параметра
а0	– коэффициент тренда, численно равный среднему выровненному уровню для момента или периода времени, принятого за начало отсчёта (ti = 0);
а1	- коэффициент тренда, характеризующий средний за весь период среднегодовой прирост, который уже не является константой, а изменяется равномерно со средним ускорением, равным 2а2;
а2	- главный параметр уравнения, константа, характеризующий ускорение

Тренд в форме параболы второго порядка применяют для отображения тенденций динамики, для которых на некотором, как правило непродолжительном, этапе развития свойственно примерно постоянное ускорение абсолютных изменений уровней.

Рис. 5.3. Динамика средних экспортных цен на природный газ по данным платежного баланса Российской Федерации, долл за 1 м³

Тренд в форме параболической линии обладает рядом свойств:

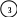
Для вычисления параметров а₀, а₁, а₂ по методу наименьших квадратов строят следующую систему нормальных уравнений с тремя неизвестными:

При переносе начала отсчёта периодов (моментов) времени в середину ряда, суммы нечетных степеней номеров этих периодов Σ t_i и Σ t_i³ равняются нулю. Второе уравнение, следовательно, становится уравнением с одним неизвестным:

Параметр уравнения	Содержание параметра
а1	- коэффициент тренда, характеризующий средний за весь период среднегодовой прирост, который уже не является константой, а изменяется равномерно со средним ускорением;

Отсюда можно выразить параметр а₁ :

а₁ =

Оставшиеся уравнения образуют систему двух уравнений с двумя неизвестными:

Параболическое уравнение тренда достаточно редко встречается в анализе экономических явлений и процессов.

Одной из простых форм гиперболы является уравнение, имеющее вид:

ŷ_i = а₀ +

где:

Параметр	Содержание параметра
а0	свободный член гиперболы, предел к которому стремится уровень ряда;
а1	основной параметр гиперболы. Если а1 > 0, то этот тренд выражает тенденцию замедляющегося снижения уровней и при t → ∞, ŷi → а0. Если параметр а1< 0, то с возрастанием t, т.е. с течением времени, уровни тренда возрастают и стремятся к величине а0 при t → ∞

При расчёте гиперболического тренда нельзя нумеровать года от середины ряда, так как значения должны быть всегда положительными.

Гиперболический тренд, также как и другие виды трендов, обладает рядом свойств:

Экспоненциальным трендом называют тренд, который выражается следующим уравнением:

или

где:

Параметр	Содержание параметра
k	постоянный темп изменения уровней (цепной). Если к>1, то имеется тренд с возрастающими уровнями, при чем это возрастание не просто ускоренное, а с возрастающим ускорением и возрастающими производными всех более высоких порядков. Если к<1, то имеется тренд, выражающий тенденцию постоянного, но замедляющегося сокращения уровней, причем замедление непрерывно усиливается. Экстремума экспонента не имеет и при t→∞ стремится либо к ∞ при к>1, либо к 0 при к<1.
а	свободный член экспоненты, равен выровненному уровню, то есть уровню тренда в момент или период, принятый за начало отсчёта времени (при t=0)

Экспоненциальный тренд характерен для процессов, развивающихся в среде, не создающих никаких ограничений для роста уровней. Следовательно, на практике такие явления встречаются только в ограниченном промежутке времени, так как любая среда рано или поздно создаёт ограничения.

Экспоненциальный тренд обладает рядом свойств:

Уравнение логарифмического тренда применяют в том случае, когда изучаемый процесс приводит к замедлению роста какого-либо показателя, но при этом рост не прекращается, а стремится к какому-либо ограниченному пределу. В этом случае ни гиперболическая форма тренда, ни парабола с отрицательным ускорением не подходят. Логарифмы возрастают значительно медленнее, чем сами числа (номера периодов t), но рост логарифмов не ограничен. Подбирая начало отсчёта периодов (моментов) времени, можно найти такую скорость снижения абсолютных изменений, которая наилучшим образом отвечает фактическому временному ряду.

Логарифмический тренд выражается следующей формулой:

ŷ_i = а₀ + а₁·ln t_i

Логарифмический тренд обладает следующими свойствами:

Логарифмический тренд, как и гиперболический, отражает постепенно затухающий процесс изменений. Однако эти тренды имеют существенное различие:

Затухание по гиперболе происходит быстро при приближении к конечному пределу, а при логарифмическом тренде затухающий процесс продолжается без ограничения гораздо медленнее

Логистическая форма тренда используется для описания таких процессов, при которых изучаемый показатель проходит полный цикл развития, начиная, от нулевого уровня, сначала медленно, но с ускорением возрастая, затем ускорение становится нулевым в середине цикла, то есть рост происходит по линейному тренду, далее, в завершающей части цикла, рост замедляется по гиперболе по мере приближения к предельному значению показателя.

Если диапазон изменения уровней от 0 до 1, то уравнение логистического тренда имеет вид (1), если же диапазон изменения уровней ограничен не нулём, а любыми значениями, определяемыми исходя из существа задачи, обозначаемыми у_max и у_min, то формула логистического тренда примет вид (2):

При разных значениях параметров логистического уравнения (а₀ и а₁) будут получаться разные виды трендов:

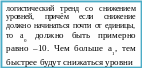
Для правильного выбора типа тренда, который наилучшим образом отражает тенденцию фактического ряда уровней, используют несколько методов распознавания типов тренда. Основными, и наиболее распространенными выступают: графический метод и проверка статистических гипотез о типе тренда.