Основные виды тренда

Общие составляющие тренда

Основной составляющей является тренд. Значения сезонной и случайной компонент остаются после выделения из него трендовой составляющей.

В случае, если все составляющие компоненты найдены верно, то математическое ожидание случайной компоненты равно нулю и ее колебания около среднего значения постоянны.

Графическое изображение составляющих тренда

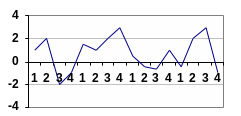
Пример 5.3. Пример 5.4. Пример 5.5

Уровни временного ряда можно представить как сумму или произведение всех его составляющих компонент (трендовой, сезонной и случайной). Модель, в которой все компоненты ряда динамики представлены как сумма этих составляющих, называют аддитивной. В случае, если факторы влияния представлены как произведение составляющих, то модель называют мультипликативной.

Модели составляющих компонент

В эконометрическом исследовании проводят количественную оценку каждой из перечисленных компонент по выбранной модели.

Во временных рядах обычно различают тенденции трех видов:

Прежде чем выделять тренд необходимо проверить гипотезу о его наличии. На практике различают несколько критериев для проверки наличия тренда, но основными выступают два: метод разности средних двух разных частей одного и того же ряда и метод Фостера - Стюарта.

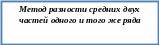
Расчетное значение критерия Стьюдента определяется по формуле:

где:

- средние для каждой части временного ряда;

n₁, n₂ – число наблюдений в каждой из частей ряда;

σ – среднее квадратическое отклонение разности средних.

Табличное значение критерия Стьюдента выбирается с числом степеней свободы, затем определяется среднее квадратическое отклонение.

Параметр	Содержание параметра
Число степеней свободы	υ= n1 + n2 -2
Среднее квадратическое отклонение разности средних	. Для расчета дисперсий в каждой части временного ряда выбирается число степеней свободы (n1-1) и (n2-1). Соответственно сама дисперсия i-ой части временного ряда определяется по формуле: , i = 1,2,…,n. Гипотезу о равенстве дисперсий проверяют с помощью критерия Фишера: F = . Если фактическое значение критерия Фишера меньше табличного значения, при заданном уровне вероятности, то гипотеза о равенство дисперсий принимается. Если фактическое значение критерия Фишера больше табличного, то гипотеза о равенстве дисперсий отвергается и тогда критерий Стьюдента для проверки существенности разности средних не может быть использован

При использовании метода Фостера – Стюарта вычисления строят в определенной последовательности:

Самым простым типом линии тренда является прямая линия, которая описывается линейным уравнением тренда.

ŷi = а0 + а1 · ti , где ŷi – выровненные (теоретические) уровни тренда для лет с номером i; ti – номера моментов или периодов времени, к которым относятся уровни временного ряда (год, месяц, др.); а0, а1 – параметры тренда
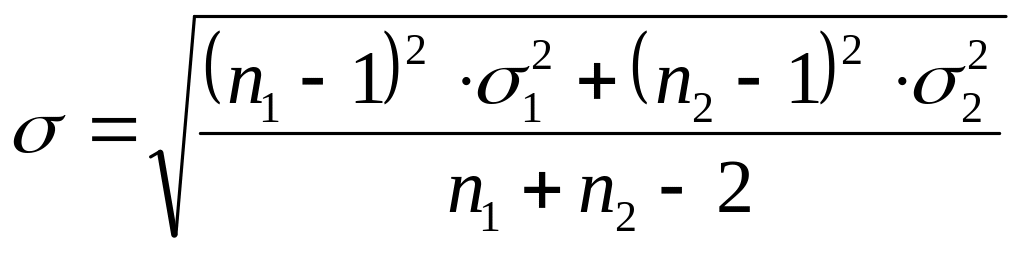