

частину рідини, що лежить над площиною, із силою Fтр , причому величини Fтр і Fтр′
визначаються формулою (38.1). Таким чином, формула (38.1) визначає не тільки силу тертя, що діє на пластини, але й силу тертя між дотичними частинами рідини.
Якщо досліджувати швидкість частинок рідини в різних шарах, то виявляється, що вона змінюється в напрямку Z , який перпендикулярний до пластин (рис. 38.1), за лінійним законом
υ(z) = |
|
υ0 |
|
z . |
(38.2) |
||
|
|
||||||
|
|
|
|
d |
|
||
Частинки рідини, яка безпосередньо дотикаються до пластинки, як би прилипають до |
|||||||
них, мають таку ж швидкість, як і самі пластини. Формулу (38.2) можемо перетворити |
|
||||||
|
dυ |
= |
|
υ0 |
. |
(38.3) |
|
|
|
|
|||||
|
dz |
|
d |
|
|||
Використавши рівність (38.3), формулі (38.1) для сили внутрішнього тертя можна надати вигляд
|
dυ |
|
|
|
||
Fтр = η |
|
S |
. |
(38.4) |
||
dz |
||||||
|
|
|
|
|
||
|
|
|
|
|
|
|
Формулу (38.4) отримав Ньютон і тому її називають формулою Ньютона для сили внутрішнього тертя. Величина dυ / dz показує, як швидко змінюється швидкість у
напрямку осі Z , і називається градієнтом швидкості (точніше, це – модуль градієнта швидкості; сам градієнт є вектором).
Формула (38.4) була нами отримана для випадку, коли швидкість змінюється за лінійним законом (у цьому випадку градієнт швидкості є постійним). Виявляється, що ця формула залишається справедливою й для будь-якого іншого закону зміни швидкості при переході від одного шару рідини до іншого. У цьому разі для визначення сили тертя між двома сусідніми шарами рідини потрібно брати значення градієнта dυ / dz у тому місці, де проходить уявна поверхня розділу шарів.
Усе, що було сказане в цьому параграфі відноситься не тільки до рідин, але й до газів. Одиницею в'язкості в СІ є така в'язкість, при якій градієнт швидкості, що дорівнює 1 м/с на 1 м, приводить до виникнення сили внутрішнього тертя в 1 Н на 1 м2 поверхні дотику
шарів рідини. Ця одиниця позначається Н·с/м2.
Коефіцієнт в'язкості залежить від температури, причому характер цієї залежності істотно різний для рідин і газів. У рідин коефіцієнт в'язкості сильно зменшується з підвищенням температури. У газів, навпаки, коефіцієнт в'язкості з температурою росте. Відмінність у характері поведінки η при змінах температури вказує на різні механізми
внутрішнього тертя в рідинах і газах.
2 Спостерігається два види течії рідини (або газу). В одних випадках рідина як би розділяється на шари, які ковзають один відносно одного, не перемішуючись. Така течія називається ламінарною. Якщо в ламінарний потік увести підфарбований струмок, то він буде зберігатися, не розмиваючись, на всій довжині потоку, тому що частинки рідини в ламінарному потоці не переходять із одного шару в іншій. Ламінарна течія є стаціонарною.
При збільшенні швидкості або поперечних розмірів потоку характер течії істотно змінюється. Виникає енергійне перемішування рідини. Така течія називається турбулентною. При турбулентній течії швидкість частинок у кожному місці увесь час змінюється хаотичним чином – течія є нестаціонарною. Якщо в турбулентний потік увести пофарбований струмок, то вже на невеликій відстані від місця її введення пофарбована рідина рівномірно розподіляється по всьому перетині потоку.
Англійський учений Рейнольдс встановив, що характер течії залежить від значення безрозмірної величини:
61

Re = |
ρυl |
, |
(38.5) |
η |
де ρ – густина рідини (або газу); υ – середня за перерізом швидкість потоку; η – в'язкість
рідини; l – характерний для поперечного перерізу потоку розмір, наприклад, сторона квадрата при квадратному розтині, радіус або діаметр при круглому розтині. Величина Re ,
що визначається формулою (38.1), називається числом Рейнольдса.
При малих значеннях Re течія носить ламінарний характер. Починаючи з деякого значення Re , яке називають критичним, течія стає турбулентною. Якщо за характерний розмір труби взяти її радіус (у цьому випадку Re = ρυr / η ), то критичне значення числа
Рейнольдса буде дорівнювати приблизно 1000 (якщо за l взяти діаметр труби, то критичне значення Re буде дорівнювати 2000).
Число Рейнольдса служить критерієм подібності для течії рідин у трубах, каналах і т.д. Наприклад, характер течії різних рідин (або газів) у круглих трубах різних діаметрів буде однаковим, якщо кожній течії відповідає однакове значення Re .
У число Рейнольдса входить відношення густини ρ й в'язкості η. Величина
ν = |
η |
(38.6) |
|
ρ |
|
називається кінематичною в'язкістю. Щоб відрізнити в’язкість η від ν , величину η
називають динамічною в'язкістю. Число Рейнольдса, яке виражено |
через кінематичну |
|
в'язкість, має вигляд |
|
|
Re = |
υl . |
(38.7) |
|
ν |
|
§ 39 Рух тіл у рідинах та газах. Сила лобового опору. Піднімальна сила. Парадокс Д’Аламбера. Вплив в’язкості на характер обтікання тіла рідиною. Сила Стокса [4]
1 Вплив рідкого або газоподібного середовища на тіло, яке рухається в ньому з постійною швидкістю υ, буде таким самим, як і була б дія на нерухоме тіло з боку набігаючої на нього зі швидкістю υ однорідного потоку рідини або газу (надалі для стислості ми будемо говорити тільки про рідину, маючи на увазі при цьому й гази). Отже, при з'ясуванні сил, що діють на тіло, байдуже, що вважати рухомим – тіло або середовище. Зручно припускати тіло нерухомим, а середовище рухомим.
Силу F , з якої потік діє на тіло, можна розкласти на дві складові: силу X , яка направлена уздовж швидкості υ незбуреного потоку, і яку називають лобовим опором, й
силу Y , яка перпендикулярна до υ, і яку називають піднімальною силою. Лобовий опір складається із сил тиску й сил внутрішнього тертя. Очевидно, що на тіло, яке симетричне відносно напрямку швидкості потоку υ, може діяти тільки лобовий опір, піднімальна ж сила в цьому разі буде відсутня.
2 Можна довести, що в ідеальній рідині, яка |
|
|
|
|
|
нестискується, рівномірний рух тіла довільної форми повинен |
|
|
|
2 |
|
відбуватися без лобового опору. Цей результат отримав назву |
|
|
1 |
3 |
|
|
|
||||
парадокса Д’Аламбера. |
|
|
|
4 |
|
Покажемо відсутність лобового опору на прикладі |
|
|
|
|
|
обтікання ідеальною рідиною дуже довгого («нескінченного») |
Рисунок 39.1 – Обтікан- |
||||
циліндра (рис. 39.1). Не маючи в'язкості, ідеальна рідина |
ня циліндра |
ідеальною |
|||
повинна ковзати по поверхні циліндра, повністю обтікаючи |
рідиною |
|
|
||
його. Тому лінії течії будуть симетричними як відносно прямої, |
|
|
|
|
|
62 |
|
|
|
|
|
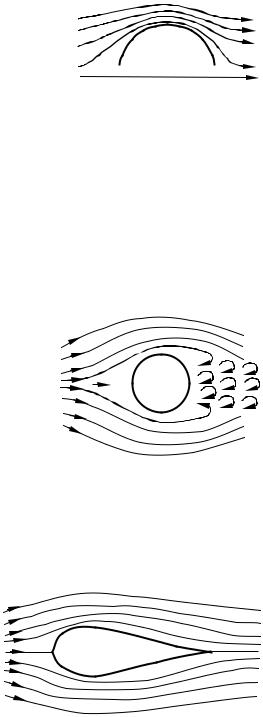
що проходить через точки 1 і 3, так і відносно прямої, що проходить через точки 2 і 4. Теорема Бернуллі дозволяє за картиною ліній течії судити про тиск у різних точках потоку. Поблизу точок 1 і 3 тиск однаковий (і більший, ніж у незбуреному потоці, тому що швидкість поблизу цих точок менша). Поблизу точок 2 і 4 тиск також однаковий (і менший, ніж у незбуреному потоці, тому що швидкість поблизу цих точок більша). Отже, результуюча сила тиску на поверхню циліндра (яка під час відсутності в'язкості могла б обумовити лобовий опір) буде дорівнювати нулю. Як ми вже відзначали, такий же самий результат виходить і для тіл довільної (у тому числі й несиметричної) форми. Цей висновок стосується тільки лобового опору. Піднімальна сила, дорівнює нулю для симетричних тіл
(див. рис. 39.1), для несиметричних тіл вона відмінна від нуля. |
|
|
|
|
|
|
||||||||||||
На рис. 39.2 показані лінії течії при обтіканні |
|
|
|
|
|
|
||||||||||||
ідеальною рідиною напівциліндра. Внаслідок повного |
|
|
|
2 |
|
|
||||||||||||
обтікання |
лінії |
течії |
симетричні |
відносно |
|
прямої, |
|
що |
|
|
1 |
4 |
3 |
|
||||
проходить через точки 2 і 4. Однак відносної прямої, що |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||
проходить |
через точки |
1 |
і |
3, |
картина |
ліній |
течії |
Рисунок 39.2 – Виникнення |
||||||||||
несиметрична. |
Поблизу |
точки |
2, |
де лінії |
густіші, |
тиск |
||||||||||||
піднімальної |
сили Y при |
|||||||||||||||||
менший, ніж поблизу точки |
4, |
у результаті |
чого виникає |
|||||||||||||||
обтіканні |
|
|
ідеальною |
|||||||||||||||
піднімальна сила. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
рідиною |
несиметричного |
||||||||
3 Інакше |
відбувається |
рух тіла у в’язкій рідині. |
У |
|||||||||||||||
тіла |
|
|
|
|
||||||||||||||
цьому випадку |
дуже |
тонкий |
шар рідини |
|
прилипає |
до |
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||
поверхні тіла й рухається з ним як одне ціле, захоплюючи за собою через внутрішнє тертя наступні шари. У міру видалення від поверхні тіла швидкість шарів стає усе менше й, нарешті, на деякій відстані від поверхні рідина буде не збурена рухом тіла. Таким чином,
тіло виявляється оточеним шаром рідини зі швидкістю, яка змінюється всередині цього шару досить швидко. Цей шар називається пограничним. У ньому діють сили в’язкого тертя, які в остаточному підсумку прикладені до тіла й приводять до виникнення лобового опору.
Але вплив в'язкості не вичерпується виникненням сил |
|
|
|
|
тертя. Наявність пограничного шару в повністю змінює |
|
|
|
|
характер обтікання тіла рідиною. |
|
|
|
2 |
Повне обтікання стає неможливим. Дія сил тертя в |
|
|
1 |
3 |
|
||||
пограничному шарі приводить до того, що потік |
|
|
|
4 |
відривається від поверхні тіла, у результаті чого за тілом |
|
|
|
|
виникають вихри (рис. 39.3). Вихри несуться потоком і |
|
|
|
|
поступово загасають внаслідок тертя; при цьому енергія |
|
|
|
|
вихрів витрачається на нагрівання рідини. Тиск, що |
Рисунок 39.3 |
– Обтікання |
||
утвориться за тілом, у вихровій області виявляється |
циліндра в’язкою рідиною |
|||
зниженим, внаслідок чого результуюча сил тиску буде |
|
|
|
|
відмінна від нуля. Це у свою чергу обумовлює лобовий опір.
Таким чином, як ми вже відзначали, лобовий опір складається з опору тертя й опору тиску. Опір тиску сильно залежить від форми тіла. Найменший опір тиску мають тіла з краплеподібною формою (рис. 39.4).
Співвідношення між опором тертя й опором тиску визначається значенням числа Рейнольдса
Re = ρυηl .
Тут υ – швидкість тіла відносно рідини (або швидкість потоку, що набігає на тіло); l – характерний розмір тіла, наприклад радіус для тіла кульової форми. При малих Re (тобто при малих υ і l ) основну роль відіграє опір тертя, так що опором
Рисунок 39.4 – Обтікання рідиною тіла краплеподібної форми
63
тиску можна знехтувати. З ростом в'язкості відносна роль сил тертя зростає. При великих значеннях Re у лобовому опорі переважають сили тиску.
4 Стокс установив, що при невеликих швидкостях і розмірах тіл (тобто при малих Re ,
коли опір середовища обумовлений практично тільки силами тертя) модуль сили опору визначається формулою
F = kηlυ |
, |
(39.1) |
де η – динамічна в'язкість середовища; υ – швидкість руху тіла; l – характерний розмір
тіла; k – коефіцієнт пропорційності, який залежить від форми тіла. Силу, що визначається
(39.1), називають силою Стокса.
Для кулі, якщо взяти за l його радіус r , коефіцієнт пропорційності дорівнює 6π .
Отже, сила опору руху в рідинах невеликих кульок при малих швидкостях дорівнює
F = 6πηrυ |
. |
(39.2) |
Силу, що визначається формулою (39.2), теж називають силою Стокса. Треба мати на увазі, що формула Стокса справедлива за умови, що відстань від тіла до границь рідини (наприклад, до стінок посудини) набагато більша розмірів тіла.
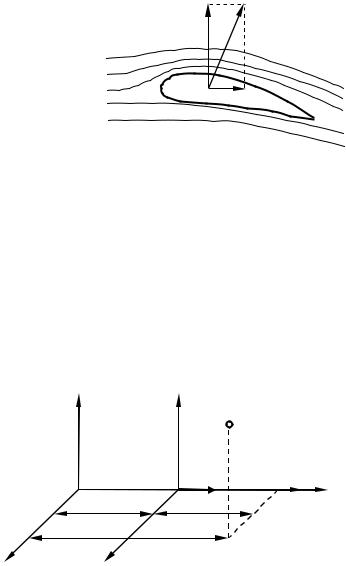
5 Літак підтримується в повітрі піднімальною |
|
r |
|
|
|
силою, що діє на його крила. Лобовий опір відіграє при |
|
Y |
|
|
|
польоті літака шкідливу роль. Тому крилам і фюзеляжу |
|
|
|
|
|
літака надають форму, завдяки якій газ його добре |
|
|
|
|
|
обтікає (рис. 39.5). Внаслідок асиметричної форми й |
|
|
r |
|
|
нахиленого розміщення крила швидкість повітря над |
|
|
X |
|
|
крилом виявляється більше (а, отже, тиск менше, як це |
|
|
|
|
|
випливає з рівняння Бернуллі), ніж під крилом. Завдяки |
|
|
|
|
|
цьому створюється піднімальна сила. Істотну роль в |
Рисунок |
39.5 |
– |
Обтікання |
|
утворенні піднімальної сили відіграє в'язкість повітря, |
повітрям |
крила |
літака: X – |
||
завдяки чому утворюються вихрі, які відриваються від |
лобовий |
опір, Y |
– |
піднімальна |
|
заднього краю крила. Детально розглянути явища, що |
|||||
сила |
|
|
|
||
обумовлюють піднімальну силу, тут ми, на жаль, не |
|
|
|
||
|
|
|
|
||
маємо можливості. Основи теорії крила літака створив у 1904 р. Жуковський, який сформулював теорему про піднімальну силу й довів формулу для визначення цієї сили, яка є основою всіх аеродинамічних розрахунків літаків.
|
|
|
ТЕМА 7 ЕЛЕМЕНТИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ |
|
|
||||||||
§ 40 Принцип відносності Галілея. Перетворення Галілея [4] |
|
|
|
|
|||||||||
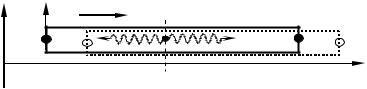
1 Порівняємо |
опис |
руху |
Y |
Y ¢ |
|
|
|
|
|||||
частинки |
в |
інерціальних системах |
|
|
|
P |
|
|
|||||
відліку |
K й |
K′ , які рухаються одна |
|
K |
K¢ |
|
|
||||||
|
|
|
|
||||||||||
відносно |
іншої зі |
швидкістю |
V |
|
|
r |
|
|
X ¢ |
||||
(рис. 40.1). |
|
Для |
|
спрощення |
|
|
|
X |
|||||
|
|
O |
O¢ |
V |
|
||||||||
математичних перетворень виберемо |
|
|
|
||||||||||
|
V ×t |
x′ |
|
|
|
||||||||
осі координат так, як показано на |
|
|
|
|
|||||||||
рисунку. Тут осі X й X ′ |
збігаються, |
|
x |
|
|
|
|
||||||
осі Y |
й |
Y ′ , а також |
Z |
і |
Z ′ |
Z |
Z ¢ |
|
|
|
|
||
паралельні одна одній. Відлік часу |
|
|
|
|
|||||||||
|
Рисунок 40.1 |
|
|
|
|||||||||
почнемо |
з |
того |
моменту, |
коли |
|
|
|
|
|||||
початок координат O і O′ збігалися. Тоді координати x й x′ довільно взятої точки P будуть пов’язані співвідношенням x = x′ +Vt . При обраному виборі осей y = y′ і z = z′ . У
64
ньютонівській механіці передбачається, що час у всіх системах відліку тече однаково: тому t = t′ . Таким чином, отримуємо чотири рівняння
x = x′ +Vt |
, |
y = y′ |
, |
z = z′ |
, |
t = t′ |
, |
(40.1) |
які називають перетвореннями Галілея. Ці рівняння дозволяють перейти від координат і часу однієї інерціальної системи відліку до координат і часу іншої інерціальної системи.
2 Продиференціюємо перше з рівнянь (40.1) за часом, |
взявши до уваги, що t = t′ й, |
||||||||||||||||||||||||||
отже, похідна за t збігається з похідною за t′ : |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
dx |
= |
dx′ |
+V = |
dx′ |
+V. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
dt |
dt |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt′ |
|
|
|
|
|
|
|
|
|
||||||||
Похідна |
dx / dt є проекцією швидкості частинки |
υ |
в системі |
K |
на вісь |
X |
цієї |
||||||||||||||||||||
системи; похідна dx′ / dt′ |
є проекцією швидкості частинки υ′ |
в системі |
K′ |
на вісь |
X ′ цієї |
||||||||||||||||||||||
системи. Отже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υx = υ′x′ +V , |
|
|
|
|
|
|
|
(40.2) |
|||||||||||
де V = Vx = Vx′ |
(проекція |
вектора |
на |
вісь |
X |
збігається |
із |
проекцією |
того ж вектора |
на |
|||||||||||||||||
вісь X ′ ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Диференціювання другого й третього з рівнянь (40.1) приводить до такого результату |
|||||||||||||||||||||||||||
|
|
dy = |
dy′ |
= |
|
dy′ |
, |
тобто υ |
y |
= υ′ |
; |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
dt |
|
|
dt |
|
|
|
|
|
dt′ |
|
|
|
|
|
y′ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
dz = |
dz′ |
= |
dz′ |
, тобто υ |
z |
= υ′ |
. |
|
|
|
(40.3) |
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
dt dt dt′ |
|
|
|
|
|
z′ |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Сукупність рівнянь (40.2) і (40.3) можна подати одним векторним рівнянням |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
r |
|
|
r |
|
|
. |
|
|
|
|
|
|
|
(40.4) |
||||
|
|
|
|
|
|
|
|
|
υ = υ′ +V |
|
|
|
|
|
|
|
|||||||||||
Це рівняння можна розглядати або як формулу перетворення швидкості частинки від системи K′ до системи K або як закон додавання швидкостей в ньютонівській механіці:
швидкість частинки відносно нерухомої системи K дорівнює сумі швидкості частинки відносно рухомої системи K′ й швидкості системи K′ відносно системи K .
3 Диференціювання за часом рівняння (40.4) приводить до рівності |
|
|
|
a = a′ |
(40.5) |
(V = const |
, тому dV / dt = 0 ). Таким чином, прискорення частинки відносно систем K і K′ |
|
однакові. |
Сила F , що діє на частинку в системі K , збігається з силою |
F′, що діє на |
частинку в системі K′ : |
|
|
|
F = F′. |
(40.6) |
Це випливає з того, що сила залежить від відстаней між даною частинкою й частинками, що взаємодіють з нею (і може бути від відносних швидкостей частинок). А ці відносні відстані (й відносні швидкості) в ньютонівській механіці вважаються однаковими у всіх інерціальних системах відліку. Маса також має однакове числове значення у всіх системах відліку.
Зі сказаного випливає, що якщо в системі K виконується рівність
r
ma = F ,
то в системі K′ буде виконуватися рівність
′r′ = ′. m a F
Системи K й K′ були взяті зовсім довільно. Тому отриманий результат означає, що закони механіки однаково формулюються для всіх інерціальних систем відліку. Це твердження називається принципом відносності Галілея.
4 Галілей перший звернув увагу на те, що ніякими механічними дослідами, виконаними в межах даної інерціальної системи відліку, неможливо встановити, чи
65
перебуває вона в стані спокою або в стані рівномірного прямолінійного руху. Він писав, що в закритій каюті корабля, який рівномірно рухається, мухи летять із однаковою швидкістю в усіх напрямках; відстань, на яке ви стрибнете, не залежить від напрямку стрибка; краплі з отвору в дні підвішеного відерця будуть падати так само, як вони падали, коли корабель був нерухомим. Імовірно, кожному доводилося, розглядаючи з вікна вагона поїзд, який стоїть на сусідньому шляху, відчути, начебто вагон, у якому ви перебуваєте, почав рухатися, у той час як насправді рушав з місця сусідній поїзд. Усі перелічені процеси є проявом принципу відносності.
Інваріантними величинами називають величини, які мають одне й те саме числове значення у всіх системах відліку (латинське слово invariantis означає «незмінний»). Прикладами таких величин можуть служити маса, електричний заряд та ін.
Інваріантними рівняннями відносно перетворення координат і часу при переході від однієї інерціальної системи відліку до іншої називаються рівняння, вигляд яких не змінюється при такому переході. Самі величини, що входять у рівняння, можуть при переході до іншої системи відліку змінюватись, однак формули, що виражають зв'язок між величинами, залишаються незмінними. Як приклад можна навести рівняння теореми про кінетичну енергію
Ek,2 − Ek ,1 = A
(збільшення кінетичної енергії тіла дорівнює виконаній над ним роботі). Ця рівність є справедливою у всіх інерціальних системах відліку, у той час як значення Ek,2 − Ek ,1 й A у
різних системах різні.
Користуючись поняттям інваріантності, принцип відносності Галілея можна сформулювати таким чином: рівняння механіки інваріантні відносно перетворень Галілея.
§ 41 Постулати спеціальної теорії відносності. Відносність одночасності [4,7]
1 У другій половині XIX століття Д.Максвелл створив теорію електромагнітного поля, яку сформулював у вигляді 4 рівнянь (рівняння Максвелла), які описували основні закономірності електромагнітних явищ. Один із наслідків цієї теорії полягає у тому, що електромагнітні поля можуть поширюватися у вакуумі у вигляді електромагнітних хвиль.
Причому швидкість цих хвиль, як випливало з розрахунків, була близькою до швидкості світла. Це дало підставу Д. Максвеллу зробити відкриття: світло – електромагнітне збурення яке поширюється у вигляді електромагнітних хвиль.
Однак рівняння Максвелла виявилися неінваріантними по відношенню до перетворень Галілея. Тобто при переході від однієї інерціальної системи відліку до іншої з застосуванням перетворень Галілея вигляд рівнянь змінювався. Це означало, що закони електромагнетизму змінюються при переході від однієї інерціальної системи відліку до іншої, що з фізичної точки зору не є вірним. Окрім цього, з теорії електромагнітного поля Максвелла випливало, що швидкість світла у вакуумі є сталою величиною, тобто не залежить від системи відліку. А це суперечить закону додавання швидкостей у ньютонівській механіці.
Де помилка? У теорії Максвелла? Чи в перетвореннях Галілея? На це питання повинен був дати відповідь експеримент. У першу чергу перевірялася «більш молода» теорія Максвелла. Вимірювалася швидкість світла в різних системах відліку. Експерименти показали: швидкість світла в вакуумі у різних системах відліку має одне й теж значення. Тобто теорія електромагнітного поля Максвелла є вірною.
Вирішення проблеми було знайдено А. Ейнштейном. У 1905 р. А. Ейнштейн створив спеціальну теорію відносності (СТВ), яка являє собою фізичну теорію простору й часу. В основі цієї теорії лежать два постулати: принцип відносності Ейнштейна й принцип інваріантності швидкості світла.
Ейнштейн поширив механічний принцип відносності Галілея на всі без винятку фізичні явища: всі закони природи однаково формулюються для всіх інерціальних систем
66
відліку. Також Ейнштейн показав, що перетворення Галілея потрібно замінити більше загальними перетвореннями Лоренца. Відповідно до цього принцип відносності Ейнштейна можна сформулювати у вигляді: рівняння, що виражають закони природи,
інваріантні відносно перетворень Лоренца.
Принцип інваріантності швидкості світла стверджує, що швидкість світла у вакуумі не залежить від руху джерел світла і є однаковою у всіх інерціальних системах відліку.
Незалежність швидкості світла від руху джерела можна було б не висувати як самостійний постулат, якщо із самого початку прийняти електромагнітну теорію світла. Однак таку фундаментальну теорію про простір та час, якою є теорія відносності, краще будувати, не пов'язуючи її з ніякими уявленнями про природу й механізми фізичних явищ.
2 У ньютонівській механіці одночасність вважається абсолютною. Тобто, коли в одній системі відліку дві події відбулись одночасно, то і в інших системах ці події також будуть одночасними. У спеціальній теорії відносності одночасність стає відносною. Тобто, якщо в одній системі відліку дві події є одночасними, то в іншій системі вони не обов’язково будуть
одночасними. Покажемо це на прикладі. |
|
|
|
|||||||||
|
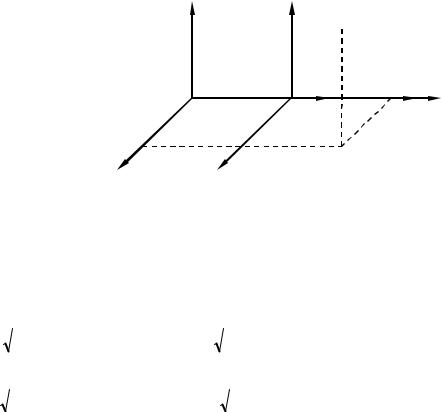
Розглянемо |
поїзд, |
який |
K |
K′ |
V |
O′ |
|
||||
рухається |
по |
поверхні |
Землі |
|
||||||||
рівномірно |
й |
прямолінійно зі |
|
|
2 |
|
1 |
|||||
швидкістю |
|
V |
(рис. 41.1). |
|
|
|
||||||
Візьмемо його за систему K′ , |
|
|
|
|
X |
|||||||
що |
рухається. |
Нерухомою |
|
|
|
O |
||||||
|
|
|
|
|||||||||
системою |
K |
будемо |
вважати |
Рисунок 41.1 – Поїзд (система |
K′ ) рухається відносно |
|||||||
платформу, повз яку проходить |
||||||||||||
платформи |
(система |
K ) зі |
швидкістю V . Світо |
|||||||||
поїзд. Нехай із середини поїзда |
||||||||||||
випромінюється з точки O′ , коли вона співпадає з точкою |
||||||||||||
O′ (рис. 41.1) |
випускається в |
|||||||||||
O . |
Пунктирною лінією показано положення поїзда в |
|||||||||||
обох |
напрямках |
світловий |
||||||||||
деякий момент часу після спалаху світла |
||||||||||||
сигнал, (відбувається |
спалах |
|||||||||||
|
|
|
|
|
||||||||
світла). У будь-який інерціальній системі відліку світло поширюється у всіх напрямках з однаковою швидкістю c . Тому пасажир, який їде у поїзді і в якому голова 1 і хвіст 2 поїзда нерухомі, відзначить, що сигнал досяг голови 1 й хвоста 2 поїзда одночасно. З іншого боку черговий станції, який знаходиться на платформі (в системі K ), відзначить, що сигнал який випущено з точки O і має швидкість c досяг хвоста 2 поїзда раніше, ніж голови 1. Це пов’язано з тим, що для чергового, повз який проходить поїзд, точки 1 й 2 рухаються. Точку 1 сигналу доводиться наздоганяти, а точка 2 рухається назустріч світлу. Тому сигнал приходить в точку 2 раніше ніж в точку 1. Тобто в системі K світло досягне кінців поїзда в різні моменти часу, неодночасно.
Таким чином, одночасність подій є відносною, вона залежить від системи відліку відносно якої розглядаються ці події.
3 З розглянутого приклада випливає, що в різних системах відліку час тече неоднаково. Простір і час втрачають відокремленість, незалежність один від одного, як це було у ньютонівській механіці. Як у СТВ визначають час? В якому випадку події слід вважати одночасними?
У спеціальній теорії відносності вимірювання часу проводять у такий спосіб. В кожній точці простору розміщують годинник. Вимірювання часу в даній точці простору проводять лише за годинником, який розміщено в цій точці простору. Для того щоб усі годинники показували однаковий час, потрібно провести їх синхронізацію. Ейнштейн запропонував спосіб синхронізації, який базується на другому постулаті СТВ. Сутність синхронізації така. Розглянемо два годинники, які розміщено в точках A й B . У середині відрізка AB зробимо світловий спалах. У момент приходу світла від спалаху до годинників A й B виставимо у них однаковий час. Тоді годинники будуть синхронізованими. Інші годинники синхронізуються аналогічно.
67
Таким чином, у СТВ використовуємо просторово-часову систему відліку з єдиним часом, у якій годинники синхронізовані між собою за правилом Ейнштейна. Дві просторово розділених події будемо називати одночасними, коли годинники, що знаходяться у точках, де відбулись ці події, показують один і той же час.
§ 42 Перетворення Лоренца [4]
1 Розглянемо |
інерціальні |
||
системи відліку K й K′ , які |
|||
показані на рис. 42.1. Осі |
X |
та X ′ |
|
збігаються між собою, |
Y |
та |
Y ′ , а |
також Z Z′ є паралельні одна одній. |
|||
Візьмемо, що система |
K′ |
рухається |
|
Y |
Y ′ |
K |
K′ |
O |
O′ V |
зі швидкістю V відносно нерухомої |
|
||||
системи K . Припустимо, |
що в |
|
|||
деякий момент часу в деякій точці |
Z |
||||
простору P |
відбувається |
деяка |
|||
|
|||||
подія. У |
системі |
K |
воно |
|
|
характеризується значеннями координат і часу
Z ′
Рисунок 42.1 x, y, z,t , а в системі
 P
P
X X ′
K′ – значеннями
координат і часу x′, y′, z′,t′ . Знайдемо формули, що позв'язують нештриховані значення зі
штрихованими.
Для розв’язання цієї задачі потрібно використати однорідність часу і простору, другий постулат СТВ. Шукані формули отримали назву перетворень Лоренца і мають такий вигляд
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
|
|
x′ +Vt′ |
|
, y = y′, z = z′, t = |
t′ + (V / c2 )x′ |
, |
|
(42.1) |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1− (V / c)2 |
|
1− (V / c)2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x′ = |
|
|
|
x −Vt |
|
, y′ = y, z′ = z, t′ = |
t − (V / c2 )x |
|
|
. |
(42.2) |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
1− (V / c)2 |
|
|
1− (V / c)2 |
|||||||||||||
|
|
|
|
|
|
|
||||||||||
У цих формулах c є швидкістю світла. Формули (42.1) описують перехід від системи K′ до системи K , а формули (42.2) – перехід від системи K до системи K′ . Внаслідок рівноправності систем перетворення (42.1) і (42.2) відрізняються лише знаком перед V . Ця
відмінність обумовлена тим, що система K′ рухається відносно системи K зі швидкістю V ,
у той час як система K рухається відносно системи K′ зі швидкістю ( −V ).
У перетвореннях Лоренца «перемішані» координати й час. Наприклад, час t у системі K визначається не тільки часом t′ у системі K′ , але також і координатою x′ . У цьому проявляється взаємозв'язок простору й часу.
2 Проведемо дослідження формул перетворень Лоренца у граничних випадках.
Розглянемо випадок, коли швидкості є набагато меншими за швидкість світла c . Тоді можна вважати, що c → ∞ . Коли ми підставимо c ≈ ∞ , наприклад, в (42.1), то отримаємо
x = x′ +Vt , y = y′ , z = z′ , t = t′ . |
(42.3) |
А формули (42.3) як відомо є формулами перетворень Галілея. Таким чином, у випадку, коли c → ∞ перетворення Лоренца переходять у перетворення Галілея.
Розглянемо випадок, коли V > c . Тоді вирази для x, t, x′ й t′ у формулах (42.1) і (42.2) стають уявними. Це відповідає тому факту, що рух зі швидкістю, яка перевищує швидкість світла c , є неможливим.
68
§ 43 Перетворення швидкостей у спеціальній теорії відносності [4]
1 Знайдемо |
зв’язок |
між |
|
|
|
Y |
|
|
|
|
|
Y ¢ |
|
r |
|||||
швидкістю |
частинки |
υ, що |
|
|
|
|
|
|
|
|
|
|
|
u |
|||||
виміряна в |
системі |
відліку K , та |
|
|
|
|
|
K |
K¢ |
|
|||||||||
швидкістю тієї самої частинки υ′ , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
що виміряна в системі відліку |
K′ . |
|
|
|
|
|
|
|
|
|
|
r |
X X ¢ |
||||||
Вважаємо, |
що |
система |
K′ |
|
|
|
O |
|
|
|
|
|
O¢ |
V |
|||||
рухається зі швидкістю V |
відносно |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
нерухомої |
системи |
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
||||
(див. рис. 43.1). |
|
|
υ |
Z |
|
|
Z ¢ |
|
|
||||||||||
Компоненти |
швидкості |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
Рисунок 43.1 |
|
||||||||||
частинки в системі |
K визначаються |
|
|
|
|
|
|
|
|
|
|||||||||
виразами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ux = |
dx |
, uy = |
dy |
|
, uz |
= |
dz |
. |
|
|
(43.1) |
||||
|
|
|
|
dt |
dt |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|||||||
У системі K′ компоненти швидкості υ′ |
тієї ж частинки дорівнюють |
|
|
||||||||||||||||
|
|
|
u¢x′ = |
dx′ |
|
, u¢y′ = |
dy′ |
, |
u¢z′ = |
dz′ |
. |
|
(43.2) |
||||||
|
|
|
dt¢ |
dt¢ |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
dt¢ |
|
|
|||||||
Знайдемо формули, що позв'язують нештриховані компоненти швидкості зі штрихованими. Для цього скористуємося перетвореннями Лоренца. Із цих формул отримуємо, що
|
¢ |
+V ×dt |
¢ |
¢ |
¢ |
dt |
¢ |
+ (V / c |
2 |
)dx |
¢ |
|
|||
|
dx |
|
|
|
|
|
|||||||||
dx = |
|
|
|
|
|
, dy = dy , |
dz = dz , dt = |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
1- (V / c)2 |
|
|
1- (V / c)2 |
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||
Розділивши перше із цих рівностей на четверте, прийдемо до співвідношення
|
dx |
|
dx′ +V ×dt′ |
dx′ / dt′ +V |
|
|||||
|
|
= |
dt¢ + (V / c2 )dx¢ |
= |
|
(V / c2 )dx¢ / dt¢ |
, |
|||
|
dt |
1+ |
||||||||
яке з урахуванням (43.1) і (43.2) |
можна подати у вигляді |
|
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
u′x′ +V |
|
|
|
||
|
|
|
|
ux = |
1+ (V / c2 )× u¢x′ |
. |
|
|||
(43.3)
(43.4)
Розділивши друге й третє з рівностей (43.3) на четверте, отримаємо ще два співвідношення:
|
|
|
|
|
|
|
|
|
|
|
uy = |
u¢y′ 1- (V / c)2 |
, |
uz = |
u¢z′ 1- (V / c)2 |
|
. |
(43.5) |
|||
1+Vu¢x′ / c2 |
1+Vu¢x′ / c2 |
|||||||||
|
|
|
|
|
||||||
Формули (43.4) та (43.5) і розв’язують поставлене завдання. Вони отримали назву формули перетворення або додавання швидкостей в СТВ.
За формулами (43.4) і (43.5) здійснюється перетворення швидкостей при переході від системи K′ до системи K . Використавши аналогічно як і вище перетворення Лоренца, легко
одержати формули |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u¢x′ = |
ux -V |
|
u¢y′ = |
uy 1- (V / c)2 |
, u¢z′ = |
uz 1- (V / c)2 |
|
|
|||
|
1- (V / c2 )× ux |
, |
|
|
|
|
|
, |
(43.6) |
|||
1-Vux / c2 |
1-Vux / c2 |
|||||||||||
за якими здійснюється перетворення швидкостей при переході від системи K до системи K′ . Формули (43.6) відрізняються від формул (43.4) і (43.5), як і слід було сподіватися, тільки знаком перед V . Формули (43.6) також називаються формулами перетворення або додавання швидкостей в СТВ.
69
2 Проведемо дослідження формул додавання швидкостей в СТВ у граничних випадках.
Розглянемо випадок, коли V << c . У цій ситуації вираз V / c << 1 і ним можна в формулах (43.4)–(43.6) знехтувати. У результаті отримуємо, наприклад, з (43.4) та (43.5)
ux = u′x′ +V , υy = υ′y′ , uz = u′z′
формули додавання швидкостей, за допомогою яких перетворюються швидкості в ньютонівській механіці. Таким чином, коли V << c формули додавання швидкостей у СТВ переходять у формули додавання швидкостей ньютонівської механіки.
Розглянемо випадок, коли частинка рухається паралельно осям X і X ′ в напрямку швидкості V (див. рис. 42.1). Тоді ux збігається з модулем швидкості частинки υ в системі
K , a u′x′ – з модулем швидкості υ′ в системі K′ , і формула (43.4) має вигляд |
|
||||||
|
|
u′ +V |
|
||||
|
u = |
1+ (V / c2 )× u¢ |
. |
|
(43.7) |
||
Швидкості υ, υ′ і V паралельні й направлені в одну й ту саму сторону. Отже, формула |
|||||||
(43.7) виражає закон додавання швидкостей. Якщо υ′ = c , то |
|
||||||
|
c +V |
(c +V )c |
|
||||
u = |
1+ (V / c2 )×c |
= |
|
= c . |
(43.8) |
||
(c +V ) |
|||||||
Таким чином, формула додавання швидкостей узгоджується с другим постулатом СТВ.
§ 44 Лоренцеве скорочення довжини [4]
1 Порівняємо довжину стержня в інерціальних системах відліку K й K′ (рис. 44.1). Припустимо, що стержень розміщено уздовж осей X і X ′ , які збігаються. У системі K′ стержень знаходиться у стані спокою. Відносно системи K він рухається зі швидкістю υ,
яка дорівнює швидкості V системи K′ відносно системи K .
Для визначення довжини стержня в системі K′ , де стержень знаходиться у стані спокою, потрібно прикласти до нього масштабну лінійку й визначити координату x1¢ одного
кінця стержня, а потім координату x¢2 іншого кінця. Різниця координат дасть довжину стержня l0 в системі K′ :
|
|
|
|
|
|
|
|
¢ |
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l0 = x2 |
- x1 . |
|
|
|
|
|
|
Довжину l0 , що виміряна в системі відліку, в |
|
Y |
Y ′ |
1 |
2 u |
||||||||||
якій |
тіло |
знаходиться |
у |
стані |
спокою, |
|
|
K |
K′ |
|
|
|
|||
|
|
|
|
|
|||||||||||
називають власною довжиною. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||
|
У |
системі |
K |
виміряти |
довжину |
|
|
|
|
|
|
|
|||
стержня складніше. Відносно системи K |
|
O |
O′ |
V |
|
X ′ X |
|||||||||
стержень |
рухається |
зі |
швидкістю |
υ, яка |
|
|
|
x1 |
x2 |
||||||
дорівнює |
швидкості |
V , |
з |
якою |
система |
|
|
|
|||||||
|
|
|
¢ |
¢ |
|||||||||||
рухається K′ відносно системи K . Оскільки |
|
|
|
||||||||||||
Z |
Z ′ |
x1 |
|
x2 |
|||||||||||
стержень рухається, потрібно визначити |
|
|
|
|
|||||||||||
координати його кінців |
x1 |
і |
x2 в один і той |
|
|
Рисунок 44.1 |
|
|
|||||||
же момент часу |
t1 = t2 |
= t . |
Тут t1 |
момент |
|
|
|
|
|
|
|
||||
часу, |
коли проводимо |
вимірювання координати x1 , |
t2 |
момент часу, коли |
проводимо |
||||||||||
вимірювання координати x2 . Різниця координат дасть довжину стержня l в системі K : l = x2 - x1 .
70
