

Знайдемо закон зміни заряду на конденсаторі та сили електричного струму від часу
при розрядженні конденсатора. |
|
q0 у початковий момент |
|
|
|
|
|
|
|
|
Якщо обкладки конденсатора з зарядом |
1 |
2 |
|
|
||||||
часу з'єднати провідником з опором |
R , то по провіднику пройде струм |
|
|
|
|
С |
|
|||
|
|
|
|
|
||||||
(див. рис. 112.1). Розглянемо ділянку кола 1–А–2 (див. рис. 112.1). Згідно |
|
q1 |
|
|
||||||
|
|
|||||||||
закону Ома електричний струм, що проходить по цій ділянці, дорівнює |
|
|
|
|
|
|
|
|||
I12 = ϕ1 − ϕ2 + E12 |
= ϕ1 − ϕ2 . |
|
(112.1) |
|
A |
|
|
|
|
|
R |
R |
|
|
|
|
|
|
|
|
|
Тут враховано, що на цій ділянці E = 0 ; ϕ та ϕ |
|
|
|
|
|
|
|
|
|
|
2 |
– потенціали відповідно |
|
R |
|
|
I12 |
||||
12 |
1 |
|
|
|
|
|
|
|
|
|
пластин 1 та 2 (див. рис. 112.1). З іншого боку, згідно з означенням ємності |
Рисунок 112.1 |
|||||||||
конденсатора |
|
|
|
|
|
|
|
|
|
|
C = q1 /(ϕ1 − ϕ2 ) , або ϕ1 − ϕ2 = q1 / C , |
|
|
|
(112.2) |
||||||
де q1 – заряд на пластині 1 конденсатора. Також зазначимо, що виходячи з означення сили електричного струму
I12 = dq / dt = −dq1 / dt , |
(112.3) |
де dq – кількість заряду, що пройшла через поперечний переріз провідника за час dt . Із
закону збереження електричного заряду випливає, |
що |
dq = −dq1 . Тобто коли сила струму |
||||||||||
I12 = dq / dt |
буде додатною, то заряд на пластині 1 конденсатора q1 буде зменшуватися |
|||||||||||
(тобто dq1 |
буде від’ємним), саме цим міркуванням обумовлений знак «–» у формулі (112.3). |
|||||||||||
Далі підставляємо (112.2) та (112.3) в (112.1) і отримуємо |
||||||||||||
|
|
|
|
− dq1 / dt = q1 /(RC) . |
|
|
||||||
Звідси, |
|
|
|
|
|
|
|
|
|
|
|
|
|
ò |
q1 |
dq' |
= −ò |
t |
dt' |
|
q |
= − |
t |
|
|
|
|
1 |
|
|
, або ln |
1 |
|
|
. |
|||
|
|
|
RC |
q0 |
RC |
|||||||
|
q0 |
q'1 |
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
З отриманих формул знаходимо, що заряд на конденсаторі змінюється з часом за законом
|
|
|
q1 = q0 exp(−t / τ) |
, |
(112.4) |
де q0 – початкове значення заряду конденсатора, а τ – стала: |
|
τ = RC , |
(112.5) |
що має розмірність часу. Вона називається часом релаксації. Через час τ заряд конденсатора зменшується в e раз. Тому τ за порядком величини дорівнює часу, протягом якого конденсатор розрядиться.
Використовуючи формулу (112.3) та (112.4), знаходимо закон зміни струму з часом:
I12 = −dq1 / dt = (q0 / τ) exp(−t / τ) = I0 exp(−t / τ) , |
(112.6) |
де I0 = q0 / τ = q0 /(RC) – початкове значення струму, тобто струм при t = 0 .
2 Знайдемо закон зміни заряду на конденсаторі та сили електричного струму від часу при зарядженні конденсатора.
Це завдання вирішується аналогічно до вищевикладеного. Нехай у коло конденсатора з опором R включено джерело струму з постійною електрорушійною силою E (див. рис. 112.2). Після замикання ключа K джерело збуджує струм, що заряджає конденсатор. Електричні заряди, що з’являються на обкладках конденсатора перешкоджають проходженню струму й зменшують його.
Розглянемо ділянку кола 1–А–2 (див. рис. 112.2). Згідно закону Ома електричний струм, що проходить по цій ділянці, дорівнює
181

|
|
|
|
|
|
I12 = ϕ1 − ϕ2 + E12 . |
(112.7) |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
q1 |
|
С |
|
Тут ϕ |
та ϕ |
2 |
– потенціали відповідно пластин 1 та 2 (рис. 112.2). |
|
K |
||||||||||
1 |
|
|
|
|
ϕ1 − ϕ2 |
|
|
|
|
|
|
|
|
||
Різницю потенціалів |
знаходимо аналогічно як і в (112.2) |
E |
|
|
|
||||||||||
ϕ1 − ϕ2 = q1 / C , де q1 |
– заряд на пластині 1 конденсатора. Стум на |
A |
|
|
|
||||||||||
опорі |
I12 |
і |
заряд |
|
на пластині 1 конденсатора |
q1 |
пов’язані |
|
|
|
|||||
|
R |
|
I12 |
|
|||||||||||
співвідношенням |
(112.3) |
I12 = dq / dt = −dq1 / dt . |
Також |
тут |
|
|
|||||||||
Рисунок 112.2 |
|
||||||||||||||
потрібно звернути увагу не те, що джерело струму у випадку |
|
||||||||||||||
рис. 112.2 |
включено |
так, що діє у напрямку, протилежному напрямку обходу |
контура |
||||||||||||
(напрямок обходу тут вибрано проти годинникової стрілки, напрямок сили струму збігається |
|||||||||||||||
з напрямком обходу). Тому у співвідношення (112.7) потрібно підставити ЕРС із знаком «–»: |
|||||||||||||||
E12 = −E . Також у (112.7) підставляємо різницю потенціалів і силу струму і отримуємо |
|
||||||||||||||
|
|
|
|
|
|
|
− Rdq1 / dt = q1 / C − E . |
|
|
|
|
|
|
||
Це рівняння можемо перетворити |
|
|
|
|
|
|
|
|
|||||||
dq1 |
+ |
q1 |
= |
E |
. |
(112.8) |
RC |
|
|||||
dt |
|
|
R |
|
||
Співвідношення (112.8) є неоднорідним диференціальним рівняння. Воно зводиться до однорідного, якщо його записати у вигляді
|
|
|
|
d(q1 − EC) |
+ |
(q1 − EC) |
= 0 . |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
dt |
|
|
|
RC |
|
|
|
|
|
Розділяючи змінні, отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
||
ò |
q1 |
d(q′ |
− EC) |
= −ò |
t |
dt' |
|
EC − q |
= − |
t |
|
|||
|
1 |
|
|
|
|
|
або ln |
|
1 |
|
. |
|||
|
(q′ − EC) |
|
RC |
|
EC |
RC |
||||||||
0 |
0 |
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Тут використали, що в момент часу t = 0 заряд на конденсаторі дорівнював нулю. Далі отримуємо шукану залежність заряду конденсатора від часу
|
|
|
q1 = EC(1− exp(−t / τ)) |
. |
(112.9) |
(112.10)
Знак «–» говорить про те, що струм у контурі (див. рис. 112.2) проходить у зворотному напрямку до обходу контуру. Струм максимальний у початковий момент і дорівнює E / R . Далі він зменшується за експонентним законом.
§ 113 Природа носіїв струму в металах. Дослід Рікке. Ідея Лоренца визначення відношення заряду до маси носія електричного струму в металах. Дослід Толмена і Стюарта [2]
1 Дослід Рікке. Для з'ясування |
природи |
|
Cu |
|
|
|
|
Al |
Cu |
|
|||
носіїв струму в металах був поставлений ряд |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
дослідів. Насамперед відзначимо дослід Рікке, |
|
|
|
|
|
|
|
|
|
|
|
|
|
здійснений у 1901 р. Рікке взяв три циліндри – два |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
мідних і один алюмінієвий – з |
ретельно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
відшліфованими торцями. Після зважування Рисунок 113.1 – Схема досліду Рікке циліндри були складені разом у послідовності: мідь – алюміній – мідь (див. рис. 113.1). Через такий складений провідник пропускався безупинно струм одного напрямку протягом року.
182
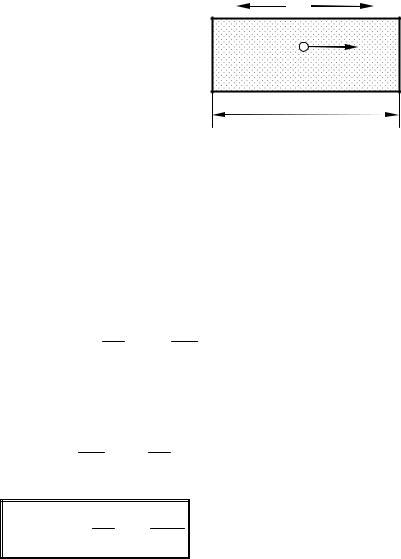
За увесь час через циліндри пройшов заряд, що дорівнював 3,5∙106 Кл. Зважування показало, |
||||||||||||||
що вага циліндрів не змінилася. При дослідженні торців циліндрів під мікроскопом не було |
||||||||||||||
виявлено проникнення одного металу в іншій. Результати досліду свідчили про те, що |
||||||||||||||
носіями струму в металах є не атоми, а якісь частинки, що входять до складу всіх металів. |
||||||||||||||
Такими частинками могли бути відкриті в 1897 р. Томсоном електрони. |
r |
|
||||||||||||
|
2 Ідея Лоренца визначення e/m. Щоб ототожнити |
r |
|
|
||||||||||
носії струму в металах з електронами, потрібно було |
a |
|
υ0 |
|
||||||||||
|
|
|
|
|||||||||||
визначити знак і числове значення питомого заряду носіїв. |
|
e′ |
- a |
|
||||||||||
Досліди, що були виконані із цією метою, ґрунтувалися на |
|
|
|
|||||||||||
таких міркуваннях. Якщо в металах є заряджені частинки, |
|
|
|
|
||||||||||
що здатні переміщуватися, то при гальмуванні металевого |
|
|
|
|
||||||||||
провідника ці частинки повинні якийсь час продовжувати |
|
|
l |
|
||||||||||
рухатися за інерцією, у результаті чого у провіднику |
|
Рисунок 113.2 |
|
|||||||||||
виникне імпульс струму й буде перенесений деякий заряд. |
|
|
||||||||||||
|
Нехай провідник рухається з початковою швидкістю |
υ0 (рис. 113.2). Почнемо |
||||||||||||
гальмувати його із прискоренням a . Продовжуючи рухатися |
за інерцією, носії струму |
|||||||||||||
отримують відносно провідника |
|
прискорення |
(−a) . У системі відліку, |
що пов’язана |
з |
|||||||||
провідником, на електрон діє сила інерції |
Fін |
|
r |
де |
m – |
маса носія струму. Fін |
є |
|||||||
= −ma , |
||||||||||||||
сторонньою силою. Напруженість поля сторонніх сил дорівнює |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
Eст = Fін / e′ = −ma / e′ , |
|
|
|
|
|||||||
де e′ |
–заряд носія струму. Таким чином, у колі виникає ЕРС |
|
|
|
|
|||||||||
|
|
|
2 |
r |
r |
2 |
|
r |
r |
mal |
|
|
|
|
|
|
|
ò |
ò |
ma |
|
|
|
|
|||||
|
E = |
Eстdl = − |
e′ |
dl = − |
e′ |
, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
де l |
– довжина провідника. У цьому випадку по провіднику пройде струм силою I = E / R , |
|||||||||||||
де R |
– опір провідника (струм |
I |
|
вважаємо додатним, |
коли струм проходить у напрямку |
|||||||||
руху провідника). Отже, за час dt |
через кожний перетин провідника пройде заряд |
|
||||||||||||
|
dq = Idt = − mal dt = − ml |
dυ . |
|
|
|
|
||||||||
|
|
|
|
|
e′R |
|
|
e′R |
|
|
|
|
|
|
Тут врахували, що a × dt = du. Заряд, що пройшов за увесь час гальмування, дорівнює |
|
|||||||||||||
|
|
|
|
|
0 |
ml |
|
mlυ0 |
|
|
|
|
||
|
q = òdq = − ò e′R dυ = e′R . |
|
|
(113.1) |
||||||||||
|
|
|
|
|
υ0 |
|
|
|
|
|
|
|
|
|
Заряд є додатним, коли він переноситься у напрямку руху провідника.
Таким чином, вимірявши l , υ0 і R , а також заряд q , що проходить по колу під час
гальмування провідника, можна знайти питомий заряд носіїв. Напрямок імпульсу струму дасть інформацію про знак носіїв.
3 Дослід Толмена і Стюарта. Кількісний результат був отриманий Толменом і Стюартом у 1916 р. Котушка із провідника довжиною 500 м приводилася в обертання, при якому лінійна швидкість витків становила 300 м/с. Потім котушка різко гальмувалася й за допомогою балістичного гальванометра вимірювався заряд, що проходив у колі за час гальмування. Обчислене за формулою (113.1) значення питомого заряду носіїв, було дуже близьким до e / m для електронів. Таким чином, було експериментально доведено, що носіями струму в металах є електрони.
4 Дослід показує, що струм у металах можна викликати вкрай малою різницею потенціалів. Це дає підставу вважати, що носії струму – електрони переміщуються в металі практично вільно. До того ж висновку приводять і результати досліду Толмена й Стюарта.
183
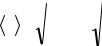
Існування в металах вільних електронів можна пояснити тим, що при утворенні кристалічної решітки від атомів металу від’єднуються слабкіше усього зв'язані (валентні) електрони, які стають «колективною» власністю усього металу. Якщо від кожного атома від’єднати по одному електрону, то концентрація вільних електронів (тобто їх число в одиниці об'єму) буде дорівнює кількості атомів в одиниці об'єму. Число атомів в одиниці об'єму дорівнює r/ m0 = r/(m / NA ) = rNA / m , де m0 – маса одного атому; ρ – густина металу;
μ– маса моля; NA – число Авогадро. Звідси знаходимо, що концентрації вільних електронів
уметалах приймають такі значення
n =1028 -1029 м–3. |
(113.2) |
§ 114 Якісні уявлення про електропровідність металів з точки зору класичної теорії. Закон Ома та Джоуля-Ленца з погляду класичної теорії електропровідності. Недоліки класичної теорії електропровідності [5]
1 Якісні уявлення про електропровідність металів. Виходячи з уявлення про вільні електрони, Друде створив класичну теорію електропровідності металів у 1900 р., яка потім була удосконалена Лоренцом. Друде припустив, що носії струму в металах – електрони поводяться подібно молекулам ідеального газу. У проміжках між зіткненнями вони рухаються під час відсутності поля вільно, пробігаючи в середньому деякий шлях λ . На відміну від молекул газу, пробіг яких визначається зіткненнями молекул одна з одною, електрони зіштовхуються переважно не між собою, а з іонами, що утворюють кристалічну решітку металу. Ці зіткнення приводять до встановлення теплової рівноваги між електронним газом і кристалічною решіткою.
Для оцінки середньої швидкості теплового руху електронів провідності в металах скористаємося формулою для середньої швидкості теплового руху молекули, поклавши температуру такою, що дорівнює 300 К:
u = |
|
8kT |
|
= |
|
8×1,38×10−23 ×300 |
»105 м / с . |
|
|
pm |
|
3,14×0,91×10−30 |
|
||||||
|
|
|
|
|
|
|
|||
У цій формулі m – маса електрона; k |
– стала Больцмана. |
|
|
||||||
Після включення електричного поля на хаотичний рух, який відбувається зі |
|||||||||
швидкістю < υ > , накладається |
впорядкований рух електронів з деякою |
середньою |
|||||||
швидкістю < u > . Величину цієї швидкості легко оцінити, виходячи з формули |
|
||||||||
|
|
|
|
|
|
|
j = ne < u > , |
|
(114.1) |
де n та e є відповідно концентрація та заряд електрона. Найбільша можлива густина електричного струму, коли провідник ще не перетворюється на рідину через виділення
великої кількості тепла, для міді дорівнює близько 107 А/м2. Якщо взяти для n значення 1029 м–3, то отримаємо
< u >= |
I |
= |
|
107 |
|
»10−3 |
м/с. |
|
en |
1,6×10−19 |
×1029 |
||||||
|
|
|
|
|||||
Таким чином, навіть при дуже великих густинах електричного струму середня
швидкість впорядкованого руху електронів < u > приблизно в 108 разів менше середньої швидкості теплового руху < υ > . Тому в обчисленнях модуль результуючої швидкості | υ + u | можна заміняти модулем теплового руху | υ |.
2 Закон Ома. Друде припускав, що електричне поле збільшує швидкість електрона і надає йому деяку додаткову енергію. Під час зіткнення електрона з іоном решітки набута ним за час пробігу додаткова енергія повністю передається іону. Далі електричне поле знову прискорює електрон, знову має місце зіткнення і т.д. Отримаємо закон Ома, виходячи з вище описаної моделі руху електрона в металі.
184

Якщо поле в металі є однорідним, то електрон рухається деякий час τ (час пробігу) з постійним прискоренням a = eE / m ( e та m є відповідно зарядом та масою електрона, E є напруженістю електричного поля) й за час пробігу τ швидкість упорядкованого руху досягає значення
umax = a ×t = |
eE |
t = |
eE |
|
l |
, |
(114.2) |
|
m |
m < u > |
|||||||
|
|
|
|
|||||
де λ – довжина вільного пробігу; < υ > – його результуюча швидкість, яка, як ми з’ясували вище, практично збігається з тепловою < υ > .
Швидкість u змінюється за час пробігу лінійно. Тому її середнє значення дорівнює
половині максимального: |
|
|
|
|
|
u = |
1 |
umax = |
eEl |
. |
|
2 |
2m < u > |
||||
|
|
|
Підставивши це значення середньої швидкості впорядкованого руху носіїв струму у формулу для густини електричного струму, отримаємо
j = ne u = |
ne2l |
E = sE |
, |
(114.3) |
|
2m < u > |
|||||
|
|
|
|
де n є концентрацією носіїв струму (вільних електронів у металі). Таким чином, ми прийшли до закону Ома в диференціальному вигляді. Більше того, виходячи з класичної теорії електропровідності металів, ми отримали вираз для провідності:
s = |
ne2l |
|
2m < u > . |
(114.4) |
Звідси випливає, якби електрони не мали зіткнень, довжина вільного пробігу, а отже, і провідність були б нескінченно великі. Таким чином, відповідно до класичних уявлень опір металів обумовлений зіткненнями електронів провідності з іонами кристалічної решітки.
3 Закон Джоуля-Ленца. Розглядаємо попередню модель руху електронів у провіднику. Знайдемо середнє значення додаткової кінетичної енергії електронів, що обумовлена дією електричного поля. Швидкість електронів дорівнює сумі швидкості теплового руху υ й швидкості впорядкованого руху u . Середнє значення квадрата результуючої швидкості дорівнює
r |
r |
r |
r r |
+ u2 |
= u2 + 2 uu cosa + u2 , |
(u + u)2 |
= u2 |
+ 2uu |
|||
де α – кут між векторами υ й u (усереднення виконується за усіма електронами). Швидкість υ хаотичного руху має з рівною ймовірністю найрізноманітніші напрямки. Тому всі значення cosα від –1 до +1 мають однакову ймовірність. Через цю причину середнє значення υu cosα дорівнює нулю. Таким чином,
(r r)2 2 2
u + u = u + u .
Звідси випливає, що середня кінетична енергія електронів складається з постійного доданка m < u2 > / 2 й додаткового доданка
 Dek
Dek  = 12 m
= 12 m u2
u2  ,
,
який обумовлений полем.
У момент перед зіткненням u має значення umax (див. формулу (114.2)) й додаткова кінетична енергія дорівнює
Dek = |
1 |
mumax2 |
= |
e2l2 |
E2 . |
(114.5) |
|
2 |
2m < u >2 |
||||||
|
|
|
|
|
|||
|
185 |
|
|
||||

Зіштовхнувшись із іоном, електрон, за припущенням, віддає йому (тобто решітці) всю отриману ним додаткову енергію. Кожний електрон має за секунду < υ > / λ зіткнень, передає щоразу решітці енергію (114.5). Тому в одиниці об'єму за одиницю часу буде виділятися кількість теплоти
|
Q = n |
< υ > ε |
k |
= |
ne2λ |
E2 = σE2 |
, |
(114.6) |
|||
|
|||||||||||
|
пит |
|
λ |
|
|
|
2m < υ > |
||||
|
|
|
|
|
|
|
|
|
|||
де σ є провідністю, формула для якої збігається з (114.3). Зазначимо, |
що закон Джоуля- |
||||||||||
Ленца в диференціальній формі має вигляд |
|
|
|
|
|
|
|
|
|||
|
Q |
|
= ρj2 |
= |
1 |
(σE)2 = σE2 . |
|
(114.7) |
|||
|
|
|
|
||||||||
|
пит |
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Порівнюючи (114.7) та (114.6) бачимо, що отримане співвідношення (114.6) є законом Джоуля-Ленца в диференціальному вигляді. Співвідношення для провідності σ , які отримані з закону Ома (114.3) та закону Джоуля-Ленца, збігаються між собою.
4 Недоліки класичної теорії електропровідності металів. Підбиваючи підсумок,
можна сказати, що класична теорія електропровідності змогла пояснити закони Ома й Джоуля-Ленца, а також дала якісне пояснення деяким іншим законам. Разом з тим ця теорія зустрілася з досить істотними утрудненнями.
З формули (114.4) випливає, що опір металів ρ = 1/ σ (тобто величина, зворотна до σ ) повинна зростати
ρ = 1/ σ = |
2m < υ > |
~< υ >= |
|
8kT |
|
~ |
|
|
|
T |
|||||||
ne2λ |
πm |
|||||||
|
|
|
|
|
|
як корінь квадратний з температури. Дійсно, для припущення про залежність величин n і λ від температури немає ніяких підстав. Швидкість же теплового руху пропорційна кореню з
температури 
 T . Цей висновок теорії суперечить дослідним даним, згідно яким електричний опір металів росте пропорційно першого ступеня температури T , тобто
T . Цей висновок теорії суперечить дослідним даним, згідно яким електричний опір металів росте пропорційно першого ступеня температури T , тобто
швидше, ніж 
 T .
T .
Як відомо, при низьких температурах у металах спостерігається відсутність опору
(явище надпровідності). Класична теорія електропровідності явище надпровідності не змогла пояснити.
Нарешті, класична теорія не змогла пояснити самого головного – чому електрони в металах виявляються вільними.
Недоліки класичної теорії електропровідності пов’язані з тим, що об’єкти мікросвіту, якими є електрони в металах, описуються квантовою, а не класичною
механікою.
§ 115 Електричний струм у газах. Несамостійний газовий розряд. Густина струму у випадку слабих та сильних електричних полів [5]
1 Проходження електричного струму через гази називається газовим розрядом. Гази в нормальному стані є ізоляторами, носії струму в них відсутні. Лише при створенні особливих умов у газах можуть з'явитися носії струму (іони, електрони) і виникає електричний розряд.
Носії струму в газах можуть виникати в результаті зовнішніх впливів, не пов'язаних з наявністю електричного нуля. У цьому випадку говорять про несамостійний розряд газу.
Несамостійний розряд може бути викликаний нагріванням газу (термічна іонізація), впливом ультрафіолетових або рентгенівських променів, а також впливом випромінювання радіоактивних речовин.
186

Якщо ж носії струму виникають у результаті процесів, які обумовлені створеним у газі електричним полем, розряд називається самостійним. Далі в цьому параграфі будемо
розглядати властивості лише несамостійного розряду. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 Несамостійний газовий розряд. |
Нехай |
|
газ, |
що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
знаходиться між електродами (рис. 115.1), знаходиться під дією |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
постійного за інтенсивністю однорідного впливу, наприклад |
|
+ |
|
|
+ |
|
|
|
– |
|
|||||||||||
рентгенівських променів. Завдяки цьому від деяких молекул |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
- |
|
|
|
|
|
|
|
||||||||||
газу будуть відриватись електрони, у результаті чого виникнуть |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
вільні електрони й додатні іони. Умовно будемо називати |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
електрони від’ємними іонами. Додатні іони будемо вважати |
|
|
|
|
|
l |
|
|
|
|
|
|
|||||||||
однозарядними (тобто такими, що мають заряд |
+ e |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Позначимо число пар іонів, які виникають за секунду в одиниці |
|
|
|
|
|
|
|
G |
|
|
|
||||||||||
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
об'єму, через ni . |
|
|
|
|
|
|
|
Рисунок |
115.1 |
|
|
– Схема |
|||||||||
|
Одночасно з процесом іонізації має місце рекомбінація |
|
|
||||||||||||||||||
іонів, тобто возз'єднання при зустрічі електрона й додатного |
приладу |
|
для |
|
|
вивчення |
|||||||||||||||
іона. Імовірність зустрічі двох різнойменних іонів пропорційна |
несамостійного |
|
|
газового |
|||||||||||||||||
як числу додатних, так і числу від’ємних іонів. Тому число пар |
розряду. Площа електро- |
||||||||||||||||||||
іонів |
& |
|
одиниці об'єму, є |
дів S , об'єм простору між |
|||||||||||||||||
nr , які рекомбінують за секунду в |
електродами дорівнює Sl |
||||||||||||||||||||
пропорційним квадрату числа n наявних в одиниці об'єму пар |
|||||||||||||||||||||
іонів: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
= rn |
2 |
, |
|
|
|
|
|
|
|
|
|
|
(115.1) |
|||||
|
|
nr |
|
|
|
|
|
|
|
|
|
|
|
||||||||
де r |
коефіцієнт пропорційності. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тому |
У стані рівноваги число іонів, які виникають, дорівнює числу іонів, які рекомбінують. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
& |
& |
= rn |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni |
= nr або ni |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Звідси отримуємо величину рівноважної концентрації іонів (тобто число пар іонів в одиниці об'єму):
n = |
& |
(115.2) |
ni / r . |
Якщо подати напругу на електроди, зменшення іонів буде відбуватися не тільки внаслідок рекомбінації, але й за рахунок відбирання іонів електродами. Нехай з одиниці об'єму відбирається електродами кожну секунду n& j пар іонів. Нейтралізація на електродах
однієї пари іонів супроводжується переносом по електричному колу заряду e . Отже, сила струму в колі
I = dqdt = en& j Sl ,
де S ×l – об'єм простору між електродами. Використаємо, що густина електричного струму
пов’язана зі струмом співвідношенням j = I / S , і знаходимо |
(115.3) |
|||||
|
nj = j / el , |
|||||
& |
|
|
|
|
|
|
де l – відстань між електродами. |
|
|
|
|
|
|
При наявності струму умова рівноваги набуває вигляд |
|
|||||
|
ni |
= nr + nj . |
|
|||
& |
|
& |
& |
|
|
|
Підстановка виразів (115.1) і (115.3) приводить до співвідношення |
|
|||||
|
|
|
|
|
|
|
|
& |
|
2 |
+ j / el |
. |
(115.4) |
|
ni = rn |
|
||||
187
Як відомо, густина електричного струму для носіїв електричного струму одного типу визначається виразом
= × × r j n e u ,
де n – концентрація; e – електричний заряд; u – середня швидкість впорядкованого носіїв заряду. Зрозуміло, що середня швидкість впорядкованого руху буде тим більше, чим буде більшою напруженість електричного поля, тобто
r =
u u0 E ,
де коефіцієнт пропорційності u0 називають рухливістю носіїв електричного струму. Тоді густина електричного струму буде дорівнювати
j = n ×e ×u0 × E .
Якщо врахувати, що в газі є додатні (їх рухливість u0+ ) та від’ємні носії (їх рухливість u0− )
електричного струму, то модуль загального електричного струму буде визначатися співвідношенням
j = en(u0+ + u0− )E . |
(115.5) |
Розглянемо два граничні випадки – випадок слабких та випадок сильних електричних
полів.
У випадку слабких полів густина струму буде дуже малою. Тому другим доданком у правій частині рівності (115.4) можна знехтувати порівняно з першим і визначати концентрацію іонів за формулою (115.2). Підстановка цього виразу в (115.5) дає, що

 j = e
j = e
 n&i / r (u0+ + u0− )E = sE
n&i / r (u0+ + u0− )E = sE 
 .
.
Коефіцієнт σ не залежить від E . Отже, у випадку слабких полів несамостійний газовий
розряд описується законом Ома.
У випадку сильних полів практично всі іони будуть досягати електродів, не
встигнувши рекомбінувати. Тому в рівності (115.4) можна знехтувати доданком rn2 . У результаті отримаємо формулу
|
|
|
|
|
|
, |
|
|
(115.6) |
|
|
|
|
|
j = enil |
|
|
||
|
|
|
|
|
& |
|
|
|
|
відповідно до якої у випадку сильного поля густина електричного струму |
j не залежить |
||||||||
від напруженості електричного поля E . Ця густина струму формується усіма іонами, що |
|||||||||
|
|
|
|
|
|
|
|
|
& |
створюються іонізатором за одиницю часу, і є максимальною при даних значеннях ni і l . Її |
|||||||||
називають густиною струму насичення |
jнас . |
|
|
|
|||||
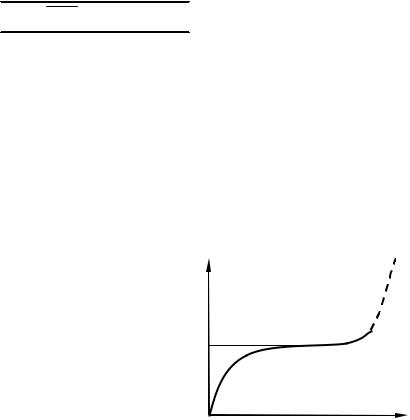
При проміжних |
значеннях напруженості E |
j |
|
|
|||||
відбувається плавний перехід від лінійної залежності |
|
|
|||||||
|
|
|
|||||||
j від E до насичення, коли j |
перестає залежати від |
|
|
|
|||||
E (рис. 115.2). При |
подальшому |
|
збільшенні |
|
|
|
|||
напруженості |
електричного |
поля |
починається |
jнас |
|
|
|||
стрімке зростання електричного струму (штрихова |
|
|
|
||||||
лінія). Це пояснюється тим, що, починаючи з деякого |
|
|
E |
||||||
значення E , |
електрони |
(рухливість, яких набагато |
|
|
|||||
вища за рухливість додатних іонів) встигають за час |
Рисунок 115.2 – Залежність густини |
||||||||
вільного пробігу отримати енергію, достатню для |
|||||||||
того, щоб, зіштовхнувшись із молекулою, іонізувати |
струму |
при |
несамостійному |
||||||
її. Електрони, що виникають при іонізації, |
газовому |
розряді від напруженості |
|||||||
розганяються, |
і у свою чергу викликають іонізацію. |
електричного поля |
|
||||||
У результаті відбувається лавиноподібне розмноження носіїв струму й різке зростання розрядного струму.
188
§ 116 Процеси, що приводять до виникнення носіїв струму при самостійному газовому розряді. Самостійний газовий розряд [5]
Як відомо, самостійним називають такі розряди, коли носії струму у газі виникають
урезультаті процесів, що обумовлені створеним у ньому електричним полем .
1Процеси, що приводять до виникнення носіїв струму при самостійному газовому розряді. Залежно від умов, у яких проходить самостійний газовий розряд, він може
набирати різноманітної форми. Перш ніж приступити до їх опису, розглянемо процеси, які приводять до виникнення носіїв струму при самостійному газовому розряді.
Іонізація ударом. Енергія молекул (так само як і атомів) кантується. Це означає, що вона може набувати лише дискретні (тобто розділені скінченними проміжками) значення, які називають рівнями енергії. Стан з найменшою енергією називається основним, інші стани називаються збудженими. При зіткненні електрона з молекулою вона може перейти з основного стану в збуджений. У цьому стані молекула, як правило, перебуває час порядку 10–8 с, після чого переходить в основний стан, випромінюючи надлишок енергії у вигляді кванта світла – фотона. Ці процеси викликають світіння газу при розряді. При досить великій енергії електрона, що налітає, молекула може бути іонізована, тобто, втративши один або кілька електронів, перетворитися в додатний іон.
Фотоіонізація. Електромагнітне випромінювання (зокрема, світло) складається із квазичастинок – фотонів, енергія яких дорівнює hν ( h – стала Планка, ν – частота випромінювання). Поглинання фотона молекулою приводить до її збудження або іонізації (яка в цьому випадку називається фотоіонізацією). Енергії фотона видимого світла недостатньо для відриву електрона від молекули. Енергію, достатньої для фотоіонізації, мають фотони ультрафіолетового випромінювання.
Емісія електронів поверхнею електродів. Електрони провідності не можуть самовільно залишати метал у помітній кількості. Це пояснюється тим, що метал представляє для електронів потенційну яму, яка має потенціальний бар'єр на границі металу. Сили, що обумовлюють цей бар'єр, мають наступне походження. Випадкове видалення електрона від зовнішнього шару додатних іонів приводить до виникнення у тому місці, що покинув електрон, надлишкового додатного заряду. Кулонівська взаємодія із цим зарядом змушує електрон, швидкість якого не дуже велика, повернутися назад. Таким чином, окремі електрони увесь час залишають поверхню металу, віддаляються від нього на декілька міжатомних відстаней і вертаються назад. У результаті метал виявляється оточеною тонкою хмарою електронів. Ця хмара утворює разом із зовнішнім шаром іонів подвійний електричний шар. Сили, що діють на електрон у такому шарі, спрямовані усередину металу. Вони й створюють потенційний бар'єр.
Найменша енергія, яку потрібно передати електрону для того, щоб видалити його із твердого або рідкого тіла у вакуум, називається роботою виходу Aвuх . Робота виходу дуже
чутлива до стану поверхні металу, зокрема до її чистоти. Підібравши покриття поверхні, можна сильно знизити роботу виходу. Наприклад, нанесення на поверхню вольфраму шару окисла лужного металу (Са, Sr, Ba) знижує роботу виходу з 4,5 еВ (для чистого вольфраму)
до 1,5 – 2еВ.
Внаслідок розподілу за енергіями завжди є деяка кількість електронів, енергія яких достатня для того, щоб перебороти потенційний бар'єр і вийти з металу назовні. При кімнатній температурі число таких електронів мале. При підвищенні температури кількість електронів, що вилітають із металу, різко зростає й стає цілком помітною. Випромінювання електронів нагрітими твердими або рідкими тілами називається термоелектронною емісією.
Вторинною електронною емісією називається випромінювання електронів поверхнею твердого або рідкого тіла при бомбардуванні її електронами або іонами. Відношення числа випромінених (вторинних) електронів до числа частинок, що викликали
189
емісію, називається коефіцієнтом вторинної емісії. У випадку бомбардування поверхні металу електронами значення цього коефіцієнта знаходиться у межах від 0,5 до 1,8.
Автоелектронною (або холодною) емісією називається випромінювання електронів поверхнею металів, що відбувається у випадку, коли поблизу поверхні створюється електричне поле дуже великої напруженості (порядку 108 В/м). Це явище називається також
вириванням електронів електричним полем.
2 Самостійний газовий розряд. Розглянемо декілька видів самостійного розряду. Тліючий розряд. Цей розряд виникає при низьких тисках. Його можна спостерігати в
скляній трубці з впаяними плоскими металевими електродами (рис. 115.3), подавши на електроди напругу порядку 1000 В. При атмосферному тиску струм у трубці практично відсутній. Якщо знижувати тиск, то приблизно при 50 мм рт. ст. виникає розряд у вигляді звивистого тонкого шнура, який світиться. Коли знижувати тиск далі, то шнур товщає й приблизно при 5 мм рт.ст. заповнює весь перетин трубки – встановлюється тліючий розряд.
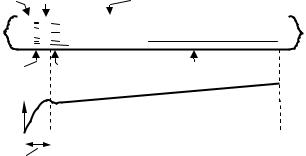
Основні частини тліючого розряду зазначені на рисунку 116.1. Біля катода знаходиться тонкий шар, що світиться, який називається катодною світною плівкою. Між катодом та світною плівкою знаходиться астонівський темний простір. З іншого боку від світної плівки розміщений катодний темний простір. Він світиться дуже слабо і за контрастом здається темним. Це катодний темний простір далі переходить в область, що слабо світиться, яку називають тліюче світіння. Усі перелічені вище шари утворюють катодну частину тліючого розряду.
Далі за тліючим світінням знаходиться темний проміжок – фарадеєвський темний простір. Межа між ними розмита. Уся інша частина трубки заповнена газом, який світиться;
її називають додатним стовпом.
Експериментальні виміри показали (див. нижню частину рисунка 116.1), що потенціал змінюється уздовж трубки нерівномірно. Майже усе падіння напруги приходиться на перші три ділянки розряду, до катодного темного простору включно. Цю частину напруги, яка прикладена до трубки, називають катодним падінням потенціалу. В області тліючого світіння потенціал не змінюється – тут напруженість електричного поля дорівнює нулю. Нарешті, у фарадеєвському темному просторі та додатному стовпі потенціал повільно росте.
Основні процеси, які необхідні для підтримки тліючого розряду, відбуваються у його катодній частини. Цих процесів два – вторинна електронна емісія з катода, яка викликана бомбардуванням його додатними іонами, і ударна іонізація електронами молекул газу. Ударна іонізація відбувається переважно в області катодного темного простору.
стовп |
Додатний |
|
Астонів − |
|
|
|
|
|
|
|
|
Темні |
|||||||
являє |
собою |
ський |
|
Катодний |
Фарадеєвський |
||||||||||||||
газорозрядну |
плазму. |
|
простори |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Він |
виконує |
роль |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
провідника, |
|
що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Катод |
|
|
|
|
|
|
|
|
|
Анод |
||||||||
з'єднує |
анод |
з |
|
|
|
Тліюче |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
Катодна |
|
|
|
|
|
|
|
|
|||||||||||
катодними частинами |
|
|
|
|
Додатний стовп |
Області, які |
|||||||||||||
|
|
|
світіння |
|
|||||||||||||||
розряду. |
Тому |
його |
плівка |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
світяться |
|||||||||||||
довжина |
може |
бути |
|
ϕ |
|
|
|
|
|
|
|
|
|||||||
довільною. |
Світіння |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
додатного стовпа має |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
різний |
|
колір |
для |
Катодне подання потенціалу |
|
|
|||||||||||||
різних |
газів |
(неонові |
Рисунок 116.1 – Тліючий розряд. Унизу показана зміна потенціалу |
||||||||||||||||
трубки дають червоне |
|||||||||||||||||||
уздовж газорозрядної трубки |
|
|
|
|
|
||||||||||||||
світіння, |
аргонові – |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
синьо-зелене й т.д.). Ця обставина використовується в газорозрядних трубках, з яких виготовляються світні написи й реклами. Ці написи являють собою додатний стовп тліючого розряду.
190
