Задание 7

Вычислить площадь фигуры, ограниченной линиями:

1.1 и осью ох

1.2 , у = 0, х = 0

1.3 и осью ОХ

1.4

1.5 и осью ОХ

1.6 , , х = −1, х = 0

1.7 и осью ОХ

1.8 и

1.9 и осью ОХ

1.10 y = 6x ­­­­­­­­−3x² и осью ОХ

1.11 и 1.21 y = x − y + 3, x + y −1= 0, y = 0

1.12 y = x ² и 1.22 2x − 3y + 6 = 0, y =0 и x = 3 1.13 и 1.23 и y = 3x −1

1.14 , , x = 0, x =2 1.24 x − y +2 = 0, y =0, x = −1, x = 2

1.15 , x =e , y =0 1.25 y ² = 4x, x = 1 и осью ОХ

1.16 , x =1, y = x − 1 1.26 и y = −3x

1.17 , , x = 0 , x = 1 1.27 x − y +3 =0 , x + y −1= 0, y = 0

1.18 , x = 2 1.28 x ² = 3y и y = x

1.19 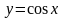, x = 0, x = 2π, y = 0 1.29 x ² + y ² = 9

1.20 y = , y = 2, x = 0 1.30

Контрольные вопросы

1. Что такое криволинейная трапеция?

2. Формула Ньютона-Лейбница

3. Графики элементарных функций.

Задание 8 (для всех вариантов)

1.Высота правильной треугольной пирамиды равна 6 см. Сторона ее основания - см. Вычислите длину ребра этой пирамиды.

2. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ проведено сечение плоскостью, содержащей прямую BD и вершину С_1. Угол между плоскостями сечения и основания равен 60°, AB=8см, ВС=6см. Вычислите площадь сечения.

3. Образующая конуса равна 18 см. Угол между образующей и плоскостью основания 60°. Найдите высоту и площадь основания конуса.

4. Площадь сечения шара плоскостью равна 36π см². Радиус шара, проведенный в точку окружности сечения, составляет с плоскостью сечения угол 45°. Найдите объем и площадь поверхности шара

Задание 9 (для всех вариантов)

1. Скорость движения точки v=(3t²-2t-3) м/с. Найдите путь, пройденный точкой за вторую секунду.

2. Скорость движения точки v=(36t-12t²) м/с. Найдите путь, пройденный точкой от начала движения до ее остановки.

3. Найдите длину дуги параболы y=x² между точками О(0,0) и А( )

4. Вычислить: sin α, если соs α= − 12/13, и П<α<3П/2

5. Вычислить cos α, если sin α = -4/5 и П<α<3П/2

9