Задание 1
1.Вычислить
определители второго порядка:
 ,
,
2.Вычислить
определители третьего порядка:
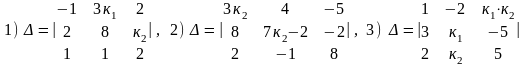
Вариант |
|
|
Вариант |
|
|
1 |
3 |
-2 |
16 |
4 |
-1 |
2 |
4 |
1 |
17 |
5 |
1 |
3 |
3 |
-4 |
18 |
2 |
0 |
4 |
2 |
1 |
19 |
-2 |
1 |
5 |
3 |
-3 |
20 |
2 |
-2 |
6 |
1 |
5 |
21 |
0 |
7 |
7 |
-2 |
3 |
22 |
-1 |
4 |
8 |
6 |
-2 |
23 |
-3 |
3 |
9 |
-6 |
1 |
24 |
-4 |
1 |
10 |
-5 |
1 |
25 |
0 |
8 |
11 |
-2 |
4 |
26 |
4 |
-2 |
12 |
1 |
3 |
27 |
-1 |
3 |
13 |
-3 |
2 |
28 |
2 |
-3 |
14 |
-4 |
-1 |
29 |
-2 |
5 |
15 |
-1 |
5 |
30 |
-5 |
-1 |
Контрольные вопросы:
Что называется определителем матрицы?
Как вычислить определитель второго порядка?
Какие способы вычисления определителя третьего порядка вам известны?
Перечислите свойства определителей.
Задание 2
Решить системы уравнений:
а) по формулам Крамера;
б) Методом Гаусса.

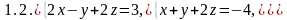

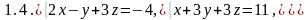













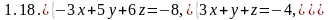









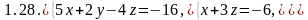


Задание 3
По координатам точек A, B и С для указанных векторов найти:
Координаты векторов
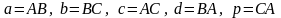
Модуль вектора

Скалярное произведение векторов а и b;
Векторное произведение векторов а и b
Смешанное произведение векторов а, b и с
Варианты |
Координаты точки А |
Координаты точки В |
Координаты точки С |
|
|
(-2, 1,3) |
(3, -6, 2) |
(-5, -3, -1) |
|
|
(1, 3, 6) |
(-3, 4, -5) |
(1, -7, 2) |
|
|
(7, 2, 1) |
(5, 1, -2) |
(-3, 4, 5) |
|
|
(3, 5, 4) |
(-2, 7, -5) |
(6, -2, 1) |
|
|
(5, 3, 2) |
(2, -5, 1) |
(-7, 4, -3) |
|
|
(11, 1, 2) |
(-3, 3, 4) |
(-4, -2, 7) |
|
|
(9, 5, 3) |
(-3, 2, 1) |
(4, -7, 4) |
|
|
(7, 2, 1) |
(3, -5, 6) |
(-4, 3, -4) |
|
|
(1, 2, 3) |
(-5, 3, -1) |
(-6, 4, 5) |
|
|
(-2, 5, 1) |
(3, 2, -7) |
(4, -3, 2) |
|
|
(3, 1, 2) |
(-4, 3, -1) |
(2, 3, 4) |
|
|
(3, -1, 2) |
(-2, 4, 1) |
(4, -5, - 1) |
|
|
(4, 5, 1) |
(1, 3, 1) |
(-3, -6, 7) |
|
|
(1, -3, 1) |
(-2, -4, 3) |
(0, -2, 3) |
|
|
(5, 7, -2) |
(-3, 1, 3) |
(1, -4, 6) |
|
|
(-l, 4, 3) |
(3, 2, -4) |
(-2, -7, 1) |
|
|
(5, 4, 1) |
(-3, 5, 2) |
(2, -1, 3) |
|
|
(2, -1, 4) |
(-3, 0, -2) |
(4, 5, -3) |
|
|
(-1, 1, 2) |
(2, -3, -5) |
(-6, 3, -1) |
|
|
(1, 3, 4) |
(-2, 5, 0) |
(3, -2, -4) |
|
|
(1, -1, 1) |
(-5, -3, 1) |
(2, -1, 0) |
|
|
(3, 1, 2) |
(-7, -2, -4) |
(-4, 0, 3) |
|
|
(-3, 0, 1) |
(2, 7, -3) |
(-4, 3, 5) |
|
|
(5, 1, 2) |
(-2, 1, -3) |
(4, -3, 5) |
|
|
(0, 2, -3) |
(4, -3, -2) |
(-5, -4, 0) |
|
|
(3, -1, 2) |
(-2, 3, 1) |
(4, -5, -3) |
|
|
(5, 3, 1) |
(-1, 2, -3) |
(3, -4, 2) |
|
|
(3, 1, -3) |
(-2, 4, 1) |
(1, -2, 5) |
|
|
(6, 1, -3) |
(-3, 2, 1) |
(-1, -3, 4) |
|
|
(4, 2, 3) |
(-3, 1, -8) |
(2, -4, 5) |
Контрольные вопросы
Что называется вектором?
Какие векторы называются коллинеарными?
Что называется координатами вектора?
Как найти координаты вектора, заданного двумя точками?
Как найти длину вектора, заданного своими координатами?
Запишите формулы деления отрезка в данном отношении.
7. Дать определение проекции вектора на ось и перечислить ее свойства.
8. Дать определение скалярного произведения векторов.
9. Дать определение векторного произведения векторов.
10. Дать определение смешанного произведения векторов.
Задание 4
Вершины пирамиды находятся в точках А, В, С и D. Вычислить:
а) площадь указанной грани;
б) объем пирамиды ABCD.
Ответы
Вариант |
Координаты вершины А |
Координаты вершины В |
Координаты вершины С |
Координаты вершины Д |
Грань а) |
1 |
A(3, 4, 5) |
В(1, 2, 1) |
С(-2, -3, 6) |
D(3, -6, -3) |
ACD |
2 |
А(-7, -5, 6) |
В(-2, 5, -3) |
С(3, -2, 4) |
D(l, 2, 2) |
BCD |
3 |
A(1, 3, 1) |
В(-1, 4, 6) |
С(-2, -3, 4) |
D(3, 4, -4) |
ACD |
4 |
А(2, 4, 1) |
В(-3, -2, 4) |
С(3, 5, -2) |
D(4, 2, -3) |
ABD |
5 |
A(-5, -3, -4) |
В(1, 4, 6) |
С(3, 2, -2) |
D(8, -2, 4) |
ACD |
6 |
A(3, 4, 2) |
В(-2, 3, -5) |
С(4, -3, 6) |
D(6, -5, 3) |
ABD |
7 |
A(-4, 6, 3) |
В(3, -5, 1) |
С(2, 6, -4) |
D(2, 4, -5) |
ACD |
8 |
A(7, 5, 8) |
В(-4, -5, 3) |
С(2, -3, 5) |
D(5, 1, -4) |
BCD |
9 |
A(3, -2, 6) |
В(-6, -2, 3) |
С(1, 1, -4) |
D(4, 6, -7) |
ABD |
10 |
A(-5, -4, -3) |
В(7, 3, -1) |
С(6, -2, 0) |
D(3, 2, -7) |
BCD |
11 |
A(3, -5, -2) |
В(-4, 2, 3) |
С(1, 5, 7) |
D(-2,-4, 5) |
ACD |
12 |
А(7, 4, 9) |
В(1, -2, -3) |
С(-5, -3, 0) |
D(1, -3, 4) |
ABD |
4 |
A(-4, -7, -3) |
В(-4, -5, 7) |
С(2, -3, 3) |
D(3, 2, 1) |
BCD |
14 |
А(-4, -5, -3) |
В(3, 1, 2) |
С(5, 7, -6) |
D(6, -1, 5) |
ACD |
15 |
A(5, 2, 4) |
В(-3, 5, -7) |
С(1, -5, 8) |
D(9, -3, 5) |
ABD |
16 |
A(-6, 4, 5) |
В(5, -7, 3) |
С(4, 2, -8) |
D(2, 8, -3) |
ACD |
17 |
A(5, 3, 6) |
В(-3, -4, 4) |
С(5, -6, 8) |
D(4, 0, -3) |
BCD |
18 |
A(5, -4, 4) |
В(-4, -6, 5) |
С(3, 2, -7) |
D(6, 2, -9) |
ABD |
19 |
A(-7, -6, -5) |
В(5, 1, -3) |
С(8, -4, 0) |
D(3, 4, -7) |
BCD |
20 |
A(7, -1, -2) |
В(1, 7, 8) |
С(3, 7, 9) |
D(-3, -5, 2) |
ACD |
21 |
A(5, 2, 7) |
В(7, -6, -9) |
С(-7, -6, 3) |
D(l, -5, 2) |
ABD |
22 |
A(-2, -5, -1) |
В(-6, -7, 9) |
С(4, -5, 1) |
D(2, 1, 4) |
BCD |
23 |
A(-6, -3, -5) |
В(5, 1, 7) |
C(3, 5, -1) |
D(4, -2, 9) |
ACD |
24 |
A(7, 4, 2) |
B(-5, 3, -9) |
C(1, -5, 3) |
D(7, -9, 1) |
AВD |
25 |
A(-8, 2, 7) |
B(3, -5, 9) |
С(2, 4, -6) |
D(4, 6, -5) |
AСD |
26 |
A(4, 3, 1) |
В(2, 7, 5) |
С(-4, -2, 4) |
D(2, -3, -5) |
ACD |
27 |
A(-9, -7, 4) |
B(-4, 3, -1) |
С(5, -4, 2) |
D(3, 4, 4) |
BCD |
28 |
A(3, 5, 3) |
В(-3, 2, 8) |
С(-3, -2, 6) |
D(7, 8, -2) |
ACD |
29 |
A(4, 2, 3) |
B(-5, -4, 2) |
С(5, 7, -4) |
D(6, 4, -7) |
ABD |
30 |
A(-4, -2, -3) |
В(2, 5, 7) |
С(6, 3, -1) |
D(6, -4, 1) |
ACD |
Контрольные вопросы
Как вычисляется скалярное произведение векторов, заданных своими координатами?
Как вычисляется векторное произведение векторов?
Что называется смешанным произведением векторов?
Какие векторы называются компланарными?