
Физика твёрдого тела / 2сем / [3] Проценко І.Ю., Шумакова Н.І., Овчаренко Ю.М. Фізика твердого тіла Навчальний посібник. – Суми Видавництво
.pdf
У випадку кубічної та інших прямокутних решіток
k1 = 2aπ, k2 = 2bπ, k3 = 2cπ ,
тобто вектори оберненої решітки визначаються через хвильові числа. Із цієї причини простір оберненої решітки називають k-простором або p-
простором, оскільки квазіімпульс p = hk .
Деякою мірою аналогом елементарних решіток Браве в оберненому просторі є т.зв. зони Бріллюена. Зони Бріллюена будуються за таким принципом.
Будь-який вузол оберненої решітки (взятий за початковий) з’єднують відрізками з іншими вузлами, а потім через середини цих відрізків проводять перпендикулярні площини. Многогранники, обмежені цими площинами, утворюють зони Бріллюена.
На рисунку 2.4 наведено приклади побудови зон для двовимірної решітки (дві зони) і для прямої ГЦК решітки (перша зона).
Оскільки частота фононів і їх фазова швидкість пов’язані між собою рівнянням ω=kvф, то перепишемо його в такому вигляді:
k2 = k2x + k2y + kz2 = |
ω2 |
|
|
v2 |
(2.7) |
|
ф |
Рисунок 2.4 – Приклади зон Бріллюена для дво- (а) та тривимірної (б) решіток
і одержимо рівняння ізочастотної поверхні, тобто поверхні в оберненому просторі, якій відповідає частота ω=const. Із рівняння (2.7) випливає, що ізочастотна поверхня має сферичну форму, але детальніший аналіз показує, що це має місце лише при малих k і в міру його зростання форма ізочастотної поверхні все більше і більше відхиляється від сферичної.
2.4ТЕПЛОЄМНІСТЬКРИСТАЛІВПРИНИЗЬКИХ
ІВИСОКИХТЕМПЕРАТУРАХ
Згідно із експериментальним законом Дюлонга і Пті молярна теплоємність кристалів при сталому об’ємі (CV) та температурах, близьких до кімнатних, дорівнює 3R (R=8,31 Дж/моль К – універсальна газова стала).
Цей результат повністю відповідає класичній теорії. Дійсно, якщо скористатися теоремою Больцмана про рівномірний розподіл енергії за ступенями вільності, то внутрішню енергію (U) одного моля кристала можна подати так:
U = 3NAε+ U0 |
, |
(2.8) |
% |
|
|
де ε% = kT – середня енергія фонона, яка припадає на один ступінь вільності; U0 – стала складова внутрішньої енергії; k – стала Больцмана (читач повинен розрізняти хвильове число і дану константу).
Із співвідношення (2.8) одержуємо закон Дюлонга і Пті
CV |
|
∂U |
= 3R |
= |
|
||
|
|
∂T V |
. |
Подальші експериментальні дослідження температурної залежності свідчать про те, що закон Дюлонга і Пті виконується лише при високих температурах (рис.2.5), більших за температуру Дебая, яка визначається згідно із співвідношення (2.6).
У зв’язку із цим А.Ейнштейн запропонував квантову теорію теплоємності кристалів, в основу якої покладені такі положення:

-один моль кристала являє собою набір 3NA фононів, частота яких
ω=ω0;
-середня енергія фонона визначається згідно із квантовим співвідношенням Планка
ε% = hhωω0 ekT −1.
Молярну теплоємність можна отримати після диференціювання співвідношення (2.8) за температурою:
|
|
|
|
|
|
|
hω |
|
k |
|
|
hω |
|
|
θE |
2 |
|
θE |
||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
e |
T |
|||||||||||
|
|
∂U |
|
3N |
A |
|
0 |
|
|
|
e |
kT |
|
|
|
T |
|
|
|
|
|
|||
|
|
T2 |
|
|
|
|
|
|
|
|||||||||||||||
CV |
|
|
|
|
k |
|
|
|
|
|
= 3R |
|
|
|
|
|
|
|
||||||
= |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
hω0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
||||||
|
|
∂T V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
e kT |
−1 |
|
|
|
|
|
e T |
−1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, (2.9) |
||
θ |
E |
= |
hω0 |
|
|
k – температура Ейнштейна. |
|||||
де |
|
||||
Рисунок 2.5 – Якісна залежність питомої молярної теплоємності від температури
Оскільки формула Ейнштейна (2.9) складна, то ми пропонуємо її у двох граничних випадках:
θE <<1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) T |
(високі температури) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
CV |
≈ 3R |
|
θ |
2 |
|
|
θ |
E + |
|
+ |
θ |
|
|
+ |
... − |
|
−2 |
|||||
|
|
E |
1+ |
|
|
... 1 |
|
|
E |
1 |
3R |
|||||||||||
|
|
|
T |
|
|
|
T |
|
|
|
|
T |
|
|
|
|
|
, |
||||
θE |
≈1+ θE +... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
e T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
оскільки |
|
|
T |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θE >>1 |
(низькі температури) |
|
|
|
|
|
|
|
|
|
|
|||||||||||
б) T |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
θ |
2 |
− θE |
|
1 |
|
− |
θE |
|
|
||||||
|
|
|
CV ≈ 3R |
|
|
|
E |
e |
T ~ |
|
|
|
|
e |
|
T |
|
|
||||
|
|
|
|
|
|
T |
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
, |
|
|
|||||
θE |
>>1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оскільки e T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким чином, теорія Ейнштейна відповідає експериментальним результатам лише при високих температурах, але із теорії не випливає залежність Cv T (до 1К) або Cv T3 (від 1 до 10К). У той час на відміну від класичної теорії у цьому випадку одержуємо Cv, яка є функцією температури. Причина невідповідності теорії та експерименту пов’язана із неправильним положенням про те, що всі фонони мають постійну частоту ω=ω0. Цей недолік врахований у теорії П.Дебая (1912р.), який припустив, що частота фононів змінюється в інтервалі від 0 до ωmax.
Враховуючи залежність (2.5), можна записати співвідношення для внутрішньої енергії, яка належить до частотного інтервалу dω:
% |
3Vh |
|
ω3dω |
|
||
2 %3 |
|
hω |
||||
dU = εdz = |
|
|||||
|
2π v |
|
|
|
|
|
|
|
ekT −1 . |
||||
|
|
|
||||
Повна молярна внутрішня енергія визначається шляхом інтегрування
|
|
|
|
|
|
3Vh |
ωmax |
|
|
3 |
|
|
|
|
|
3N |
|
h |
ωmax |
3 |
|
|
|
|
|
|
|
|||||||
|
U |
= |
|
|
|
∫ |
|
ω dω |
= |
|
|
|
|
∫ |
ω dω |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 %3 |
|
|
|
hω |
|
3 |
|
|
|
hω |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωmax |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2π v |
|
0 |
|
ekT |
−1 |
|
|
|
0 |
ekT −1 . |
(2.10) |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
hω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Якщо ввести змінну величину |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
kT , то (2.10) перепишеться так: |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
9RT |
4 |
xmax =θD /T |
3 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
U = |
|
|
|
∫ |
|
|
|
|
x dx |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
θ3 |
|
|
|
|
|
|
|
|
ex |
−1 |
, |
|
|
|
|
|
|
||||||
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θD / T x3dx |
|
π4 |
|
θ |
|
|
|
|
|
|
|
|
|
|
|
θ |
|
|
|
|
|
θ |
|
|
|
|||||||||
∫ |
|
|
|
|
|
= |
|
|
|
D → ∞ |
|
;1,18 |
|
|
D = 2 ; 0,225 |
|
|
D =1 |
|
|||||||||||||||
e |
x |
−1 |
15 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
T |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
T |
|
. |
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Співвідношення Дебая у самому загальному випадку запишеться так:
|
|
|
∂U |
|
3R |
|
|
∂ |
|
4 θD / T x3dx |
|
|
||||||||||||
C |
V |
= |
|
|
|
= |
|
|
|
|
|
T |
|
∫ |
|
|
|
|
|
|
|
|
= |
|
|
3 |
|
|
|
|
|
|
|
x |
|
|
|
||||||||||||
|
|
∂T |
|
|
∂T |
|
|
e |
−1 |
|
|
|||||||||||||
|
|
|
|
V |
|
θD |
|
|
0 |
|
|
|
|
|||||||||||
|
|
|
|
|
T |
3 θD / T x3dx |
|
3 |
|
θ |
D |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= 3R |
12 |
|
|
∫ |
|
|
|
|
|
|
− |
|
T |
|
. |
|
|
|||||||
|
|
|
e |
x |
−1 |
θD |
|
|
|
|
||||||||||||||
|
|
|
|
|
θD |
0 |
|
|
|
|
e T |
|
−1 |
|
(2.11) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Як і у випадку теорії Ейнштейна, проаналізуємо рівняння (2.11) у двох граничних випадках:
θD <<1
а) T (високі температури)

|
U = |
9RT4 θD / T x3dx |
|
= |
3RT CV = 3R |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
θ3 |
|
|
∫ ex |
−1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
, |
|||||||||
|
|
|
|
D |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
тобто відповідає експериментальним результатам; |
|||||||||||||||||||
θD >>1 |
(низькі температури) |
|
|
|
|
|
|
|
|
|
|||||||||
б) T |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
9RT4 |
∞ x3dx |
|
|
9R |
π4 |
4 |
|
|||||||||
|
U = |
|
|
|
|
∫0 |
|
|
= |
|
|
15 T |
, |
||||||
|
|
|
θ3D |
|
ex −1 |
|
θ3D |
||||||||||||
|
|
|
|
|
12π4 R |
|
|
|
3 |
|
|
|
3 |
|
|
|
|||
|
|
CV = |
|
|
|
|
T |
|
|
= αT |
, |
|
|
||||||
|
|
|
5θ3D |
|
|
|
(2.12) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
тобто відповідає експериментальним результатам при низьких температурах (т.зв. закон кубів Дебая).
Відсутність залежності Cv T при наднизьких температурах пояснюється тим, що ця залежність не пов’язана із фононною теплоємністю, а відповідає електронній Cvел, яка залишається пропорційною Т у всьому температурному інтервалі.
РОЗДІЛ3 ЕЛЕКТРОННИЙГАЗУМЕТАЛІ
3.1 ІЗОЕНЕРГЕТИЧНІПОВЕРХНІТАПОВЕРХНЯФЕРМІ
Особливістю руху електронів у кристалі є те, що вони мають всі властивості квазічастинок. Із цієї причини, якщо для електрона у вакуумі закон дисперсії енергії ε=p2/2m0 (m0 – маса електрона у вакуумі), то в кристалі він має дещо інший вигляд:
ε = h2k2
2m* ,
де m*=m*(k) – ефективна маса електрона.
Ізоенергетична поверхня в оберненому k – просторі описується рівнянням
k2 = k2 |
+ k2 |
+ k2 |
= |
2m*ε |
|
|
|
h2 , |
(3.1) |
||||||
x |
y |
z |
|
||||
що аналогічне рівнянню (2.7).
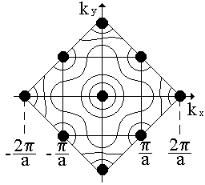
При малих квазіімпульсах ( p = hk ) ізоенергетична поверхня має сферичну форму, але у міру наближення до межі зони Бріллюена має місце все більше і більше відхилення від сфери. На рисунку 3.1 це показано на прикладі перших двох зон Бріллюена.
Оскільки електрони кристалів займають енергетичні рівні відповідно до статистики Фермі-Дірака, то електрони і при Т=0 К будуть мати енергію від 0 до εmax, яка одержала назву енергії Фермі (εф). Ізоенергетична поверхня, яка відповідає εф, має назву поверхні Фермі.
Рисунок 3.1 – Схематичне зображення ізоенергетичних поверхонь електронів у І і ІІ
(випадок, коли валентна зона і зона провідності дотикаються) зонах Бріллюена
3.2 ЕФЕКТИВНАМАСАЕЛЕКТРОНАВКРИСТАЛІ
Закон Ньютона для електрона в кристалі, як квазічастинки, має вигляд

F = h2 a
∂2ε ∂k2 ,
m* = h2 |
|
∂2ε −1 |
|||
|
|
|
|
|
|
∂k |
2 |
– ефективна маса. |
|||
де а – прискорення; |
|
|
|
||
На рисунку 3.2 подана якісна залежність ефективної маси від квазіімпульсу.
Рисунок 3.2 – Послідовні стадії побудови залежності m*=m*(k)
Фізичний зміст m*>m0 полягає у тому, що робота зовнішніх сил F, які прискорюють електрон, частково переходить у кінетичну енергію електрона, а частково у потенціальну енергію решітки. Якщо m*→∞, то це із фізичної точки зору означає, що робота сил повністю переходить у потенціальну енергію решітки (електрон зупиняється). Коли m*<0, то в потенціальну енергію решітки переходить не тільки робота зовнішніх сил, але і частина кінетичної енергії електрона.
3.3КІНЕТИЧНЕРІВНЯННЯБОЛЬЦМАНАДЛЯЕЛЕКТРОНА
ВКРИСТАЛІ. ЕЛЕКТРОПРОВІДНІСТЬМЕТАЛІВ
Кінетичне рівняння Больцмана можна одержати, якщо застосувати теорему rЛіувілляr до функції розподілу електронів за енергіями
f (ε) = f (p, r, t) :
|
r r |
|
|
r |
|
r |
|
|
df (p, r, t) |
= ∂f |
+ ∂fr |
∂p + |
∂fr |
∂r |
= 0 |
|
dt |
∂t |
|||||
|
∂t |
∂p |
∂t |
∂r |
, |
||
∂fr ≡ gradprf ≡ prf |
|
|
|
|
|
|
|
де ∂p |
– градієнт функції розподілу в напрямку |
||||||
∂fr ≡ gradrr f ≡ rr f |
|
|
|
|
|
r |
|
∂r |
– градієнт функції розподілу в напрямку r . |
||||||
r p ;
У реальному кристалі відбуваються процеси зіткнення електронів із фононами, дефектами, домішками та електронами і тому в правій частині замість нуля необхідно записати зміну функції розподілу в результаті вка-
∂f
заних зіткнень – ∂t зт , яку Больцман назвав інтегралом зіткнень. Тоді кінетичне рівняння у самому загальному випадку запишеться так:
∂f |
+ |
∂f |
r |
∂f |
r% |
|
∂f |
|
∂t |
r |
F + |
r v = |
|
(3.2) |
|||
|
∂p |
|
∂r |
|
|
∂t зт , |
||
r
де F – сила, яка діє на електрон; r
v% – середня швидкість дрейфу електрона у зовнішньому електричному полі. r r
Якщо скористатися законом Ома в диференціальній формі ( j = σE , де σ – питома провідність), то можна висунути теорію електропровідності металів.
В імпульсному підпросторі закон Ома перепишеться так:
r |
2e |
r% |
* |
|
j = |
(2πh)3 |
|
dp |
|
∫vf |
||||
|
|
p |
|
, |
де f* – доля функції розподілу Фермі-Дірака, яка пов’язана лише із тими електронами, які беруть участь в електропровідності (їх енергетичні стани розміщуються у розмитті функції Фермі-Дірака, яка показана на рису-
нку 3.3).
Якщо скористатися рівнянням Больцмана (3.2), то можна знайти функцію f* і записати у самому загальному вигляді закон Ома для ізотропних металів:
r |
2e2 |
|
∫ |
r%2 r |
|
|
∂f |
|
|
j = |
|
3 |
|
− |
dp |
|
|
||
(2πh) |
v Eτ |
|
|
||||||
|
|
|
|
|
∂ε |
, |
(3.3) |
||
|
|
|
p |
|
|
|
|
||
∂f
де ∂ε – похідна функції розподілу до прикладення зовнішнього електричного поля (рис.3.3); τ – час релаксації (час, який необхідний для переходу розподілу 3 на рисунку 3.3 у розподіл 2).
