Дисперсияның элементар электрондық дисперсиясы

Жарықтық дисперсиясының классикалық теориясы өзінің бастауы электромагниттік толқындардың (жарықтық) заттың атомдарымен молекулаларының құрамына кіретін зарядталған бөлшектермен өзара әсерлесу жөніндегі мағлұматтардан алады.

Максвелл теориясына сай ортаның абсолют сыну көрсеткіші 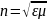өрнегімен анықталады. Диа немесе парамегнетатер босын табылатын мөлдір орталар үшін магниттік өтімділік болады, сондықтан мұндай орталардың сыну көрсеткіші:

Бұдан көрінетіні n- нің толқын ұзындығынан немесе жиіліктен тәуелділігі ортаның диэлектрінің өтімділігі ε сыртқы электр өрісінің жиілігінен тәуелділігінің салдары болып табылады. Жарық толқындарының жиілігі шамамен 10¹⁵ Гц тең, яғни ол осьы үлкен. Олай болса, мұндай жиіліктер кезінде ортаның диэлектрінің өнімділігіне негізгі жарық толқынының электромагниттік өрісінің әсерінен атомдар мен молекулалардағы мәжбүр тербелістерді арқылы анықталатын заттың электрондық поляризациясы қосады. Осылайша, жарықтың дисперсия құбылысын түсіндіру үшін ε диэлектрінің өнімділігінің жиіліктен тәуелділігін теориялық негіздеу қажет. Сонда мына өрнектерді

ескеріп, тұрақты біртекті электр өрісіндегі диэлектрердің поляризациясын қарастырған кезде алынған диэлектриктігін өтімділік ε және n² үшін өрнектерді жазамыз.

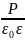; =1+ , (2)

Мұнда -электр тұрақтысы; P және Е заттың 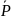поляризация векторының және электр өрісінің 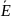кернеулік векторының күш сызықтарын параллель орналасқан Z осіне проекциялары.

Электрондық поляризация үшін поляризацияланғыштық P=n_ap_a (n_a – бірлік көлемдегі атомдар мен молекулалардың саны, яғни олардың ионденпроекциясы; p_a берілген t уақыт моментіндегі атомның немесе молекуланың енгізілген динольдік моментінің Z осіне проекция).

Заттың поляризациялануына, сыртқы, яғни көбірек қозғалғыш валенттік электрондар деп атайды. Бір электронды атомдар үшін (2-сурет) динольдік моменттік проекциясы p_a=-ez, онда поляризацияланғыштық P= n_ap_a=-en_az тең болады. (3). Мұнда е – электрон заряды; z=z(t) жырық толқынының Е(t) электр өрісінің әсерінен белгілі уақыт моментінде тепе – теңдік қалыптан ығысуы.

Олай болса, 2 және 3 өрнектерден

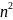=1- 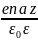(3) тең болады.

Оптикалық электронның тепе – теңдік қалыптан Z ығысу, яғни мәжбүр тербелістердің теңдеуін Ньютонның екінші заңының көмегімен алуға болады.

3-сурет.

Бір жағынан (3-сурет) электронға E=E₀cos(wt-kr+d₀) жарық толқынының электр өрісінің қоздырушы күші әсер етеді:

F_e=-eE=-eE₀cos(wt+d)

Мұнда Z ығысудың аз екендігі ескерілген, сондықтан атомның немесе молекуланың орналасқан нүктесіндегі толқынның бастапқы фазасы 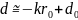тең болады. Екінші жағынан, электронға Z ығысу пропорционал электронның атомның немесе молекуланың басқа бөлімдерімен өзара әсерлесудің квизисерпімді күш әсер етеді: F_cер =kz. Мұнда К коэффициенті оптикалық электронның меншікті тербелісінің w₀ жиілігімен байланысты (k=m_ew^z₀).

Кедергі жоқ кезде электронның мәжбүр тербелісінің дифференциалдық теңдеудің түрі мынадай болады.

(ma_z=F^z_e+F^z_сер):

(4)

Осы теңдеудің дербес шешімін, мысалы, векторлық диаграмманың көмегімен табуға болады:

Сөйтіп z үшін өрнекті 52-формулаға қойып, мына теңдеуді шығарып аламыз:

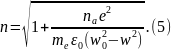
Резонанстық жиілікпен w=w₀ қашықта көптеген мөлдір заттар үшін 54-қатынастағы түбір астындағы екінші қосынды бірден көбірек кіші. Сондықтан ыдырауын пайдаланамыз және ортаның сыну көрсеткіші үшін жуық өрнекті жазамыз:

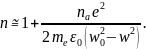
Алынған теориялық тәуелділік счемалық түрде 4-суретте келтірілген.

4 – сурет

Сонда w=w₀ кезінде n=f(w) функциясы +∞-тен +∞-ке дейінсекірмелі түрде өзгереді және ол физикалық мәнге ие емес және пайдаланылған механикалық модельдің салдары болып табылады. Онда кез келген механикалық қозғалыс кезінде кедергі күші бар екендігі ескерілген жоқ. Сондықтан, егер кедергі күшін F_кед.=-μυ 4-теңдеуге енгізсек, онда сыну көрсеткіші үшін өрнекті аламыз. Жарық толқындарының ортамен өзара әсерлескені кезінде энергиясының жұтылатындығы алдын ала ескерілген:

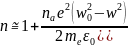
Сөйтіп, 54,a-формуладан w=w₀ тең болған кезде сыну көрсеткіші 1-ге тең (шексіз тәжірибеде бақыланбайтын үзінді байқалмайды) және n-нің w-ден тәуелділігі w жиіліктің үзіліссіз функциясы болып табылады (28,б-сурет). Ал, бұл бұрын келтірілген тәжірибе жүзінде бақыланған n(λ) тәуелділігіменсай келеді (1-суретті қара). Сонда n(w) және n(λ) тәуелділіктерін сәйкестендірген кезде w мен λ арасындағы өзара байланысты ескеру керек 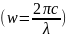. Сондықтан, егер 1-суретте λ₁<λ₂ болса, онда оған сәйкесті жиіліктің мәні 4-суретте w₁>w₂ шартын қанағаттандырады.