
Пособие «Защита информации» (МФТИ)
.pdfпревратить в систему цифровой подписи следующим образом. Пускай Е и D — алгоритмы шифрования и дешифрования соответственно, К и К1 — открытый и тайный ключи. Тогда цифровая подпись ставится по такому правилу: SIGN(M, K1) = DK1(M), а проверку подписи нужно проводить следующим образом: если ЕК(S) = M, то CHECK(K, S) = 1, во всех других случаях CHECK(K, S) = 0.
Итак, рассмотрев общую схему построения цифровой подписи, приступим к описанию конкретных систем цифровой подписи.
Цифровая подпись на основе системы RSA
Напомним, что в криптосистеме RSA каждый абонент сети имеет в своем распоряжении пару ключей: открытый — числа n и e, которые общедоступны, и тайный — число d, который держится в тайне.
Пускай имеем двух абонентов А и В, тогда (ЕA, DA) и (ЕВ, DB) — их алгоритмы шифрования и дешифрования, для которых должно выполняться соотношение: ЕА(DA(M)) = DA(EA(M)) = M и ЕВ(DВ(M)) = DВ(EВ(M)) = M, где М — любое сообщение. Те же соотношения можно записать и в развернутом виде: (M^eA)^dA mod nA = (M^dA)^eA mod nA = M и (M^eВ)^dВ mod nВ = (M^dВ)^eВ mod nВ = M.
Итак, процесс подписывания в данном случае будет происходить следующим образом:
1.Абонент А считает EB(DA(M)) = C и отсылает зашифрованное сообщение С абоненту В.
2.Абонент В считает ЕА(DB(C)) = M.
Корректность данной системы цифровой подписи сводится к соотношению: ЕА(DB(C)) =
ЕА(DB(EB(DA(M)))) = EА(DA(M)) = М.
Конфиденциальность этой системы обеспечивает надежность криптосистемы RSA.
Цифровая подпись в системе Эль Гамала
Аналогично криптосистемам системы цифровой подписи для обеспечения конфиденциальности сообщений допускают вероятностную модификацию. В вероятностных системах цифровой подписи алгоритм SIGN будет не детерминированным, а вероятностным. Таким образом, подпись S будет случайной величиной.
Рассмотрим цифровую подпись в системе Эль Гамала, которая базируется на той же идее, что и соответствующая криптосистема.
Процесс генерирования ключей начинается с выбора большого простого числа р, а также числа g (1 < g < p – 1), причем желательно чтобы число g имело достаточно большой порядок. Числа р и g, не будучи тайными, пребывают во всеобщем использовании абонентов сети. Каждый абонент выбирает случайное число а (1 < a < p – 1) и вычисляет h = g^a mod p. Открытым ключом в данном случае будут числа p, g и h, а тайным — число а.
Для того чтобы поставить свою подпись S на открытом сообщении М, абонент А должен выполнить следующие шаги:
1. Выбирается случайное число r (0 < r < q – 1).
30
2.Вычисляется S1 = g^r mod p.
3.Вычисляется r1 = r^(-1) mod (p –1).
4.Вычисляется S2 = (M – a*S1)*r1 mod (p – 1).
5.В качестве подписи S ставится пара чисел: S = (S1, S2).
Чтобы проверить правильность подписи, абонент В должен проверить выполнение следующего соотношения: g^M = (h^S1)*(S1^S2) mod p.
Система Шнорра
Прежде чем приступить к описанию этой системы цифровой подписи, рассмотрим несколько теоретических понятий. Итак, пускай некоторая функция f отображает сообщение М произвольной длины в виде слова с фиксированной длиной, например, в 128 бит. Если f вычисляется эффективно, то такая функция называется укорачивающей. Причем в системах цифровой подписи используются только такие функции f, при которых для любых сообщений М1 и М2 не выполняется равенство f(М1) = f(М2). Еще одной важной особенностью таких функций является то, что, имея образ М0 (М0 = f(M)), практически невозможно найти сообщение М.
Так вот, для чего все это рассказывается. В системах цифровой подписи целесообразно использовать не само сообщение М, а его укороченный вид f(M). Выигрыш здесь, по-моему, очевиден: алгоритм подписи SIGN постоянно реализуется на входах одинаковой длины, хотя длина сообщения может быть произвольной, т.е. сколь угодно большой. При этом следует отметить, что достоверность подписи не уменьшается.
Вариант укорачивающей функции с ключом называется кодом достоверности. Если f — укорачивающая функция с ключом K, то код достоверности сообщения М равен f(M, K). Тот факт, что значение функции f получено именно для сообщения М и ключа К, может проверить лишь человек, который знает тайный ключ.
Коды достоверности являются криптографическим аналогом контрольной суммы. То и другое присоединяют к сообщениям при пересылке, но контрольную сумму затем, чтобы проверить, не было ли повреждено сообщение, а код достоверности с целью проверки, не была ли часть сообщения заменена каким-то другим.
Следует отметить, что каждую укорачивающую функцию можно преобразовать в функцию с ключом по такому правилу: f1(M, K) = f(M*K).
Примером укорачивающей функции может служить функция, которая строится на основе RSAфункций. На практике же используются более быстрые укорачивающие функции, например, функции MD5 и SHA.
Разобравшись с вышеприведенным теоретическим материалом, приступим к рассмотрению системы Шнорра, названной в честь ее разработчика Клауса Шнорра.
Начнем с процесса генерирования ключей. Выбираем такое большое простое число р, что р – 1 имеет достаточно большой простой делитель q (разработчиком системы рекомендуется выбирать р > 2^512, q > 2^140). Потом выбирают число h, которое удовлетворяет соотношению: h^q = 1 mod p. Числа p, q, h не являются тайными. Далее абонент А выбирает случайное число
31
a, такое что: 1< a <q – 1. Теперь следует найти число V = (h^a)^(-1) mod p. Открытым ключом будет число V, для которого выполняется условие: (h^a)*V = 1 mod p. Тайным ключом выбирается число а.
Перейдем к процессу подписывания, который происходит с использованием некоторой укорачивающей функции f. Для того чтобы поставить свою подпись S на сообщении М, абонент А должен проделать следующие шаги:
1.Выбирается случайное число r (0 < r < q – 1).
2.Вычисляется х = h^r mod p.
3.Находится значение укорачивающей функции S1 = f(M*x), где М*х — слияние сообщения М и числа х в один текст.
4.Вычисляется S2 = (r + a*S1) mod q.
5.В качестве подписи S принимается пара: S = (S1, S2).
Для проверки подписи абонент В находит значение Z = (h^S1)*(V^S2) mod p и проверяет равность S1 = f(MZ).
Система DSA
Напоследок рассмотрим систему цифровой подписи DSA (Digital Signature Algorithm), вышедшую в свет еще в 1991 году и довольно-таки часто называемую DSS (Digital Signature Standart). Именно она применяется в качестве стандарта цифровой подписи.
Традиционно начнем с процесса генерирования ключей. Выбираем достаточно большое простое число р, такое что р – 1 имеет большой делитель q. Стандарт требует, чтобы числа р и q удовлетворяли условиям: 2^512 < p < 2^1024 и q > 2^160. Далее выбирается любое число h, порядок которого совпадает с порядком числа q. Как и в системе Шнорра, числа p, q, h не являются тайной и пребывают во всеобщем пользовании абонентов сети. Чтобы получить открытый и тайный ключи, абонент А выбирает случайное число а и вычисляет b = (h^a) mod p. Тайным ключом является число а, а открытым — число b.
Алгоритм подписи использует укорачивающую функцию f, в качестве которой стандарт рекомендует функцию SHA, являющуюся укорачивающей функцией длиной 160 бит.
Чтобы поставить свою подпись на сообщении М, абонент А должен проделать следующую процедуру:
1.Выбирается случайное число r (0 < r < q – 1).
2.Вычисляется r1 = r^(-1) mod q.
3.Вычисляется S1 = (h^r mod p) mod q.
4.Вычисляется S2 = (r1*(f(M) + a*S1)) mod q.
5.Подпись формируется как пара чисел: S = (S1, S2).
Для проверки подписи абонент В должен вычислить: S0 = S2^(-1) mod q;
U1 = (f(M)*S0) mod q;
U2 = (S2*S0) mod q;
T = ((h^U1)*(b^U2) mod p) mod q.
Успешным результатом проверки следует считать выполнение равенства Т = S1.
32
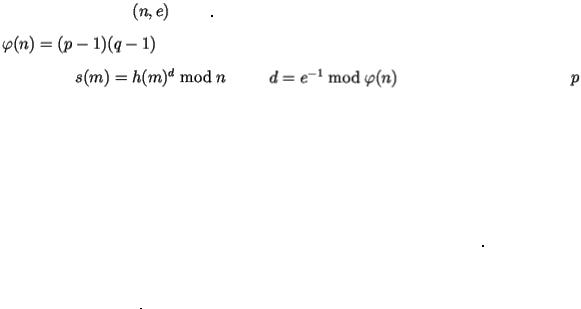
Неофициальный сервер Геологического ф-та МГУ >> М. .. Page 1 of 1
Схемы RSA и Рабина
В данном подразделе мы приводим описание схем подписи, основанных на криптосистемах RSA [RSA] и Рабина [Rab79]. В схеме RSA подписывающий выбирает два различных больших простых числа 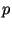 и
и 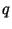 ,
,
которые играют роль секретного ключа, и публикует соответствующий открытый ключ , где , а 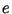 -- некоторое число, взаимно простое с
-- некоторое число, взаимно простое с
(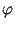 -- функция Эйлера). Подписью для сообщения
-- функция Эйлера). Подписью для сообщения 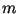
является |
, где |
(очевидно, что, зная и |
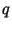 , можно эффективно вычислить
, можно эффективно вычислить 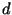 ) и
) и 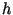 -- хэш-функция. Проверка
-- хэш-функция. Проверка
подписи 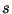 для сообщения
для сообщения 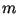 состоит в проверке сравнения
состоит в проверке сравнения
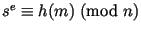 .
.
Схема Рабина основана на том, что, зная различные простые числа 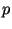 и
и 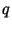 ,
,
можно эффективно извлекать квадратные корни по модулю , тогда как без знания этих простых чисел вышеуказанная задача вычислительно сложна. Секретный ключ в этой схеме тот же, что и в схеме RSA, а открытым ключом является . В качестве пространства сообщений выступает множество всех квадратов элементов группы 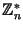 . Подписью для
. Подписью для
сообщения 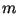 является произвольный квадратный корень из
является произвольный квадратный корень из 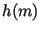 по
по
модулю 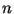 , а проверка подписи
, а проверка подписи 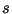 для сообщения
для сообщения 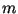 состоит в проверке сравнения
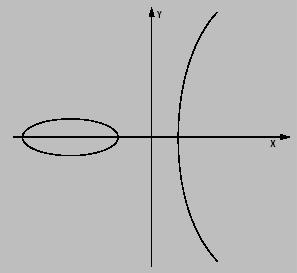
состоит в проверке сравнения 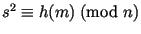 .
.
Схема RSA достаточно эффективна и широко используется на практике. Вера в стойкость обеих схем основывается на (гипотетической) трудности задачи факторизации целых чисел. Для схемы Рабина доказана, в предположении, что эта гипотеза верна, стойкость против пассивного противника (см. следующий подраздел).
33
http://geo.com.ru/db/msg.html?mid=1161287&uri=node38.html 29.05.2004
ЦП на основе эллиптических кривых.
Итак, Е – эллиптическая кривая y=f(x) Если P(x,y) принадлежит кривой, то её точки
удовлетворяют уравнению кривой.
2254<q<2256
d-секретный ключ 1=<d=<q-1 Q=d*P
Открытый ключ: {p,q,P,Q,E} Секретный ключ: d
Создание подписи: А: (M, S(M)) 1.h(M)=e=(e255…e0) (Длина хеш-функции 256 бит)
2.α=(e)mod(q) |
|
|
|
|
|
|
C=kP = (xc;yc) r=xcmod(q) |
|
|
|
3.Выбираем k: |
1=<k=<q-1 |
|
|
|
||||||
4.s=(rd+kα)mod(q) |
|
|
|
|
|
S(M) = (r,s) |
|
|
||
Проверка подписи : B: (M’, S’) S’=(r’,s’) |
|
|
||||||||
1.Во-первых, r’<q , s’<q |
|
|
|
|
|
|
||||
2.h(M’)=e’ |
|
|
|
|
|
|
|
|
|
|
3.α’=e’mod(q) |
|
|
|
|
|
|
|
|
|
|
4.C’=(α’)-1 s’P - (α’)-1 r’Q = (xc’;yc’) (всё по модулю q) |
|
|
||||||||
5.R=xc’ mod(q) и если это равно r’ то подпись принимается. |
|
|
||||||||
Проверка корректности |
|
|
|
|||||||
h(M)=e; α=e mod(q) |
|
|
|
|
|
|
||||
C’=(α)-1sP - (α)-1rQ = (α)-1sP - (α)-1r*d*P = (α)-1(s-rd)P = (α)-1kαP = kP = (xc;yc); а |
xc |
|
||||||||
mod(q)=r. |
|
|
|
|
|
|
|
|
|
|
Как производятся операции над точками эллиптических кривых: |
|
|
||||||||
Если P,Q принадлежат кривой G то P+Q тоже принадлежит G. |
|
|
||||||||
P(x1,y1) + Q(x2,y2) = R(x3,y3) : |
|
|
|
|||||||
2 |
|
|
|
|
y2 − y1 |
|
|
|
||
x3 = λ -x1-x2 |
|
|
|
λ = |
|
|
|
- наклон кривой |
|
|
|
|
x |
2 |
− x |
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
y3 = - y1 + λ(x1-x3) |
|
|
|
|
|
|
3x 2 |
|
||
Если P=Q то λ |
= |
dy |
|
|
например, если у нас кривая y2=x3 + ax + b то λ = |
+ a |
||||
|
|
|||||||||
|
|
|
1 |
|
||||||
dx |
|
x1, y1 |
2y |
|||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
34
Эллиптические кривые. |
Page 1 of 4 |
Эллиптические кривые.
Виктор Миллер, Нэйл Коблиц
Эллиптические кривые обеспечивают другое основание, на котором могут быть построены криптографические алгоритмы.
Здесь, вместо работы строго с остатками по модулю p, мы имеем дело с геометрическими отношениями. Первичным преимуществом эллиптических кривых является то, что в сложных геометрических вычислениях существует более трудный (для раскрытия) аналог проблемы дискретного логарифма (или, по крайней мере, который не столь хорошо понят). Для этой задачи требуются более короткие простые числа p. И, конечно, с более короткими простыми числами, криптографические алгоритмы будут работать значительно быстрее.
Здесь простое p является открытым и используется в уравнениях следующего вида:
y^2 = x^3 + ax + b mod p (обозначается, как нормальная форма Вейерштрасса)
Кроме того, вышеуказанное уравнение подчиняется следующему ограничению:
4a^3 + 27b^2 != 0 mod p
Таким образом, эллиптические кривые состоят из точек:(x,y):
y^2=x^3+ ax + b mod p, которые симметрично расположены относительно x-оси.
Кроме того, мы добавим дополнительную точку, I, которая представляет собой точку на бесконечности. Итак, у нас имеется конечное множество решений этого уравнения, с p + t + 1 парами точек, где |t|<=sqrt(p).
Другими словами, точки на эллиптической кривой формируют конечное абелево множество и могут таким образом использоваться подобным способом для полей и всего такого. Теперь определим основные операции на этом
множестве.
35
http://www.ib.kgtu.runnet.ru/articls/kript_eliptich.htm 29.05.2004
Эллиптические кривые. |
Page 2 of 4 |
Эллиптическая кривая, состоящая более чем из одного "сегмента" (многосвязная).
Можно видеть процесс сложения точек P и Q (также, как R + R), объясняемый ниже. Обратите внимание на специальную точку I и вертикальную линию, соединяющую ее и точки S и -S.
Сложение определяется следующим образом: сумма P + Q, где P и Q - точки где-нибудь на кривой, является {\it отражением} третьей точки кривой, которой касается (или которую пересекает) линия, соединяющая P и Q (по существу, используются касательные и хорды; смотри
рисинок).
Если P и Q - одна и та же точка ( скажем, P = Q = R ), то сумма записывается [2]R (или, более просто, 2R ), где линия, "соединяющая" две точки R - просто касательная к кривой в точке R. Поскольку I - на бесконечности, линия, соединяющая P и I, вертикальна и
просто пересекает эллиптическую кривую, давая отражение P (-P). Таким образом, отражение этой точки (-P) - просто P; и, эффективно, I - выполняет функцию идентичности для этого конечного множества. Эквивалентно, если линия, соединяющая точки P и Q вертикальна ( Q = -P ), то их сумма равна I, поскольку эта линия снова "касается" эллиптической кривой в точке на бесконечности.
Более формально, определим сложение с помощью
36
http://www.ib.kgtu.runnet.ru/articls/kript_eliptich.htm 29.05.2004
Эллиптические кривые. |
Page 3 of 4 |
геометрии, вычисляя уравнение для линии между P и Q как
$y=lambda*x + beta,
находя третью точку пересечения между эллиптической кривой и этой линией, и последовательно взяв отражение этой точки в качестве суммы. Следующий алгоритм
обрисовывает эту процедуру:
Дано: P =x_1,y_1, Q = x_2,y_2,
если (x_1= x_2)&(y_1 = -y_2), то (P+I):= I(Q=-P).
если (x_1= x_2), то lambda = (3x_1^2 + a)/(2y_1) mod p,
(где lambda - наклон, т.е. эта формула получена взятием производной в точке (x_1,y_1)).
иначе lambda = (y_2 - y_1)/(x_2-x_1) mod p
Определим beta = y_1 - lambda*x_1.
Тогда, x_3 =lambda^2- x_1x_2,
y_3 =-(lambda*x_3 +beta) P+Q := (x_3,y_3) mod p.
Эта операция сложения - коммутативна, также как ассоциативна (что несколько удивительно; доказательство - вне возможностей этого курса ). Таким образом, мы получаем систему, где мы можем определить сложение
аналогично умножению по модулю p.
Мы используем следующую нотацию для этого множества чисел.
E_n(a,b) = множество точек эллиптической кривой,которые удовлетворяют:
-y^2 = x^3 + ax + b
-gcd(4a^3+27b^2,n) =1
плюс содержит специальную точку I.
37
http://www.ib.kgtu.runnet.ru/articls/kript_eliptich.htm 29.05.2004
Эллиптические кривые. |
Page 4 of 4 |
E_p, для простого p, представляет эллиптическую группу
N_p(a,b) = порядок E_p(a,b).
O(E_p)(M) = порядок элемента M в E_p.
Итак, теперь, вместо умножения, мы используем операцию сложения, определенную выше. Последовательным образом, вместо вычисления степени по модулю g^k mod p, мы "умножаем" P (эквивалент g в этом эллиптическом царстве) на k(=[k]P),определяя, как: P + P + P + P. .. + P (k раз). Это делает "дискретную проблему логарифма" эквивалентной обнаружению того, сколько раз точка P должна быть добавлена к себе, чтобы равняться другой
точке Q.
38
http://www.ib.kgtu.runnet.ru/articls/kript_eliptich.htm 29.05.2004
Цифровая подпись. Эллиптические кривые |
Page 1 of 2 |
Эллиптические кривые и новый стандарт на электронную подпись
До сих пор мы говорили в основном о числах. Но математики уже давно не работают только с числами. Алгебра имеет дело с «объектами», их «свойствами» и операциями, определенными на множестве данных объектов. Примерами могут служить множество комплексных чисел, поле многочленов с рациональными коэффициентами и т.д. Так вот, группа точек эллиптической кривой, являясь первоначально абстрактным алгебраическим объектом, оказалась удобной для построения алгоритмов цифровой подписи.
«Эллиптической кривой» называют множество пар точек (X,Y), удовлетворяющих уравнению:
y2 = ax3 + bx + c
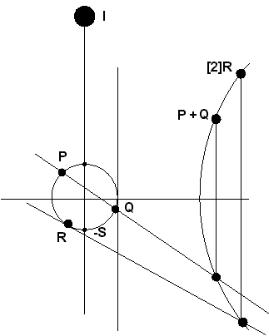
Можно наложить ограничения на множество значений переменных х, y, и коэффициентов a, b, c. Ограничивая область определения уравнения значимым для приложений числовым множеством (полем) мы получим эллиптическую кривую, заданную над рассматриваемым полем. На рис. 2 изображен общий вид эллиптической кривой, определенной на множестве действительных чисел.
Рис. 2. Общий вид эллиптической кривой
В приложении к криптографии (и в новом стандарте на цифровую подпись) эллиптическая кривая над конечным простым полем GF(p) определяется как множество пар (x,y), таких что x,y ≡ GF(p), удовлетворяющих уравнению:
y2 = x3 +ax +b (mod p), a, b ≡ GF(p)
Пары (x,y) будем называть «точкой». Точки эллиптической кривой можно «складывать». «Сумма» двух точек, в свою очередь, тоже «лежит» на эллиптической кривой.
Кроме точек, лежащих на эллиптической кривой, рассматривается также «нулевая точка». Считается, что сумма двух точек A с координатами (XA, YA) и B с координатами (XB,YB)
равна O, если XA = XB, YA = –YB (mod p). Нулевая точка не лежит на эллиптической
кривой, но, тем не менее, участвует в вычислениях; ее можно рассматривать как бесконечно удаленную от кривой.
39
http://www.osp.ru/os/2002/07-08/010_1_print.htm |
29.05.2004 |
