
Основы наноелектроники / Основы наноэлектроники / ИДЗ / Книги и монографии / Эффект фотонной лавины в кристаллах и наноструктурах. Монография (Перлин), 2007, c.120
.pdf
лавины, описанной в § 1.1, то n-фотонные переходы v → c играют роль слабых нерезонансных переходов 1 → 2, l-фотонные переходы c → с1 соответствуют быстрым резонансным переходам 2 → 3, а переходы c1 + (n –
l)hω → ccv играют ту же роль, что кросс-релаксация.
Мы будем называть предлагаемый здесь механизм генерации элек- трон-дырочных пар многофотонной лавиной.
Рассматриваемая модель, естественно, включает также релаксационный процесс c1 → c с участием фононов и процессы рекомбинации нерав-
новесных фотовозбуждённых электронов и дырок.
Очевидно, что предложенная модель может работать лишь в области очень сильных электромагнитных полей (Fω t 107 В/см). При hω = 1.17 эВ,
mr = 0.4 m ( m−1 |
= m−1 |
+ m−1 , m – масса свободного электрона), Eg = 5.7 эВ, |
|
r |
c |
v |
|
Fω = 107 В/см параметр Келдыша [84, 85] |
|
||
|
|
γ =ω mr Eg eFω |
(5.3) |
принимает значение γ ≈ 6.4. Большая величина параметра γ позволяет заключить, что в области интенсивностей меньших 1013 Вт/см2 в рассматриваемой ситуации адекватной является картина многофотонных межзонных переходов, а не межзонного туннелирования в поле сильной электромаг-
нитной волны. При этом неравенство 1 (4γ )2 <<1 позволяет утверждать,
(4γ )2 <<1 позволяет утверждать,
что между заданными зонами фактически будут идти переходы с наименьшим числом фотонов, допускаемым законами сохранения3 . Для оценки вероятностей многофотонных межзонных переходов далее будут использоваться результаты работ [86], [87], где получены формулы для ве-
роятностей n-фотонных межзонных переходов Wvc(n) ≡σvc(n) jn при произ-
вольных n. В области малых j для n = 3 эти формулы совпадают с полученными в рамках стандартной теории возмущений. При n >> 1 формулы из [86, 87] дают асимптотику, близкую к той, что получена Л.В. Келдышем в [84] и Ю.А. Бычковым и А.М. Дыхне [85].
Как уже отмечалось выше, ключевую роль для запуска процесса многофотонной лавины играют переходы оже-типа c1 + shω → ccv ,
s = n −l . Вычислению вероятностей этих переходов Wa(s) ≡ γ (s) jsnc1 посвящен следующий параграф.
§ 5.3. Расчет вероятностей многофотонных переходов оже-типа
Представим гамильтониан электрон-фотонной системы в виде
3 Такая ситуация является типичной, но бывают исключения. Так в работе [110] показано, что в непрямозонном материале AgBr благодаря особенностям электронной зонной структуры и проявлениям оптического эффекта Штарка в условиях двойного межзонного резонанса вероятности n-фотонных межзонных переходов с n = 3 и n = 4 оказываются в при j t 1010 Вт/см2 (λ = 560 нм) бóльшими, чем вероятности переходов с n = 2.
73

ˆ |
ˆ (0) |
ˆ (0) |
+ |
ˆ |
ˆ |
, |
(5.4) |
H = He |
+ Hphot |
He′-phot + He′′-phot + |
He′-e |
||||
где |
|
|
|
|
|
|
|
ˆ (0) |
|
+ |
|
ˆ (0) |
+ |
|
(5.5) |
He |
= ∑εi (k)ξikξik |
, Hphot = ∑hωκcκλcκλ |
|||||
|
i,k |
|
|
κ,λ |
|
|
|
– гамильтонианы невзаимодействующих подсистем свободных электронов и фотонов,
ˆ |
|
κλ |
|
κλ + + |
|
|
He′-phot = ∑(Vki,k′jcκλ |
+Vk′j,kicκλ ) ξikξjk′, |
(5.6) |
||||
|
′ |
|
|
|
|
|
|
ki,k j |
|
|
|
|
|
|
|
1 2 |
′ |
|
|
|
V κλ ′ |
= −ieh |
2πh |
|
ki eκλ k j |
, |
(5.7) |
L3 |
|
[ωκεT (ωκ,κ)]1 2 |
||||
ki,k j |
m |
|
|
|
||
– линейная по полю часть электрон-фотонного взаимодействия, |
He′′-phot – |
|||||
квадратичная по полю часть электрон-фотонного взаимодействия, отличная от нуля лишь при учете малого волнового вектора фотона κ,
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
He′-e |
= |
∑ k0i,k3 j Ve-e k1i′,k2 j′ |
|
+ |
+ |
|
|
|
(5.8) |
||||||
|
ξk0iξk3 jξk1i′ξk2 j′, |
|
|
||||||||||||
|
k i,k i′, |
|
|
|
|
|
|
|
|
|
|
||||
|
k30 j,k12 j′ |
|
|
|
|
|
|
|
|
|
|
||||
|
ˆ |
|
|
|
|
|
|
4πe2δk0 +k3 ,k1+k2 |
|
ii′ |
jj′ |
, |
(5.9) |
||
k0i,k3 j Ve-e k1i′,k2 j′ |
= |
|
% |
|
|
2 |
3 βk0k1 |
βk3k2 |
|||||||
|
|
|
|
|
|
|
εL (Ω,k0 −k1) k0 −k1 |
L |
|
|
|
||||
|
|
|
|
|
|
|
|
|
1, |
|
′ |
|
|
|
|
|
βk,kii′ |
|
= |
1 |
∫uik (r)ui′k-q (r)dr ≈ |
i = i , |
|
|
(5.10) |
||||||
|
-q |
|
ii′ |
|
′ |
|
|
||||||||
|
|
|
|
|
|||||||||||
|
|
|
V |
|
|
|
|
βq |
|
|
|
|
|||
|
|
|
|
|
|
|
i ≠ i , |
|
|
|
|||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
где величины |
βqii′ |
~ h2q2 |
(2m |
E ) <<1, |
E обозначает характерный зазор |
||||||||||
между зонами. В формулах (5.4-5.10) использованы следующие обозначения: m – масса свободного электрона; V0 – объем элементарной ячейки;
εi(k) – блоховская энергия электрона в i-ой зоне; ξi+k , ξik – операторы рождения и уничтожения для состояний с волновым вектором k в i-й зоне, которые заменяются на электронные операторы ai+k , aik или дырочные операторы bik , bi+k , когда индекс i пробегает значения, соответствующие зонам
проводимости либо валентным зонам; κ, ωκ, λ и eλ – волновой вектор, частота, индекс поляризации и единичный вектор поляризации фотонов;
cκ+λ ,cκλ – операторы рождения и уничтожения фотонов; εL(ω,q) и εT(ω,q) – продольная и поперечная диэлектрические проницаемости, зависящие от частоты и волнового вектора, переданная при межэлектронных столкнове-
ниях частота Ω% дается выражением Ω% = h−1[εi (k0 ) −εi′(k1)].
74
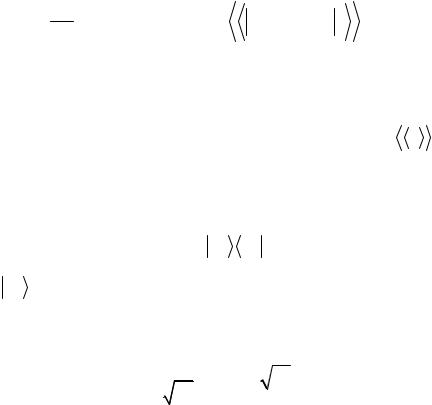
Оценка матричных элементов операторов He′-phot и He′-e с использова-
нием k p - теории возмущений приводит к следующему результату: отношение внутризонного матричного элемента оператора электрон-фотонного взаимодействия He′-phot к межзонному матричному элементу пропорцио-
нально величине βkii′ <<1, а в случае кулоновского взаимодействия He′-e отношение межзонного матричного элемента к внутризонному пропорционально величине βqii′ [см. формулы (5.6-5.10)].
Выражение для вероятности многофотонного перехода из зоны v в зону c с участием свободных носителей из зоны c1 запишем в виде:
Wa(l ) = 2π |
∑ fc1k0 (1− fvk3 ) Md(l ) + Mexc(l) 2 |
× |
|
h |
k0 ,k1 ,k2 ,k3 |
phot |
(5.11) |
|
|
, |
|
×δ εc1 (k0 ) +εv (k3 ) −εc (k1) −εc (k2 ) + lhω |
|
||
где fik – функция распределения электронов в i-й зоне, |
Md(l ) и Mexc(l ) – пря- |
||
мой и обменный вклады в составной матричный элемент, |
phot – обозна- |
||
чает усреднение по состояниям фотонной подсистемы. Для усреднения используется т.н. диагональное представление Глаубера [102, 103] с оператором плотности электромагнитного поля
ρ |
phot |
= |
∫ |
P({ξ |
κ |
})Π ξ |
κ |
ξ |
κ |
d 2ξ |
κ |
, |
(5.12) |
|
|
|
κ |
|
|
|
где ξκ и ξκ собственные значения и собственные функции оператора cκ.
Излучение одномодового идеального стабильно генерирующего лазера описывается δ-образной диагональной весовой функцией
P(|ξκ |) = |
|
1 |
δ (|ξκ | − nκ ), |
(5.13) |
|
2π |
n |
||||
|
|
|
|||
|
|
κ |
|
|
где nκ – среднее число фотонов в моде.
В формуле (5.11) учтено, что из законов сохранения энергии и импульса следует, что конечные состояния электронов в зоне c удалены от дна зоны и могут считаться незаполненными.
Матричные элементы перехода будем вычислять в (l + 1)-м порядке теории возмущения – l порядков по взаимодействию He′-phot и один порядок
по взаимодействию He′-e . Вводя обозначение
(5.14)
запишем критерий применимости борновского приближения по межэлектронному взаимодействию He′-e для рассматриваемой задачи в виде
75
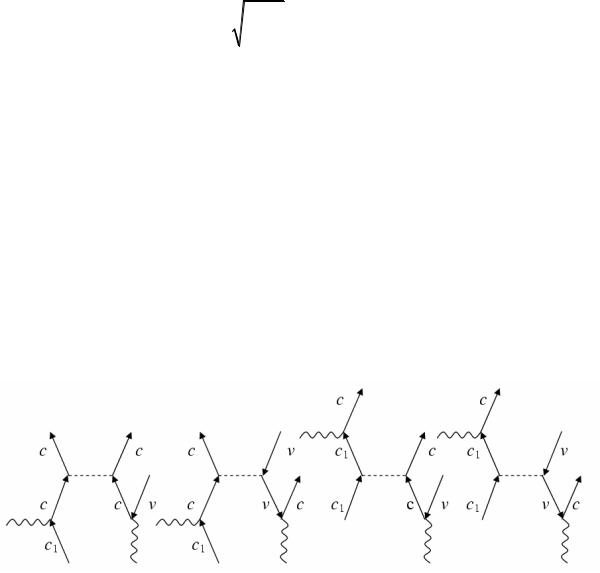
|
|
e2 |
|
|
m |
|
<<1. |
|
|
|
|
|
|
c |
|
(5.15) |
|
|
|
εlh |
2 (l ) |
|||||
|
|
|
|
|
|
|||
Условие (5.15) выполняется для не очень малых значений |
(l). |
|||||||
Критерии применимости теории возмущений по He′-phot имеют вид: |
||||||||
|
eFω pcv |
|
<<1, |
ωR(s)τ p <<1, |
(5.16) |
|||
|
m Eg hω |
|
||||||
|
|
|
|
|
|
|
||
где pcv – межзонный матричный элемент оператора импульса, Fω – амплитуда электрического поля световой волны, ωR(s) – s-фотонная частота Раби (s = 2 или 3) для переходов между зонами c и c1, τp – время релаксации импульса электронов, ωR(s) js 2 , где j – интенсивность излучения. Первое из
2 , где j – интенсивность излучения. Первое из
условий (5.16) выполняется для всех актуальных интенсивностей, тогда как второе при s = 2 выполняются лишь при j d 1012 Вт/см2. При более высоких интенсивностях, вообще говоря, требуется учет эффектов переизлучения фотонов.
Рис. 5.2. Диаграммы, представляющие прямой вклад в процесс в случае модели А: сплошные линии со стрелками вверх (вниз) – электроны (дырки), волнистые – фотоны, пунктирные – кулоновское взаимодействие
Из множества диаграмм Фейнмана выберем те, которые вносят основной вклад в процесс. В случае модели А это диаграммы, в которых присутствуют только межзонные матричные элементы оператора электронфотонного взаимодействия и внутризонный матричный элемент оператора кулоновского взаимодействия. На рис. 5.2 представлены диаграммы, дающие прямой вклад в составной матричный элемент. Для модели В при выборе диаграмм считаем, что переходы из зоны v в зону c1 запрещены. Как показывает анализ, в этом случае удается выделить две диаграммы, вклад
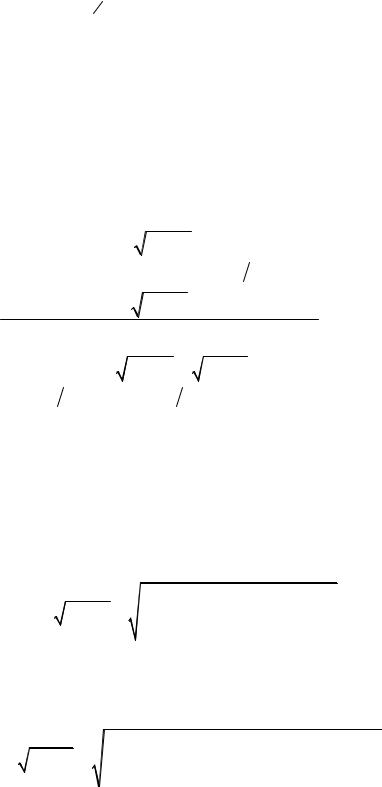
которых в (βqii′)−2 раз больше вклада остальных диаграмм (рис. 5.3).
76
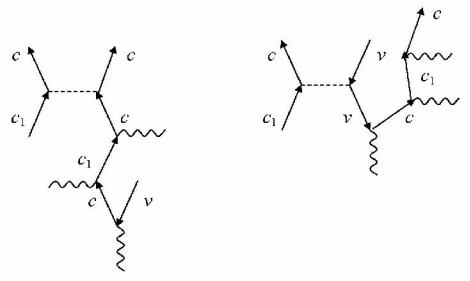
Рис. 5.3. Диаграммы, представляющие прямой вклад в случае модели В (обозначения такие же, как на рис. 5.2)
Для получения формул в виде, удобном для численных расчетов, используем следующие упрощающие предположения: будем считать, что зоны v, c, c1 являются параболическими с экстремумами в центре зоны Бриллюэна в точке k = 0, а электроны в зоне c1 сосредоточены вблизи экстремума зоны, так что можно положить k0 = 0 .
Прямой вклад составного матричного элемента запишем в виде:
|
(2) |
|
(2) δk0 +k3 ,k2 +k1 |
|
|
|
−1 |
|
|
|
−1 |
|
|
|
|
|
−1 |
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|||||||||||||||||
Md |
|
= C0 |
|
|
|
|
|
|
|
|
|
|
Bc |
(k1) − Bc |
(k0 ) Bv0 (k2 ) |
− Bv0 |
(k3 ) |
, |
|
||||||||||||||||||||||||||||
|
|
|
|
k0 −k1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
M |
(3) |
= C |
(3) |
C |
δk |
+k |
,k |
+k |
1 |
B−1(k |
2 |
)B−1 |
(k |
2 |
) |
− |
B−1 |
(k |
3 |
)B−1(k |
3 |
) |
, |
|
|||||||||||||||||||||||
|
|
|
0 |
|
3 |
2 |
|
|
|
|
|
c |
|
v2 |
|
|
|
v0 |
|
|
v2 |
|
|
|
|
|
|||||||||||||||||||||
|
d |
|
|
0 |
|
|
q |
|
|
k0 −k2 |
|
|
|
|
2hω |
|
|
|
|
|
|
Bc (k3 ) + Bv2 (k3 ) |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
h (e |
λ |
q) |
|
|||||
(l ) |
|
|
4πe2 |
|
|
e A l (eλ pcv )(eλ pcc ) |
|
|
|
Сq = 2 |
cc |
|
|
|
|
|
|
, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С0 = |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
, |
|
|
|
|
|
m [εc |
(0) −εc (0)] |
|
|||||||||||
|
3 % |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
L εL (Ω) |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Bc (k) = (ζ ′−1)εc (k) +δc , Bvn (k) = (ζ +1)[εc (k) +δv ] − nhω,
(5.17)
(5.18)
(5.19)
δc =εc (0) −εc (0) + hω, |
δv = |
Eg − hω |
. |
|
|||
1 |
|
1+ζ |
|
|
|
|
|
В приведенных выше выражениях pcv |
и pc c − межзонные матричные |
||
|
|
1 |
|
элементы оператора импульса, A0 – амплитуда вектор-потенциала свето-
вой волны, с – скорость света в вакууме, ζ = mc  mv , ζ ′ = mc
mv , ζ ′ = mc  mc1 , mi – эффективная масса частиц в i-й зоне. Выражение для обменного вклада составного матричного элемента можно получить из формул (5.17), (5.18) путем замены k1 ↔ k2 .
mc1 , mi – эффективная масса частиц в i-й зоне. Выражение для обменного вклада составного матричного элемента можно получить из формул (5.17), (5.18) путем замены k1 ↔ k2 .
77
После довольно громоздких вычислений получим следующее выражение для вероятности переходов:
|
|
|
|
|
|
|
210 e2(l+2) |
|
p |
|
2 |
|
p |
|
2 m |
(l−1) |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
W (l ) |
= |
|
|
|
|
|
|
|
|
cv |
|
|
|
|
cc1 |
|
|
|
c |
|
|
n jl I |
, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
a |
|
|
|
|
|
2 (hω m)2 |
|
clζ (1+ζ )2 |
|
c |
l |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
εL2εT |
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b1 b2 |
|
|
|
|
|
|
′ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
I2 =π h ∫∫dx dy |
(ζ |
−1) f2 |
|
× |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
2 |
( y − x) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a a |
2 |
|
|
|
|
|
δc |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y − (1+ζ )x + (δc |
+δv )ζ |
|
2 |
|
|||||||||||||||||||
(1+ζ ) y − x |
|
|
|
|
|
|
|
|
|
, |
|||||||||||||||||||||||||||
× |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−ζ ′)x +δcζ ′] |
|
[δc − (1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
y[(1 |
|
|
−ζ ′)( y −δv )](δc +δv − x) |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d1 d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f3 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
I3 = |
2π |
2 |
h |
3 |
∫∫dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|||||||||
|
|
|
(δc − hω) |
2 |
(δc |
− x)( y −δv ) |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
c c |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y −δv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
[(ζ ′−1)( y |
−δ |
|
) +δ |
|
|
][y − 2hω (1+ζ )] |
|
|
|
||||||||||||||||||||||||||
|
|
|
v |
c |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ− x
+[(1−ζ ′)x +ζ ′δc ][δc +c δv − x − 2hω (1+ζ )]−
(1+ζ )]−
|
|
|
|
|
|
4ζ |
2 |
hω( y −δv |
+ δc − x) |
|
|
2 |
|
|||||||||||
− |
|
|
|
|
|
|
|
|
|
, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(1 |
+ζ )z[z + 2ζ hω (1+ζ )] (1+ζ |
′ ζ )z + (ζ ′ |
−1)δv −δc + 2hω |
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
v |
|
|
|
|
|
p |
|
B |
} |
|
|
||
|
|
f |
|
= |
1+ exp[( y − x +δ ζ + μ |
|
)/ k T ] −1 , |
|
|
|||||||||||||||
|
|
|
|
|
3 |
{ |
|
|
|
|
v |
|
|
|
|
p |
|
|
B |
} |
−1 , |
|
|
|
|
|
|
|
f |
|
= 1 |
+ exp[(z +δ ζ + μ |
|
)/ k T ] |
|
|
|||||||||||||
|
|
a |
|
= |
(1+ζ )2 δ |
|
+ |
ζ |
|
δ |
|
, b1 =δc , z = y − x − hω , |
|
|
||||||||||
|
|
|
v |
1+ 2ζ |
c |
|
|
|||||||||||||||||
|
|
1 |
|
|
1+ 2ζ |
|
|
|
|
|
|
|
|
|
|
|
||||||||
(5.20)
(5.21)
(5.22)
a2 |
|
|
|
ζ |
|
2 |
|
|
|
|
|
|
|
1+ 2ζ |
|
|
|
δ |
|
|
1+ζ |
|
2 |
2 |
|
|
||||||
|
|
|
|
δc − x m |
|
x |
|
|
|
|
|
|
(5.23) |
|||||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
c − |
|
|
|
|
δv |
+δv |
|||||||||
|
1+ζ |
|
|
|
|
|
ζ |
2 |
|
|
ζ |
|
||||||||||||||||||||
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ζ |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
= |
(1+ζ )2 |
δ |
|
+ |
|
|
ζ |
δ |
|
|
− |
|
1+ζ |
|
hω , |
d =δ |
c |
, |
|
|
|
||||||||
|
|
1+ 2ζ |
|
|
1 |
+ 2ζ |
|
|
1 |
+ 2ζ |
|
|
|
|||||||||||||||||||
|
1 |
|
|
|
v |
|
|
c |
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||
c |
|
|
ζ |
2 |
|
= |
|
|
1+ζ |
||
d2 |
|
||
|
2 |
|
|
|
|
δc − x m |
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ 2ζ |
|
δ |
|
|
1+ |
ζ |
2 |
1+ζ |
2 |
|
||||
x − |
|
|
|
|
||||||||||
|
|
|
c − |
|
|
|
|
δv + |
|
|
hω |
+δv |
||
ζ |
2 |
|
|
ζ |
|
ζ |
2 |
|||||||
|
|
ζ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
78
где nc1 – концентрация частиц в зоне c1, μp – химический потенциал дырок в зоне v, kB – постоянная Больцмана, T – температура кристалла, остальные величины, фигурирующие в формулах (5.20-5.23), были определены выше.
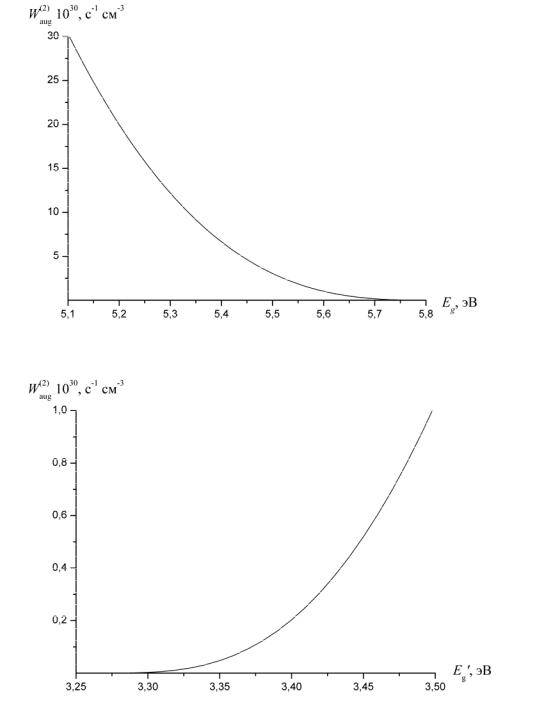
Рис. 5.4. Зависимости вероятности двухфотонного процесса оже-типа от параметров зонной структуры (модель А)
Перейдем к обсуждению результатов численных расчетов. На рис. 5.4 и 5.5 приведены графики рассчитанных по формулам (5.20-5.23)
79

зависимостей W |
(l ) |
от некоторых параметров зонной структуры. При этом |
||||||||||||||
|
|
|
|
|
a |
|
|
|
|
таковы: для модели А |
|
mc = 0.6 m , |
||||
значения |
остальных |
|
параметров |
– |
||||||||||||
mc |
= 0.01 m , |
mv = 0.8 m, Eg = 5.6 |
эВ, |
Eg′ = 3.5 |
эВ, εT = 4.6 , |
εL =12.4 , |
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
=1018 см-3, |
p |
= p |
|
=10−19 г см/с, hω =1.17 эВ, |
j =1011 Вт/см2; для моде- |
||||||||||
|
c |
|
|
|
cc |
|
cv |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
Eg′ = 2.32 |
|
||
ли В – mc = 0.6 m , |
mc |
= 0.1 m , |
mv = 0.8 m , Eg = 5.6 эВ, |
эВ, |
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
ε |
T |
= 4.6 , |
ε |
L |
=12.4 , |
n |
=1018 см-3, |
p |
= p =10−19 г см/с, |
hω =1.17 |
эВ, |
|||||
|
|
|
|
|
|
|
c |
|
cc |
cv |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
j=1011 Вт/см2.
Вработах [86, 87] были получены следующие формулы для вероятности W(5) «обычного» прямого пятифотонного перехода между зонами v и c:
|
|
|
|
|
|
(5) |
|
|
|
|
2E0c mc3/ 2 |
|
ρ 2 |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
Wvc |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| g | , |
|
|
|
|
|
|
(5.24) |
||||||
|
|
|
|
|
|
πh |
4 |
(ζ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1) |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ = |
|
1 |
|
|
10 |
|
V |
|
2 |
− |
|
Vcc |
|
2 |
c c |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
vc |
|
|
1 |
|
|
1 |
|
, |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4hω |
|
|
24hω |
|
|
|
|
c2 c − (hω)2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g = − |
|
V |
|
|
|
5|V |
|
|
|
| |
+ |
|Vcc |
|
|2 (5hω −3 |
c c ) |
, |
|
|
(5.25) |
|||||||||||||||||
|
|
|
|
vc |
|
|
|
|
|
|
vc |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||
|
|
144hω |
|
|
|
|
|
|
|
|
|
2 |
|
− (hω)2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
6hω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c c |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
E |
= |
5hω − Eg |
|
, |
|
c c |
= ε |
c |
|
|
(0) −ε |
(0) , |
V |
= |
|
|
8π j |
|
|
e pij |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
0c |
|
ζ +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
ij |
c |
εT (ω) |
|
mω |
|
|||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Сравнение полученных величин вероятностей Wa(l ) процессов оже-
типа c1 + lhω → cc (l = 2, 3) c рассчитанной по формулам (5.24, 5.25) вероятностью W(5) прямого пятифотонного перехода между зонами v и c при тех же значениях параметров зонной структуры вероятностью показывает,
что при |
p |
= p |
=10−19 г см/с, hω =1.17 эВ, j =1011 Вт/см2 и n >1017 |
1/см3 |
|
cc |
cv |
c |
|
|
1 |
|
1 |
|
W (l ) >>W (5) |
. Это справедливо как для модели А, так и для модели В. Ука- |
|||
a |
vc |
|
|
|
занное обстоятельство является весьма важным для кинетики предпробойной генерации электрон-дырочных пар в широкозонных материалах, так становится возможным запуск процесса типа фотонной лавины. Кинетике специфической многофотонной лавины, где размножения электронов в возбужденных состояниях обеспечивается за счет рассмотренного в данной работе процесса, будут посвящены следующие параграфы.
80
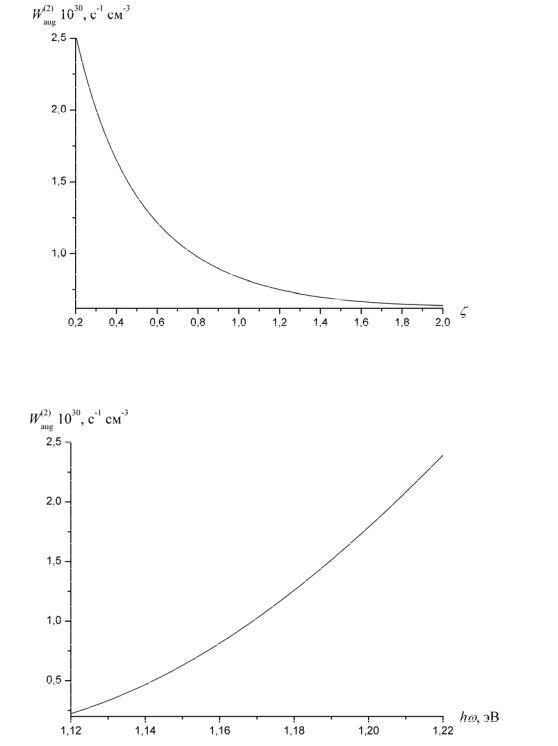
Рис.5.5. Зависимости вероятности двухфотонного процесса оже-типа от параметра ζ = mc / mv и частоты света (модель А)
81
§ 5.4. Уравнения баланса для заселённостей зон
Уравнения баланса для концентраций электронов nc , nc1 в двух зонах проводимости имеют следующий вид:
& |
= −Wc cnc |
|
(l ) |
j |
l |
fcc |
−γ |
(l ) |
j |
n−l |
nc |
− |
|
|
||||||||
nc |
+σcc |
|
|
|
|
|
|
|
||||||||||||||
1 |
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
−dc [( p0 + nc − n0 |
+ nc |
)nc |
− n0 p0 ], |
|
|
|||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
(5.26) |
|
& |
|
|
|
|
(l) |
j |
l |
fcc + 2γ |
(l ) |
j |
n−l |
nc |
+ |
|
||||||||
|
|
|
|
|
|
|||||||||||||||||
nc |
=Wc cnc1 −σcc |
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
+σ (n) jn (1− f |
)(1− f |
p |
) − d |
|
[( p |
+ n |
− n |
|
+ n |
)n |
− n p |
], |
||||||||||
vc |
c |
|
|
c |
|
|
|
0 |
c |
|
|
0 |
|
|
|
c |
c |
0 0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
с начальными условиями nc |
= 0, nc |
= n0 |
при t = 0. В формулах (5.26) Wc c – |
|||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
скорость релаксационных переходов электронов из верхней зоны проводимости в нижнюю, n0 и p0 – равновесные концентрации электронов в
нижней зоне проводимости и дырок в валентной зоне соответственно.
Скорости l-фотонных переходов w(l ) ≡σ (l ) jl между зонами проводимости c
cc1 cc1
и c1 описываются формулами, которые легко получить с помощью стандартной теории возмущений. Для случаев l = 3 и l = 2 получим:
|
|
|
|
|
4π 2e6 |
2m |
|
|
|
(3) |
|
|
p |
|
|
6 m |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
w(3) |
=σ |
(3) |
j3 = |
|
|
|
|
|
|
|
|
|
cr |
|
c1c |
|
|
cc1 |
|
|
cr |
, |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
cc1 |
|
cc1 |
|
|
|
|
|
6 |
8 |
|
10 |
|
3 |
3 2 |
(ω) |
|
|
|
|
|||||||||
|
|
|
|
|
|
πm |
h ω |
|
|
c εT |
|
|
|
|
||||||||||||||
|
|
|
|
64πe4 |
|
p |
|
|
2 [−2m |
|
|
|
(2) ]3 2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
wcc(2) =σcc(2) j |
2 = |
|
|
|
|
|
|
cc1 |
|
|
|
|
|
|
cr |
c1c |
|
j2 , |
(5.27) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
(ω)(hω) |
6 |
|
|||||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
m |
m c ε |
T |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
cr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(l ) |
= lhω − |
c c |
, m−1 |
= m−1 |
|
|
− m−1. |
|
|
|
|
||||||||||||||||
|
c c |
|
|
|
|
|
|
|
cr |
|
|
|
|
c |
|
|
|
c |
|
|
|
|
||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Cлагаемые, |
пропорциональные |
dc |
или dc, |
|
в правых частях (5.26) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
описывают обычную бимолекулярную рекомбинацию электронов в зонах проводимости с дырками в валентной зоне. Концентрация дырок определяется соотношением
p = nc |
− n0 |
+ nc + p |
0 , |
(5.28) |
|
|
1 |
|
|
причем p = p0 при t = 0.
При высоких интенсивностях света состояния вблизи дна зон проводимости c и c1 оказываются заполненными, а состояния близи потолка валентной зоны v опустошаются (т.е. возникает высокая концентрация дырок p). Это влияет на скорости прямых межзонных многофотонных переходов и непрямых многофотонных переходов оже-типа. Данные эффекты не являются критическими для рассматриваемой задачи. Тем не менее, их желательно учесть хотя бы в самом грубом приближении. С этой целью реальные распределения неравновесных электронов и дырок аппроксимируются
82
