
На величину модулей упругости, определяемых статическими методами (статическое, испытание обычно продолжается 5 ... 10 мин), оказывает влияние ползучесть материала (ползучесть – возрастание деформаций с течением времени при постоянном уровне напряжений; рис. 4.17: ε1 – мгновенная упругая деформация, εп – деформация ползучести в некоторый момент времени t*). Ползучесть приводит к кажущемуся снижению модулей Е и G (рис. 4.18), так как в опыте измеряются напряжение и деформация, соответствующие
точке 2, а не точке I;
E2 = tg 2 = / ( 1 + п ) E1 = tg 1 = / 1.
39

влияние ползучести
ε |
|
2 |
|
εп |
|
1 |
|
ε1 |
|
t* |
t |
Рис. 4.17 |
|
σ
1 |
2 |
|
|
α2 |
|
α1 |
|
|
ε1 |
εп |
ε |
|
|
|
|
Рис.4.18 |
|
У металлов ползучесть существенна лишь при высоких температурах, у высокополимерных материалов
(пластмассы, резина, каучук) ползучесть заметна и при комнатных температурах. 40
ε

При статических испытаниях "мягких" материалов (получающих большие деформации при малых нагрузках) трудно оставаться в пределах чисто упругой деформации без частичного перехода в пластическую область (рис. 4.19 точка 2); это ведет к кажущемуся снижению модулей E и G,
E2 = tg 2 E1 = tg 1.
2
σ
1
σпц
α2  α1
α1 

ε
Рис.4.19
41
От указанных недостатков свободны динамические методы в которых величины напряжений и деформаций и время протекания процессов весьма малы и поэтому не возникают пластические деформации и не успевают развиться деформации ползучести. Следовательно, динамические методы являются в принципе более точными, чем статические.
Существенные трудности возникают при использовании статических методов для определения модулей упругости весьма хрупких материалов, например, керамики, так как приходится измерять чрезвычайно малые перемещения.
Динамические методы определения модулей упругости основаны на связи последних со скоростью упругих волн, которая прямо или косвенно измеряется в исследуемом образце. 42
продольные и поперечные волны
Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
Упругими(или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению
распространения волны.
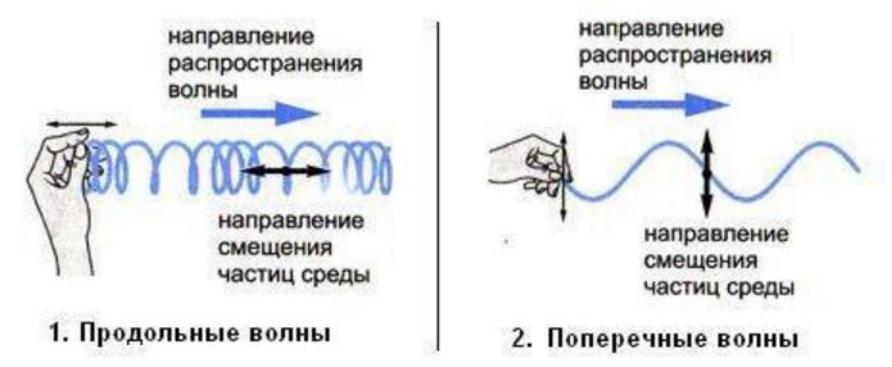
ПРОДОЛЬНЫЕ И ПОПОРЕЧНЫЕ ВОЛНЫ
Динамические методы определения модулей упругости можно разделить на методы, использующие непрерывные колебания, и импульсные методы. Среди первых наибольшее распространение получил резонансный метод, основанный на использовании явления резонанса в исследуемом образце, совершающем вынужденные механические колебания. Резонанс возникает при совпадении частоты вынуждающей силы с одной из частот собственных колебаний образца и характеризуется максимальной амплитудой колебаний. Обычно испытанию подвергаются образцы материала в виде тонкого призматического стержня.
45

Функциональная схема прибора типа "Звук"
генератор
 излучающий преобразователь
излучающий преобразователь
образец
насадка
приемный
преобразователь
усилитель индикатор
Рис. 4.20
46

ОПРЕДЕЛЕНИЕ МОДУЛЕЙ УПРУГОСТИ МАТЕРИАЛА ИМУЛЬСНО-ФАЗОВЫМ МЕТОДОМ
Рис. 4.21 |
47 |
|

Вращением микрометрического винта оператор может менять расстояние между пьезопластинами жидкостной эталонной линии, при этом имеется возможность совместить оба высокочастотных импульса на экране прибора. В момент совмещения, которое означает, что время прохождения сигнала через эталонную и измерительную линии одинаково, берется отсчет по шкале микрометра. Таких отсчетов делают два: первый – без образца в измерительной линии (n1) , второй – с образцом (n2). Время прохождения ультразвукового импульса в образце будет равно времени прохождения импульса в столбе
эталонной жидкости высотой (n2 – n1): ,
t = l = n2 −n1 v vж
где vж – скорость ультразвука в эталонной жидкости; l – длина образца; v – искомая скорость ультразвука в образце. 48
