8.3 Контрольные вопросы

1. Какие напряжения возникают при чистом изгибе?

2. Сформулируйте условие прочности при изгибе.

3. Сформулируйте условие жесткости при изгибе.

4. Как распределяются по сечению напряжения при изгибе?

5. Чему равны нормальные напряжения на нейтральной линии?

6. Как определить максимальные нормальные напряжения при изгибе в се­чении и по длине балки?

7. Запишите правило знаков для построения эпюры поперечных сил.

8. Запишите правило знаков для построения эпюры изгибающих моментов.

9 Сложное сопротивление. Расчеты на прочность

9.1 Основные определения и положения

В общем случае в различный точках балки, нагруженной произволь­ными силами, возникают различные нормальные касательные напря­жения. Их совокупность характеризует напряженное состояние в точке.

Для практических расчетов сложное напряженное состояние заме­няют эквивалентным ему равноопасным одноосным растяжением с экви­валентным напряжением .

Условие прочности в этом случае выглядит следующим образом:

. (9.1)

Для определения пользуются различными теориями прочности:

- 3-я теория прочности - теория наибольших касательных напряже­ний - записывается уравнением

; (9.2)

- 4-я теория прочности - энергетическая теория - записывается урав­нением

(9.3)

9.2 Расчетно-графическая работа № 6 «Расчет вала на прочность при совместном действии кручения и изгиба»

Проверить прочность вала, испытывающего совместное действие кручения и изгиба, на статическую прочность при кратковременных пере­грузках в целях предотвращения пластических деформаций. Схему вала, схему сил в зацеплении косозубого зубчатого колеса (F_t F_r, F_a), нагрузку на вал со стороны ременной передачи F_e, значения необходимых для рас­чета параметров берем из таблиц 9.1, 9.2, 9.3 и 9.4.

Силы в зацеплении зубчатого колеса рассчитываются по зависимостям: -радиальная, - осевая, где - угол зацепления, угол наклона зуба.

Крутящий момент T, передаваемый валом, определяется по формуле

(9.4)

где d₁ - делительный диаметр зубчатого колеса, м.

Допускаемые напряжения , где - предел текучести материала вала.

Таблица 9.1 - Схемы валов для расчетно-графической работы №6

Таблица 9.3 - Нагрузка на вал со стороны ременной передачи для расчетно-графической работы №6

Таблица 9.4 - Значения параметров для расчетно-графической рабо­ты №6

Но­мер вари­анта	Окружная сила Ft,кН	На­грузка навал Fb,kH	Делит, диам. зуб. кол. d1MM	Диа­метр вала d, мм	а, мм	мм	с, мм	Коэф. пере­грузки, кп	Предел теку­чести , МПа
0	3	0,5	200	50	60	100	50	1,4	270
1	5	0,6	220	55	70	120	60	2,5	290
2	7	0,7	240	60	80	140	70	1,6	310
3	9	0,8	260	65	90	160	80	1,8	330
4	11	0,9	280	70	100	180	90	2	350
5	13	1	300	75	110	200	100	2,2	340
6	15	1,1	270	80	120	220	95	2,4	320
7	17	1,2	250	83	130	230	85	2,6	300
8	12	1,3	230	85	140	240	75	2,8	280
9	8	1,4	210	88	150	250	65	3	260

Решение

1. Составляем расчетную схему вала (рис. 9.1, б).b

2. Строим эпюру крутящего момента Т (рис. 9.1, в).

На всей длине вала СД действует крутящий момент Т= 2800 .

3. Исходя из принципа независимости действия сил, рассматриваем схему вала в двух плоскостях: в вертикальной плоскости XOY (рис. 9.1, г) и в горизонтальной плоскости XOZ (рис. 9.1, е).

4. Определяем реакции R_Ay и R_By в опорах А и В, действующие в вер­тикальной плоскости (рис. 9.1, г). Принято силы F_r и F_a рассматривать в одной плоскости.

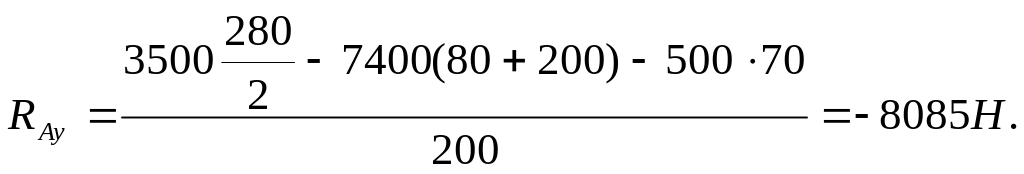
Отрицательный знак реакции R_Ay означает, что она направлена в

противоположную сторону. Поэтому на расчетной схеме исправляем ее направление.

Выполним проверку:

Равенство выполняется, реакции найдены верно.

5. Определяем реакции R_Az и R_Bz в опорах А и В, действующие в го­ризонтальной плоскости (рис. 9.1,е):

Выполним проверку:

Равенство выполняется, реакции найдены верно.

Рисунок 9.1 - Построение эпюр к РГР №6

6.Строим эпюру изгибающих моментов в вертикальной плоскости (рис. 9,1, д). Балку делим на три участка СА, АВ и ВД. Для этих участков берем сечения х₁ х₂, х₃ и составляем уравнения изгибающих моментов, по которым строим эпюру.

Участок СА

при

при

Участок АВ

при х₂ = а;

при х₂ = а + b;

Участок ВД

при

при х₃ = с;

7. Строим эпюру изгибающих моментов в горизонтальной плоскости (рис. 9.1, ж).

Участок СА

при х₁ = 0;

при х₁ = а;

Участок АВ

при х₂ = а;

при х₂ = а + b;

Участок ВД

8. Строим суммарную эпюру изгибающих моментов (рис. 9.1, з). Для этого определяем значения суммарного изгибающего момента в точках А, В, С и Д по зависимости

точка С,

точка А,

точка В,

точка Д,

Причем если на одной из эпюр в какой-либо точке был скачок, то в этой точке нужно считать дважды по двум точкам в месте скачка та­ким образом, чтобы на эпюре также получился скачок.

9. Из анализа эпюр (рис. 9.1, в, з) видно, что наиболее опасным явля­ется сечение в точке А. В этой точке действует максимальный суммарный изгибающий момент и крутящий момент Т = 2800 Н • м. Сечение вала в точке А находится в сложном напряженном состоянии. Эквивалентное напряжение в этом сечении определяем по четвертой теории прочности

где - максимальное нормальное напряжение, возникающее

от изгиба вала;

- максимальное касательное напряжение, возникающее от кручения;

W_z - осевой момент сопротивления сечения вала, который для кругло­го вала равен

W_z = 0,1d³ = 0,1 • 50³ = 12500 мм³;

W_p - полярный момент сопротивления сечения вала, который для круглого вала равен:

W_z = 0,2d³ = 0,2 • 50³ = 25000 мм³;

Эквивалентное напряжение с учетом перегрузок

Для статической прочности вала при кратковременной перегрузке должно выполняться условие

где

Таким образом, условие статической прочности вала при кратковре­менной перегрузке выполняется.