9.4 Методы интегрирования
1. Табличное интегрирование
Чтобы приступить к действию интегрирования, необходимо наизусть знать
таблицу производных и интегралов.
Примеры:
1)
;
2)
;
3)
.
2. Метод подстановки
Метод подстановки, или замена переменной в неопределенном интеграле состоит в том, чтобы в подынтегральной функции ввести новую переменную с целью привести исходный интеграл к табличному варианту.
Примеры:
1)
;
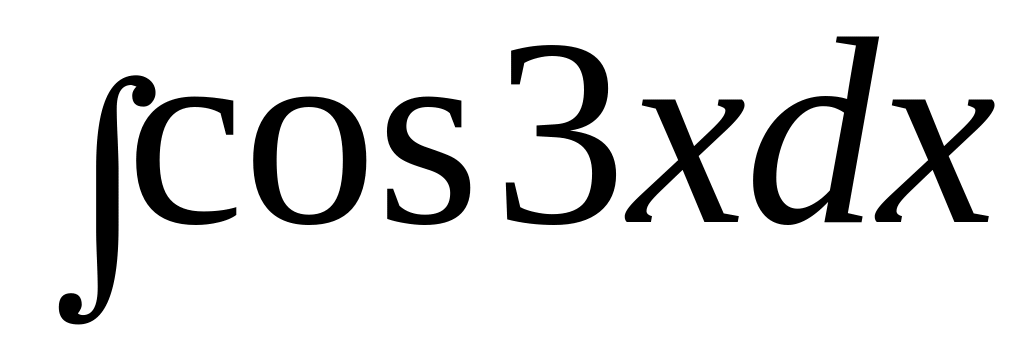2)
;
3)
;
3)
;
4)
;
5)
.
Подведение под знак дифференциала
по существу равносильно применению свойства 5 независимости интеграла от переменной интегрирования. Суть в том, чтобы в интеграле перейти к другой переменной (t), относительно которой интеграл становится табличным.
Примеры.
1)
;
2)
;
3)
;
4)
;
5)
.
3. Интегрирование по частям
Интегрирование по частям состоит в том, что подынтегральное выражение представляется каким-либо образом в виде произведения двух сомножителей u и dv, затем после нахождения du и v используется формула интегрирования по частям:
Пример 1. Найти
=
=
.
При выборе обозначения сомножителей обычно за dv выбирают сомножитель, который легко интегрировать, оставшиеся сомножители обозначают за u.
Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
Пусть Р(х) – многочлен, k – число.
1) В интегралах вида:
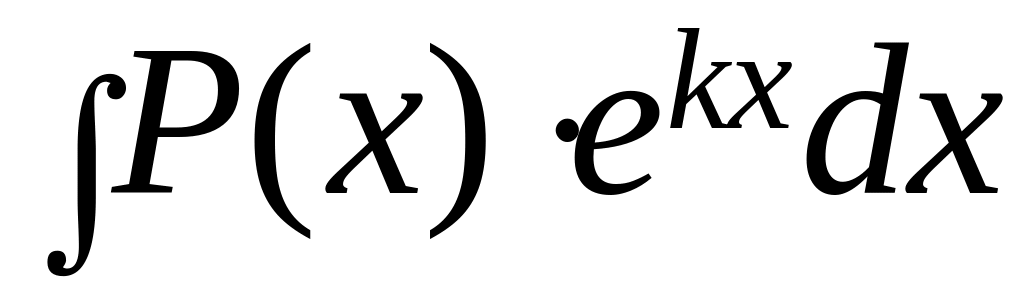
обозначим:
за u = P(x), за dv - остальные множители.
2) В интегралах вида:
;
;
;
обозначим:
dv = P(x)dx, u - остальные множители.
3) В интегралах вида:
,
где a и b - числа
обозначим:
u = еах, dv - остальные множители.
Пример 2. Найти
интеграл
.
Решение.
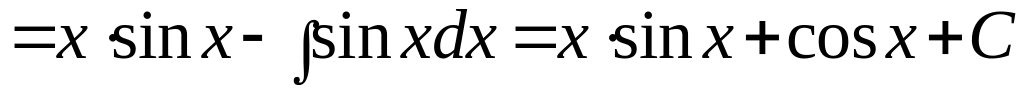
Пример 3. Найти
интеграл
.
Решение.
Пример 4. Найти
интеграл
.
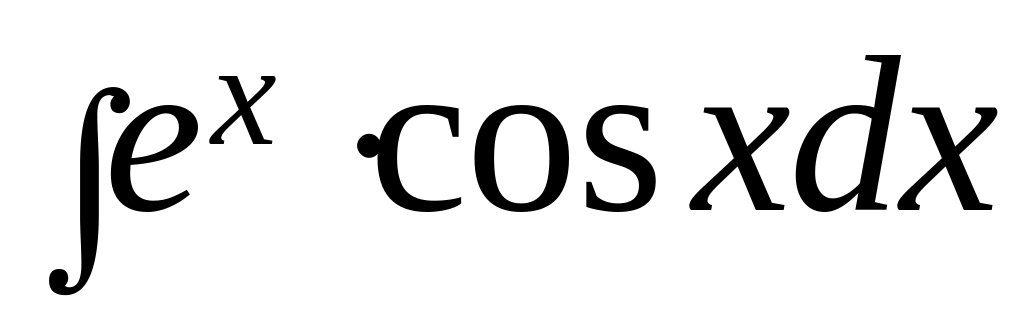Решение.
.
;
;
.
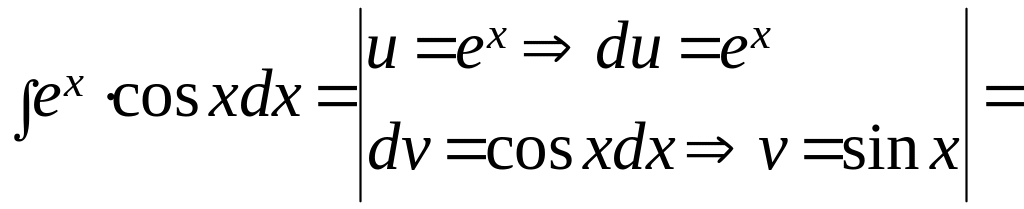
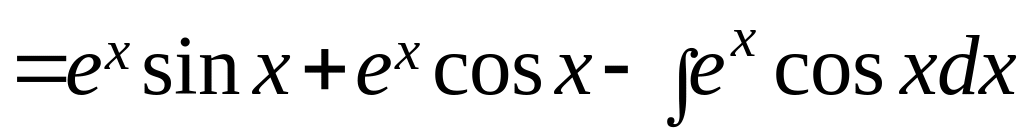9.6. Интегрирование различных классов функций.
9.6.1. Интегрирование рациональных функций
А) Простейшими дробями называются следующие дроби: (пусть А, В, a, k – числа )
(I
типа),
(II
типа, если k
> 1 – целое),
(III
типа, если D=
b2
– 4ac
< 0),
(IV
типа, если k
> 1, D
< 0).
Б) Рациональной функцией (дробью)
называется отношение двух многочленов
;
если n < m, то дробь называется правильной,
если n > m, то дробь называется неправильной.
Теорема. Каждая неправильная рациональная дробь равна сумме многочлена и правильной дроби.
= f(x)
+
Пример.
Разложить на простейшие дроби
неправильную рациональную дробь
.
РЕШЕНИЕ. Выделим целую часть делением числителя на знаменатель:
Теорема. Правильная рациональная дробь представляется единственным образом в виде суммы простейших дробей.
● Разложение правильной дроби на сумму простейших дробей выполним по правилам:
1) если в знаменателе рациональной дроби различные действительные корни, то
.
2) если в знаменателе рациональной дроби п одинаковых действительных корней, то
.
3) если в знаменателе рациональной дроби комплексные корни (D < 0), то
.
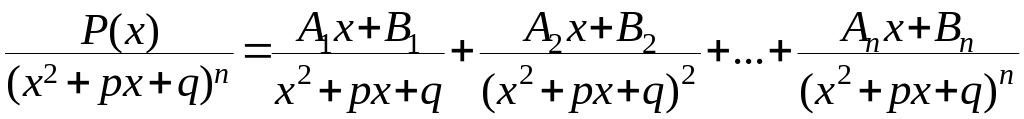Неизвестные коэффициенты числителей (А, В, ...) вычисляются методом неопределенных коэффициентов.
Пример. Найти интегралы.
а)
;
б)
.
Решение.
а) =
Выполним разложение дроби на простые дроби:
=
;
Приравниваем числители дробей левой и правой частей равенства.
* 3х2 + 2х – 3 = А(х2 – 1) + В(х2 + х) + С(х2 – х)
Приравниваем коэффициенты равенства (*) при одинаковых степенях:
→
2В = 2, В = 1, С = – 1.
=
;
.
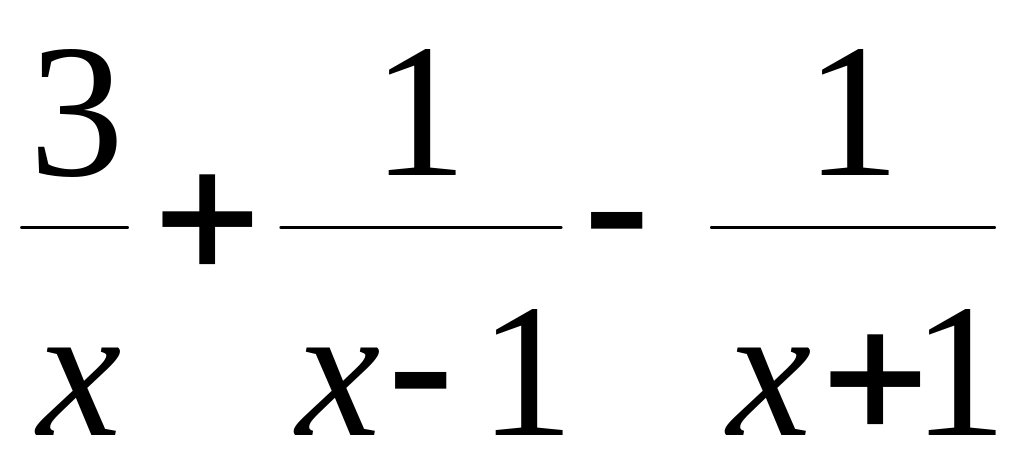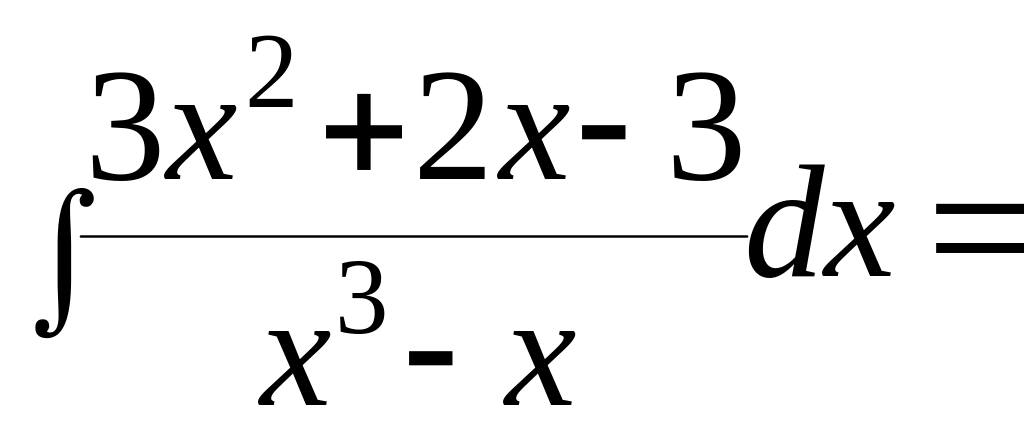
б) Решение.
=
Разложим на простейшие дроби:
=
;
* х – 4 = А(х – 3) + В(х –2 ;
Подставим корни знаменателя в равенство *
если х = 2, то 2 – 4 = А(2 – 3) + В(2 –2 );
– 2 = – А; А = 2;
если х = 3, то 3 – 4 = А(3 – 3) + В(3 –2 );
– 1 = В; В = – 1.
.
Примеры: