8 Комплексные числа и действия над ними

Извлечение корня из отрицательного числа – невыполнимая операция на множестве действительных чисел. Значит есть потребность в дальнейшем расширении понятия числа – эти числа назвали комплексные числа. Они введены в алгебру в середине 16-го века, с конца 17-го века они применяются и в анализе.

8.1. Алгебраическая форма комплексного числа и его геометрическое изображение.

Определение. Комплексным числом называется упорядоченная пара (х, у) действительных чисел, которую можно записать выражением

z = х + i у,

где х и у – действительные числа,

i - мнимая единица, i ² = - 1 , 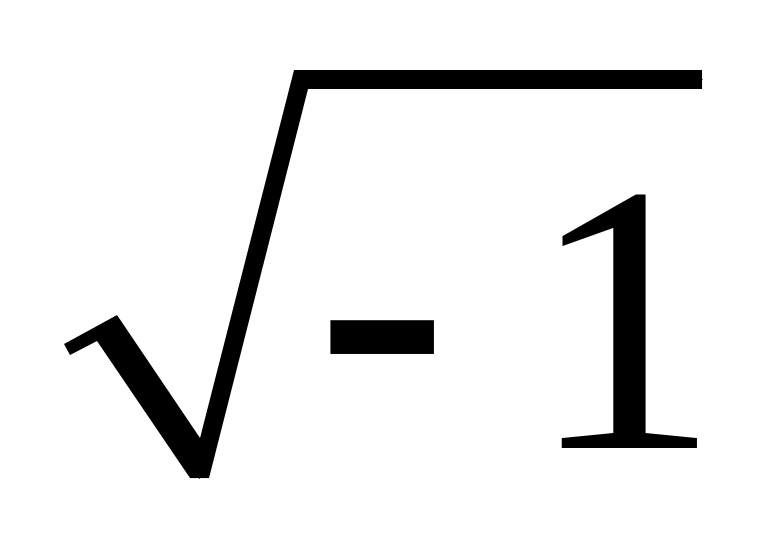= i.

х – действительная часть к.ч. (Re z),

у – мнимая часть к.ч. (Im z).

Обозначение i для мнимой единицы ввел Леонард Эйлер в 1777 году. Математик, физик, механик, астроном – он родился в Швейцарии в 1707 году и окончил Базельский университет в 1724 году. По приглашению Петербургской Академии приехал в Россию в 1727. До конца жизни с небольшим перерывом он работал в Петербурге.

ПРИМЕР 1. Решить уравнение х² + 4 = 0.

РЕШЕНИЕ. х² = - 4 ,

.

ОТВЕТ: х₁ = 2 i , х₂ = - 2 i.

Алгебраическая запись комплексного числа

z = х + iу,

х = Re z - действительная часть к. ч.,

у = Im z - мнимая часть к .ч.

если х = 0, то число i у – чисто мнимое,

если у = 0, то число отождествляется с действительным числом.

– сопряженные числа

(отличаются знаком мнимых частей).

На плоскости зададим прямоугольную декартову систему координат.

Комплексному числу z = х + i у ставим в соответствие точку М этой плоскости с координатами (х, у), вследствие этого:

Ох - действительная ось,

Оу - мнимая ось.

Всякое комплексное число z = х + i у можно изображать радиус-вектором .

модуль комплексного числа:

r =│z│= (длина вектора)

аргумент комплексного числа:

Arg z = φ = (угол радиус-вектора)

Аргумент комплексного числа z = 0 не определен.

Аргумент комплексного числа z ≠ 0 величина многозначная и определяется с точностью до слагаемого 2πκ, где κ – целое число.

Главное значение аргумента заключено в промежутке (-π, π].

8.2 Формы записи комплексных чисел.

1) Алгебраическая форма

z = x + iy.

2) Тригонометрическая форма

z = r (cos φ + i sin φ).

3) Показательная форма

z = re^{i φ}.

ПРИМЕР .Записать число z = -1 + i в тригонометрической и показательной формах.

РЕШЕНИЕ.

1) Найдем модуль к.ч.: имеем х = -1, у = 1,

тогда .

2) Найдем аргумент к.ч. :

φ = , т.к. вектор во 2-ой четверти.

3) Тригонометрическая форма

z = - 1 + i =

4) Показательная форма - 1 + i = .

8.3 Действия над комплексными числами.

Все арифметические операции над комплексными числами определяются из правил сложения и умножения многочленов (x₁ + iy₁) и (x₂ + iy₂) , считая i ² = - 1.

Рассмотрим действия над комплексными числами z₁ = x₁ + iy₁ и z₂ = x₂ + iy₂.

1) Сложение двух комплексных чисел

z₁ + z₂ = (x₁ + x₂) + i (y₁ +y₂)

2) Вычитание двух комплексных чисел

z₁ - z₂ = (x₁ - x₂) + i (y₁ -y₂)

3) Произведение двух комплексных чисел z₁z₂ = (x₁x₂ – y₁y₂) + i (x₁y₂ + x₂y₁)

4) Частное двух комплексных чисел (домножить числитель и знаменатель на число сопряженное знаменателю и выполним преобразования, учитывая, что i ² = - 1)

ПРИМЕР. Найти сумму, разность, произведение и частное комплексных чисел

z₁ = 5 + i и z₂ = 2 + 3i.

Решение.