
- •1. Основные понятия и аксиомы статики.
- •33. Законы Галилея-Ньютона.
- •39. Элементарный и полный импульс силы.
- •40. Теорема об изменении количества движения точки.
- •41. Количество движения системы. Теорема об его изменении.
- •53.Теорема об изменение кинетического момента и ее следствия.
- •59.Принцип возможных перемещений.
- •60.Общее уравнение динамики.
1. Основные понятия и аксиомы статики.
Статика – это раздел теоретической механики, в котором рассматривают операции преобразования систем сил в системы, им эквивалентные, и изучают условия равновесия материальных тел под действием сил.
Сила – это векторная величина, являющаяся мерой механического действия одного материального тела на другое.
Мат. точка – тело обладающее массой и не имеющее объём.
Мех. система – такая савокупность мат. точек, в которой положение и движения каждой точки зависят от положения и движения других.
Система сил – савокупность нескольких сил действующих на объект.
Равнодействующая сила – эквивалентная системе сил.
Уравновешивающая сила – эквивалентная равнодействующей и направленная противоположной.
Уравновешенная система сил – система эквив. нулю.
Абсол. твёрд. тело – расстояние между любыми точками которое остаётся постоянным.
Аксиомы статики – это законы, установленные непосредственными наблюдениями и опытной проверкой следствий, логически вытекающих из аксиом.
1) Система двух сил, действующих на свободное твердое тело, является уравновешенной тогда и только тогда, когда эти силы равны по модулю и действуют вдоль одной прямой в противоположные стороны.
2) Если к данной системе сил добавить или отнять от нее уравновешенную систему сил, то полученная система сил будет эквивалентна исходной.
3) Система двух сил, приложенных к телу в одной точке, имеет равнодействующую, приложенную в той же точке и равную геометрической сумме сил.
4) Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.
5) Равновесие изменяемого (деформируемого) тела не нарушится, если тело станет абсолютно твердым.
6) Если на тело не действуют силы или действует уравновешенная система сил, то оно сохраняет состояни покоя или равномерно прямолинейного движения.
3. Система сходящихся сил. Условия равновесия.
Силы линии действия которых пересекаются в одной точке образуют ССС. Для равновесия ССС необходимо и достаточно равенство 0 Равнодействуюшей силы. R = 0
4. Алгебраический и геометрический момент силы относительно центра
Алгебраическим моментом силы относительно центра называется- взятая со знаком + или – произведение модуля силы на плече. Плече это перпендикуляр проведенный из центра на линию действия силы. Вектор момент силы определяется формулой М=r*F и направлен перпендик. К плоскости проходящей через r, F направлен в ту сторону откуда кратчайший поворот от r к F против часовой стрелки.
5. Момент силы относительно оси
Чтобы найти момент силы относительно оси надо спроектировать на плоскость перпендикулярно этой оси и модуль перпендик. Умножить на плечо это перпендикуляр проведенный из точки пересечения оси к плоскости на линию действия силы M=Fxyh1 М=0 если сила паралельна оси, линия действия пересекает ось.
6. теория пар сил
Две силы равные по модулю противоположного направления и нележашие на одной прямой образуют пару сил.
7. Лемма пуансо
Действие силы Р, приложенной к точке тела не изменится, если эту силу перенести || в любую точку О этого тела – центр приведения, добавив пару сил с моментом, равным моменту силы Р относительно центра приведения.
8. Основная теорема статики
заключается в том что любую произвольную систему сил можно заменить более простой эквивал. состоящей из одной силы – главного вектора и одной пары сил – главного момента.
9. Теорема вариньона о моменте равнодействующей
Если система сил приводится к равнодействующей то момент равнодействующей относительно точки на плоскости равен алгебраической сумме равен моменту сил M0(F)=M(F|)+M(F||)
10. Условия равновесия произвольной системы сил
Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на оси декартовой системы координат равнялись нулю и суммы моментов всех сил относительно этих осей также равнялись нулю.
11. Центр паралельных сил Центр тяжести твердого тела и его координаты. Способы определения центра тяжести.
Точка
прилож. равнодействуюшей системы || сил
при любых поворотах их в одну сторону
и ту же сторону на один и тот же угол
называется центром паралельных сил.
Центр тяжести твердого тела точка
приложения равнодействующих сил тяжести
всех точек тела при любых поворотах
тела в пространстве. Координаты:
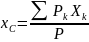
12. трение скольжения
Сила трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении.
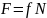
13. Трение качения
Трение качения — сопротивление движению, возникающее при перекатывании тел друг по другу т.е. сопротивление качению одного тела (катка) по поверхности другого.
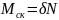
1)
гладкая поверхность
 2)
гибкая связь
2)
гибкая связь

3)
неподв. цилинд. шарнир
 4)
подвиж. цилинд. шарнир
4)
подвиж. цилинд. шарнир
5)
линейный невесомый стержень
 6)
жёсткая заделка
6)
жёсткая заделка

7)
сферический шарнир

14. векторный способ задания движения точки U и a
Для
задания движения надо знать r=r(t)
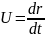 ;
;

15. координатный способ задания движения точки
Для
задания движения этим способом надо
знать координаты точки как ф-ции времени.
x=f1(t).
y=f2(t),
z=f3(t),
Ux=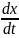 ; Uy=
; Uy=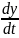 ; Uz=
; Uz=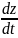 ax=
ax=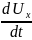 ; ay=
; ay= ;
az=
;
az=
16. Естественный способ задания движения точки
Для
задания движения этим способом надо
знать траекторию движения начало отсчета
с указанием + и – направления движений
и закон движения по этой траектории.
aτ=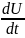 ; an=
; an=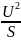 ;
a=
;
a=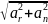 ;
ar точки характеризует изменение U.
;
ar точки характеризует изменение U.
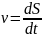
17. Частные случаи движения точки
Равномерное движение S=S0 + Ut
Равнопеременное
движение U=U0+art;
S=S0
+ U0t+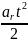 .
.
ar=0 an=0 равном. прямолинейн.
ar≠0 an=0 равном. прямолинейн.
ar=0 an≠0 равном. кривол.
ar≠0 an≠0 равном. кривол.
18. Поступательное движение тела
Поступательное движение — это механическое движение системы точек (абсолютно твёрдого тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени. При поступательном движении тела U всех его точек равных по величине и направлению, ускорение их так же = м/у собой и все точки имеют одинаковые траектории.
19. Вращательное движение тела угловая скорость угловое ускорение
Это
движение тела при котором любые две
точки связаные с телом неподвижны и
через них проходит ось вращения тела,
а все остальные точки описывают окружность
с центром на этой оси
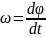 - углов. скорость.
- углов. скорость.
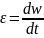 - угл ускор
- угл ускор
20. ускорение точки вращающегося тела
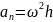 - норм. ускорен.
- норм. ускорен.
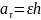 - кас. ускор
- кас. ускор

21. векторные формулы скорости и ускорения точек вращающегося тела
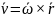 – формула Эйлера,
r
– радиус-вектор.
– формула Эйлера,
r
– радиус-вектор.
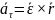 – векторн. кас.
ускор.
– векторн. кас.
ускор.
 – векторн. норм.
ускор.
– векторн. норм.
ускор.
22. частные случаи вращательного движения тела
1) равномерное вращение
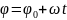
2) равнопеременное вращение
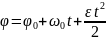
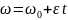
23. плоско-параллельное движение тела
плоско-параллельным движение называется движение тела параллельно неподвижной плоскости.
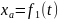

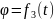
24. теорема о сложении скоростей точки при плоском движении тела
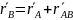
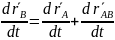
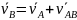 – теорема
– теорема
скорость любой точки тела при плоском движении равна геом. сумме скорости полюса и скорости точки при повороте вместе с телом вокруг полюса.
26. теорема о проекциях скоростей
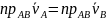
проекции скоростей двух точек одного звена на направление отрезка их соединяющего равны между собой.
27. мгновенный центр скоростей (МЦС) и док-во его существования
МЦС называется точка неизменно связана с телом скорость которой в данный момент = 0.
док-во:
пусть известна скорость полюса
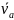 и
и
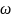 тела, восстановим к
тела, восстановим к
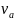 перпендикуляр, применим для точки P
теорему о скоростях
перпендикуляр, применим для точки P
теорему о скоростях
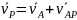
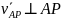
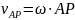
можно
подобрать такое AP
чтобы:
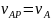 ;
;
 →
→
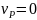
28. способы определения положения МЦС.
1)
МЦС находится на перпендикуляре
восстановленным к скорости полюса
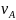 на расстояние
на расстояние

2) если известны направленичя скоростей двух точек одного звена и модуля одной из скоростей, то МЦС находится на пересечение перпендикуляров, восстановленных к началам скоростей этих точек.
29. сложное движение точки.Теорема о скоростях.
Если точка одновременно участвует в двух или более движениях, то ее движение называется сложным.
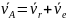
абсолютная скорость точки в сложном движение равна геометрической сумме ее относительной и переносной скоростей.
30. теорема о сложнии ускорений в сложном движении точки (переносное поступательное движение).
абсолютное ускорение точки при переносном поступательном движении равно геометрической сумме относительного и переносного ускорения
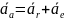
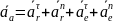
31.теорема Кориолиса.
абсолютное ускорение точки при переносном непоступательном движении равно геометрической сумме относительного, переносного и кориолисного ускорений.
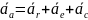

32. величина и направление ускорения Кориолиса.
 -величина
-величина
способы определения направлений:
1)по
правилу векторного произведения, вектор
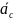 направлен ⊥
плоскости проходящей через
направлен ⊥
плоскости проходящей через
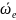 и
и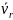 в ту сторону чтобы глядя ему навстречу
от
к
видеть против часовой стрелки.
в ту сторону чтобы глядя ему навстречу
от
к
видеть против часовой стрелки.
2) правило Жуковского. Для определения направления надо спроектировать на плоскость ⊥ оси переносного вращенияя и полученную проекцию поверну в этой плоскости на 900 в сторону вращения.
